4. Преобразование случайной величины

В блоках радиоэлектронных устройств сигнал может подвергаться различным преобразованиям. Так же преобразуется шум, при этом изменяется закон его распределения. Задача формулируется так [2]: случайная величина с плотностью распределенияпреобразуется:

;

найти плотность распределения . Если существует обратное преобразование

, (5)

общее решение [2]

- (6)

- произведение абсолютного значения производной обратной функции (5) и исходной плотности, в которой аргумент заменяется по формуле (5).

Пример 3. Пусть ,. Найти. Решение задачи по формулам (5) и (6):

, , . (7)

Так как , искомую плотность можно записать

, .

Решения подобных задач полезно проверять: нормирована ли ?

syms x

f=1/2/sqrt(2*pi*x)*exp(-x/2)

F=int(f)

ezplot(F,0,10)

ylim([0 0.5])

Эта программа позволит определить, выполняется ли равенство (рис. 5)

.

Ясно, что нормировка требует умножения на 2:

.

Это связано с тем, что формальный расчет (7) не учитывал половину исходных значений .

Рис. 5. К расчету плотности распределения

Варианты задания

1. Статистика , независимые,,

. Проверить гипотезу H: ,,.

2. Статистика . Проверить гипотезуH: .

3. Статистика . Проверить гипотезуH: .

4. Проверить гипотезу о величине , генерируемой функциейRAND:.

5. Распределение Релея: ,,инезависимы;. Проверить гипотезу.

6. Распределение Максвелла: ,,,,,независимы;.

Проверить гипотезу .

7. Проверить гипотезу о величине , генерируемой функциейRANDN: .

8. Распределение арксинуса: ,.

Проверить гипотезу :

9. Показательное распределение: ,,инезависимы;

. Проверить гипотезу :,.

10. - распределение: независимые,;

, ,.

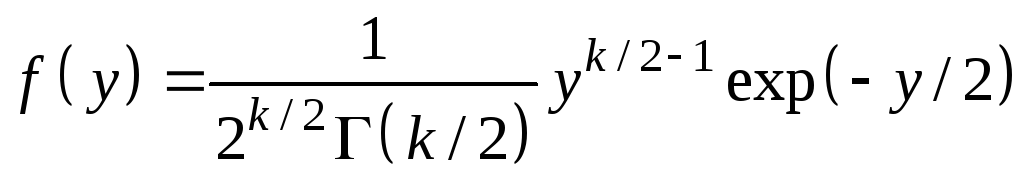Проверить гипотезу для одной степени свободы ():

.

Гамма- функция вычисляется функцией. Частные случаи:,,,,

11. Проверить гипотезу для- распределения с двумя степенями свободы (, экспоненциальное распределение):

.

12. Проверить гипотезу для- распределения с четырьмя степенями свободы ():

.

13. Гамма – распределение:

.

При - целом это распределение называется распределением Эрланга порядка, описывающим сумму независимых случайных величин с распределением

.

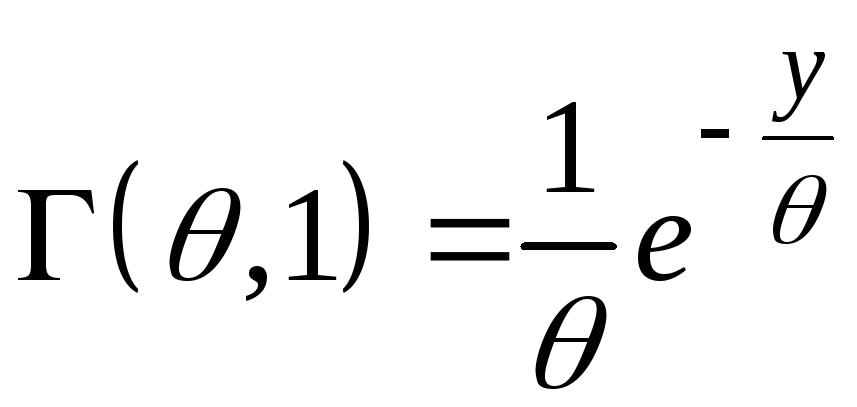Проверить гипотезу о распределении Эрланга с двумя степенями свободы.

14. Проверить гипотезу о распределении Эрланга с тремя степенями свободы.

15. Проверить гипотезу о том, что гамма – распределение есть- распределение сстепенями свободы для случая.

16. Распределение Стъюдента: ,,инезависимы;

. Проверить гипотезу :

, .

17. Распределение Фишера (Снедекора): ,,инезависимы;. Проверить гипотезу:

, .

18. Нецентральное - распределение сстепенями свободы имеет плотность

,

- параметр нецентральности. Оно описывает сумму независимых величин

, - сумма квадратов математических ожиданий.

Проверить гипотезу о нецентральном - распределении с одной степенью свободы и параметром нецентральности.

19. Проверить гипотезу о нецентральном - распределении с тремя степенями свободы; параметр нецентральностизадать самостоятельно.

20. Проверить гипотезу о нецентральном - распределении с пятью степенями свободы; параметр нецентральностизадать самостоятельно.

21. Проверить гипотезу о нецентральном - распределении с двумя степенями свободы

,

- гиперболический косинус. Параметр нецентральности задать самостоятельно.

22. - мерный случайный вектор. Задана квадратичная форма

.

Проверить гипотезу о том, что величина для случая ; вектор среднихи корреляционную матрицузадать самостоятельно.

23. Выборочное среднее , независимые. Задана статистика .Проверить гипотезу :. Параметры,,задать самостоятельно.

24. Выборочня дисперсия 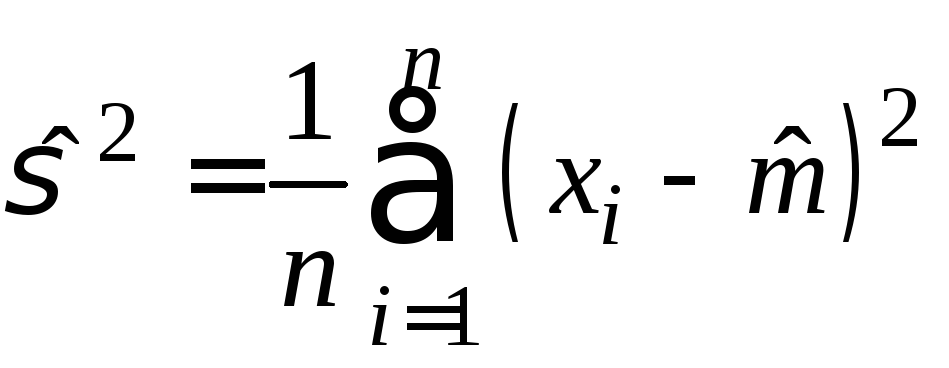, независимые. Задана статистика 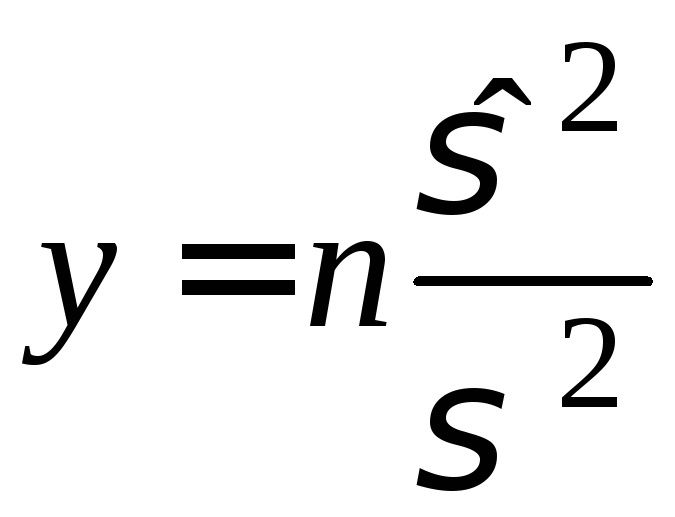.Проверить гипотезу :. Параметры,,задать самостоятельно.

25. Статистика , независимые,.Проверить гипотезу H: .

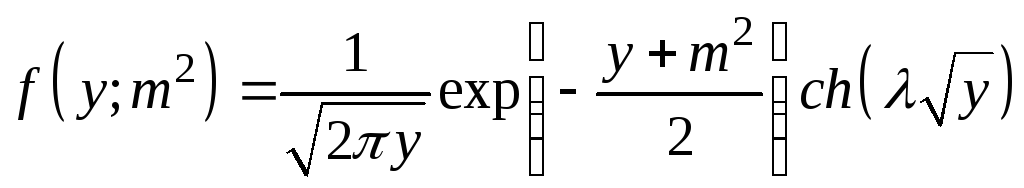MATLAB – функции:

NORMCDF(X,M,SIGMA) – нормальное распределение;

UNICDF(X,A,B) – равномерное распределение от A до B;

RAYLCDF(X,B) – распределение Релея с параметром B =;

EXPPDF(X,MU) – показательное распределение с параметром(плотность распределения);

CHI2CDF(X,V) - - распределение сVстепенями свободы;

NCX2CDF(X,N,L) – нецентральное - распределение с степенями свободы и параметром нецентральностиL;

TCDF(X,V) - распределение Стъюдента сVстепенями свободы;

FCDF(X,K1,K2) - распределение Фишера сK1 иK2 степенями свободы.

Пример. Статистика . Проверить гипотезуH: .

Программа

N=5000

del=0.5

x=-3:del:3;

f=normpdf(x,0,1)

y=randn(1,N);

H=hist(y,x)

hh=hist(y,x)/N/del % гистограмма для рисунка

h=hist(y,x)/N % гистограмма для расчета вероятностей

plot(x,f)

hold on

stem(x,hh)

рассчитывает теоретическую плотность распределения и

гистограмму (рис. 1).

Рис. 1. Плотность распределения и гистограмма

Расчеты вероятностей попадания в интервалы дискретизации должны выполняться с функцией . Применение функциитребует сдвига на полинтервала:

F=normcdf(x+del/2,0,1) % сдвиг на полинтервала

p=diff(F)

ppp=sum(p)

pp=sum(h)

dH=diff(cumsum(h))

n=length(dH)

P=[p;dH]

0.0092 0.0278 0.0656 0.1210 0.1747 0.1974 0.1747

0.0106 0.0276 0.0620 0.1168 0.1732 0.2036 0.1752

0.1210 0.0656 0.0278 0.0092 0.0024

0.1194 0.0674 0.0284 0.0092 0.0032

Критерий :

hi=N*sum((p-dH).^2./p)

hi0=chi2inv(0.95,11)

дает результат = 5.4804 при критическом значении19.6751. Гипотеза не отвергается.

Пример расчета вероятности попадания величины, распределенной по закону Максвелла, в интервал (a,b).

syms x

f=sqrt(2/pi)*x^2*exp(-x^2/2) % плотность Максвелла

F=int(f) % функц. распред. Максвелла

ezplot(F,0,4)

a=1

b=1.5

p=int(f,a,b) % вероятность попадания в интервал (a,b)

p = (7186705221432913/18014398509481984*2^(1/2)*erf(3/4*2^(1/2))-7186705221432913/18014398509481984*2^(1/2)*erf(1/2*2^(1/2)))*pi^(1/2)-21560115664298739/18014398509481984*exp(-9/8)+

+7186705221432913/9007199254740992*exp(-1/2) = 0.2791.

Литература

1. Соколов Г.А, Гладких И.М. Математическая статистка. - М.: Экзамен, 2007. –

431 с.

2. Ивченко Г.И., Медведев Ю.И. Математическая статистика. - М.: Высшая школа, 1984. – 248 с.

3. Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1982. – 256 с.

Лабораторная работа № 2

ГЕНЕРАТОР ВЕКТОРНЫХ РЕАЛИЗАЦИЙ

СЛУЧАЙНОГО ПРОЦЕССА

Цель работы: освоение аппарата сингулярного разложения корреляционной матрицы для генерирования псевдослучайных векторов с заданными корреляционными свойствами.