МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО

ОБРАЗОВАНИЯ

Санкт - Петербургский

государственный университет аэрокосмического приборостроения

-------------------------------------------------------------------------------------------------

МОДЕЛИРОВАНИЕ СИСТЕМ

Методические указания

к выполнению лабораторных работ

Санкт - Петербург

2006

Лабораторная работа № 1

Оценка закона распределения

1. Гипотеза о законе распределения случайной величины

Критерий согласия – в математической статистике классическое название правила проверки гипотезы о законе распределения случайной величины [1]. Общее решение множества задач математической статистики формулируется так: по наблюдениям необходимо сформировать статистику (число)

, (1)

которое позволит получить решение поставленной задачи. Например, в задаче проверки гипотезы о входном сигнале против альтернативыформируется статистика (1), сравнение которой с критическим уровнемдает наилучшее решение по правилу Неймана – Пирсона или Байеса. В радиоэлектронике гипотезапредполагает, что наблюдения(на входе один шум), гипотеза- наблюдения(на входе шум + полезный сигнал).

Гипотезы могут быть безальтернативными. Именно таковой является гипотеза о законе распределения. Действительно, пусть априори известно, что наблюдения - случайные числа(рис. 1-1). Но вокруг любой плотности распределения можно изобразить несчетное множество кривых, мало отличающихся от нее, с площадьюпод каждой (рис. 1-2).

Рис. 1. Плотности распределения

Каждая из таких плотностей соответствует закону распределения, близкому к заданному, но другому. Ясно, что множества , порожденные такими распределениями, неразличимы. Поэтому можно лишьутверждать, что наблюдениямогли быть извлечены из предполагаемого гипотезой множества. Итак, ответ на вопрос о правильности гипотезы о законе распределения (безальтернативной, односторонней) формулируется так: есть основания (или нет) отвергнуть гипотезу. Принять одностороннюю гипотезу нельзя.

Следует подчеркнуть, что формулировка “наблюдаемая величина распределена по такому – то закону” недостаточна. Гипотеза должна быть дополнена значениями параметров. Нормальное распределение описывается двумя параметрами –

м. о. и дисперсией, показательное распределение и распределение Релея – одним параметром и т. д. [2]. Чаще всего значения параметров априори неизвестны, поэтому сначала надо параметры оценить. Методы оценивания параметров распределений разрабатываются в математической статистике. Широко используются оценки максимального правдоподобия [1].

Таким образом, если параметры гипотетического закона распределения неизвестны, сначала необходимо их оценить, и только после этого можно сформулировать конкретную гипотезу. Так, гипотеза нормальности формулируется после получения, например, МП – оценок

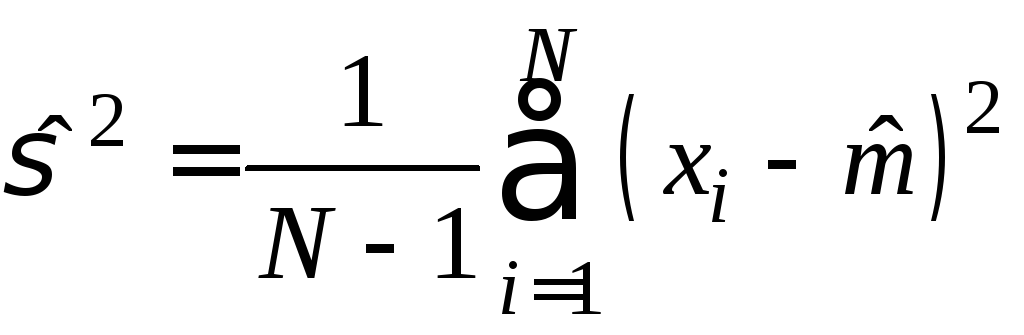, . (2)

2. Гистограмма

Обычно экспериментальные результаты сравниваются с теоретическими. Теоретическую (гипотетическую) плотность распределения нетрудно изобразить, например, в системеMATLAB, как на рис. 1-1 для ,. Экспериментальная плотность изображается в виде гистограммы [1]. Гистограмма – ступенчатая кривая, показывающая относительное количество попаданийнаблюдаемой величины в- й интервал значений. При разбиении общего промежутка значенийотдонаравных интервалов размером

сумма . В соответствии с классическим определением вероятности события как его относительной частоты [2] наилучшая оценка вероятности есть [1]

. (3)

Таким образом, гистограмма – последовательность оценок (3) вероятностей попадания наблюдений в интервалы разбиения, то есть оценка плотности распределения.

Пример 1. Функцией RANDNформируютсязначений; оценки (2) равны,. Полученные оценки позволяют сформулировать гипотезу о нормальном распределении наблюдений с параметрамии. Гипотетическая плотность показана на рис.2. Гистограмма наблюдений (рис. 2) рассчитана функциейHIST(X,Y), аргументкоторой – вектор середин интервалов разбиения. Векторзадан таким, что длина интервалов, вероятности попаданий величиныприведены в табл. 1.

N=100000

y=-4:0.1:4;

f=normpdf(y,0,1); % гипотетическая плотность

x=randn(1,N); % формирование массива

Y=-2.5:1:2.5 % центры интервалов

h=hist(x,Y)/N % гистограмма

m=mean(x) % оценка м.о.

si=std(x)^2 % оценка дисперсии

bar(Y,h)

hold on

plot(y,f)

xlim([-4 4])

Рис. 2. Нормальная плотность и гистограмма,

табл. 1

	0.0208	0.1366	0.3413	0.3413	0.1336	0.0208
	0.0229	0.1351	0.3405	0.3408	0.1384	0.0222