8.4. Непараметрические критерии согласия

В гл. 4 мы уже упоминали об обширном классе двухальтернативных задач, связанных с проверкой гипотезы о том, что совокупность наблю­даемых данных подчиняется некоторому заданному распределению ве­роятности при свободной альтернативе, то есть в предположении, что наря­ду с выполнением этой гипотезы могут встретиться какие угодно слу­чаи. Там же был рассмотрен пример такой задачи в параметрическом варианте, когда класс возможных распределений вероятности ограничен некоторым параметрическим семейством с совершенно произвольными значениями параметров. При отсутствии такого ограничения задача приобретает дополнительную специфику, связанную с очень большой степенью априорной неопределенности и необходимостью ей непарамет­рического решения. Правило решения этой задачи, по установившейся терминологии, называется критерием согласия и неоднократно рассма­тривалось в литературе по математической статистике, являясь класси­ческим примером задачи принятия решения в условиях априорной не­определенности. Покажем, как получить известные и новые непараме­трические критерии согласия на основе адаптивного байесова подхода.

Сформулируем более четко постановку задачи. Пусть имеется сово­купность независимых наблюдений и функция распреде­ления величины () есть либо, либо, причем функция распределения известна, а функция распределенияполностью неизвестна и совершенно произвольна. На основании наблюдения совокупности данныхтребует­ся решить, какая из альтернатив имеет место в действительности:

1) - выборка описывается распределением веро­ятности с функцией распределения;

2) - выборка не описывается распределением вероятности с функцией распределения, а описывается распре­делением вероятности с какой-то иной отличной от , функцией распределения .

Обозначим решения, состоящие в принятии первой и второй аль­тернативы, через исоответственно и определим функцию потерь. Обычно для правильных решений принимаются нулевые потери , а значение потерь от принятия решения(реше­ние о том, что выборка не согласуется с заданной функцией распре­деления, когда на самом деле совокупность данных описывается функцией распределения , ()) может быть при­нято равным произвольной константе, без ограничения общности. Потериот принятия решенияо том, что выборка описывается функцией распределения , когда на самом деле она не описывается ей (), естественно задать так, чтобы они были малы, если различие между функциями распределения и мало, и увеличивались по мере роста различий между этими функ­циями распределения, то есть.

Для того чтобы задача имела нетривиальное решение, функционал должен обращаться в нуль при. Это естественное тре­бование соответствует тому очевидному факту, что при потери должны обращаться в нуль, поскольку вторая альтернатива совпадает с первой. В качестве функционала, удовлетворяющего всем перечисленным требованиям, удобно взять ту или иную меру различия в функциональном пространстве функций распределения. Примерами таких мер являются

, (8.4.1)

, (8.4.2)

и т. д.

. (8.4.3)

Зададим также априорные вероятности альтернатив ,и введем произвольное рандомизированное пра­вило решения, определив для этого решающую функцию ( - вероятность принять решение , если наблюдаемая совокупность данных есть . Тогда средний риск

(8.4.4)

естественно зависит от неизвестной функции распределения и по­этому также неизвестен.

Предположим на время, что функция распределения известна и равна, то есть речь идет о задаче проверки гипотезы с простой заданной альтернативой . Тогда, применяя обычный байесов подход, получаем нерандомизированное правило решения:

или при . (8.4.5)

Неравенство (8.4.5), определяющее условия принятия решения о том, что выборочные данные согласуются с распределением вероят­ности, задаваемым функцией распределения, можно переписать в следующем виде:

, (8.4.6)

где - некоторая функция выборочных данных, опре­деляемая при известнойлевой частью неравенства (8.4.5).

При неизвестной функции распределения в соответствии с об­щими принципами адаптивного байесова подхода нужно заменить неизвестные нам статистические описания данных наблюдения оценоч­ными значениями, полученными с помощью тех же данных наблюдения. В данном случае нам неизвестны как функция потерь - величина, зависящая от неизвестной функции распределения - так и отношение правдоподобия , входящее в функцию С = С(х) и зависящее от неизвестной плотности вероятности . Состоятельной оценкой функции распределения в предположении, что имеет место вторая альтернатива, является вы­борочная функция распределения

, (8.4.7)

где

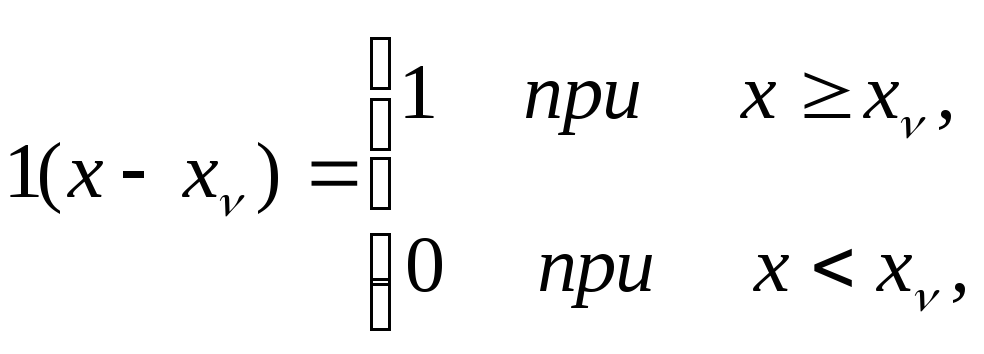(8.4.8)

а состоятельной оценкой - величина

, (8.4.9)

которая зависит от совокупности имеющихся данных . Нужно отметить, что, используя (8.4.7), мы уже израсходовали все имеющиеся данные наблюдения на оценку функции распределения и функции потерь. Такая политика в отношении распреде­ления имеющейся информации для устранения априорной неопределен­ности является в данном случае правильной, поскольку все равно без дополнительных предположений о возможном виде функции распреде­ления (то есть ограничения второй альтернативы) никакой состоя­тельной оценки плотности вероятностии функции прав­доподобия, входящей в величинуС = С(х), не существует. Лучшее, что можно сделать в этих условиях - заменить в (8.4.6) его состоятельной оценкойиз (8.4.9), а- некоторой константой.

В результате приходим к следующему правилу решения, опреде­ляющему непараметрический критерий согласия: решение о том, что совокупность данных наблюдения подчиняется рас­пределению с функцией распределения , принимается в том слу­чае, если выполняется неравенство

(8.4.10)

Различным определениям меры различия соответствуют разные критерии согласия: для (8.4.1) получается критерий Колмогоро­ва, для (8.4.2) - критерий² Мизеса - Смирнова и т. д. Константа С в (8.4.10) обычно выбирается так, чтобы вероятность принять решение , когда выполняется первая альтернатива (), была равна заданной величине.

Правило решения (8.4.10) обладает следующими свойствами асимптотической инвариантности: при распределение вероятности случайной величиныв случае, если выборкаопи­сывается функцией распределения, не зависит от вида этой функции, то есть получается универсальным для всех , а в случае, если выборка описывается функцией распределения , зависит от истинной величины. Асимптотические свойства критериев согласия (8.4.10) и их поведение при конечныхп подробно исследованы в литературе по математической статистике.

Совершенно аналогично можно получить решение некоторых более сложных задач проверки гипотезы со свободной альтернативой. Пусть, например, имеется две совокупности данных наблюдения ии требуется решить, подчиняются ли они од­ному и тому же распределению вероятности (на этот раз неизвестному) или нет. Если обозначить

, , (8.4.11)

выборочные фикции распределения, построенные по совокупности х и у соответственно, то аналогично (8.4.10) правило решения для этой зада­чи определяется следующим неравенством:

(8.4.12)

При этом меру обычно задают так, что она удовлетворяет требованиям, вытекающим из обычного определения расстояния, то есть. (Заметим, что функции из (8.4.2), (8.4.3) не отвечают этому свойству.) В частности, дляиз (8.4.1) полу­чаем известный критерий Смирнова.

Можно еще усложнить постановку задачи с учетом возникающих практических потребностей. Пусть, например, задана некоторая функ­ция , и производятся две независимые серии наблюдений и

Требуется принять решение, связаны ли эти величины заданной функциональной зависимостью, то есть являются ли случайные величины зна­чениями функцииот случайного аргумента, с тем же распределением вероятности, что и любая из величин. Осуществим преобразование случайных величин в соответствии с правилом, в результате чего получим совокупность данных. Тогда постав­ленная задача статистического решения сводится к задаче проверки ги­потезы о том, что совокупности и у подчиняются одному и тому же распределению вероятности, а непараметрическое правило ее решения дается неравенством (8.4.12), где

. (8.4.13)

В заключение отметим, что приведенные в этой главе примеры применения адаптивного байесова подхода, несмотря на довольно зна­чительную общность каждого из них, ни в коей мере не исчерпывают даже небольшой доли того громадного множества задач, которое воз­никает в практических приложениях. Однако читатель получил опреде­ленное представление о возможностях применения адаптивного байесова подхода к задачам с непараметрической априорной неопреде­ленностью и сможет применить при необходимости изложенные выше методы.