7.5.3. Переход к непрерывному времени. Дифференциальные уравнения для оценок максимального правдоподобия

Рассмотрим теперь специальный случай, когда имеющиеся данные наблюдения х описываются не совокупностью выборочных точек , а представляют собой отрезок реализации некоторого процесса , зависящего от параметров , заданный на интервале , при­чем длина этого интервала может увеличиваться при наблюдении (мо­мент времени t является переменным).

Для статистического описания данных наблюдения в этом случае вводится функционал отношения правдоподобия, представляющий собой предел при , maxотношения плотности распределе­ния вероятности совокупности значений при произ­вольно заданном значении к аналогичной плотности вероятности при некотором фиксированном значении , а в некоторых случаях, когда допускает представление , где -случай­ный процесс, не зависящий от , к плотности вероятности совокупности значений при условии, что . Использование функционала отношения правдоподобия позволяет исключить формальные труд­ности определения плотности вероятности, возникающие при переходе к непрерывному времени.

Логарифм функционала отношения правдоподобия может быть представлен в виде

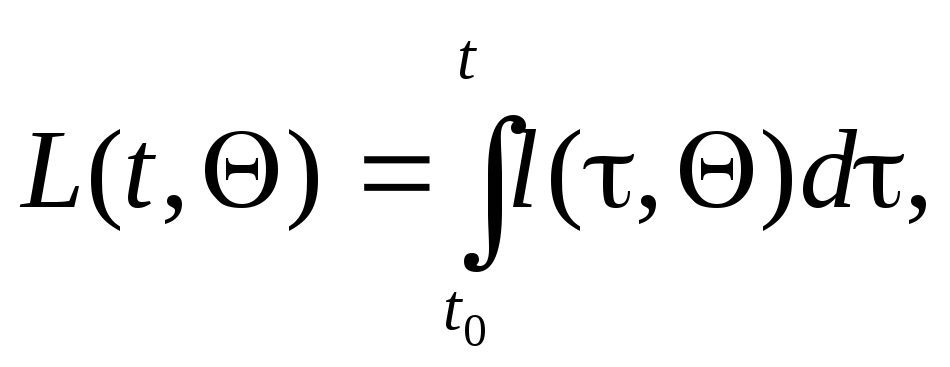(7.5.37)

где -некоторый функционал процесса на интервале . В некоторых случаях функционал вырождается в функ­цию, зависящую только от значения .Так, если

. (7.5.38)

где -известная функция времени и параметров , а - дельта-коррелированный случайный процесс («белый» шум) со спек­тральной плотностью N_o, то, выбирая в качестве знаменателя отношения правдоподобия распределения вероятности х при , будем иметь

(7.5.39)

. (7.5.40)

Пусть - оценка максимального правдоподобия параметра , построенная по реализации процесса на интервале , то есть решение уравнения максимального правдоподобия

(7.5.41)

Дифференцируя левую часть этого уравнения по времени, получаем

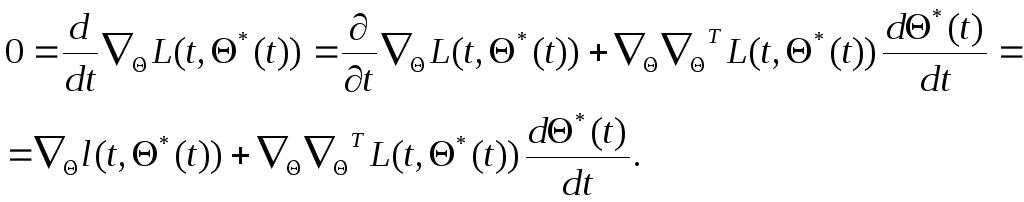(7.5.42)

Вводя обозначения

(7.5.43)

(7.5.44)

и решая уравнение (7.5.42) относительно ,получаем диффе­ренциальное уравнение для оценки максимального правдоподобия

(7.5.45)

Матрица ,в свою очередь, согласно (7.5.37) определяется диффе­ренциальным уравнением

(7.5.46)

где

(7.5.47)

Так же, как в дискретном случае, матрица в (7.5.45), (7.5.47) мо­жет быть заменена своим математическим ожиданием — информационной матрицей Фишера при значении ,а диф­ференциальное уравнение (7.5.46) для весовой матрицы - урав­нением

(7.5.48)

где аналогично дискретному случаю

(7.5.49)

- математическое ожидание матрицы вторых производных .

Совокупность дифференциальных уравнений (7.5.45), (7.5.46) или (7.5.45), (7.5.48) совместно с начальными условиями, относительно вы­бора которых остается в силе все сказанное для дискретного случая, полностью определяет оценку максимального правдоподобия для любого момента времени. Эта совокупность может быть смоделирована с помощью соответствующих, вообще говоря, нелинейных аналоговых устройств или при подходящей дискретизации по времени решена с по­мощью ЭВМ. Отметим в заключение одну из модификаций этих урав­нений, позволяющую избежать необходимости обращения матрицы .

Вводя обозначение

(7.5.50)

и дифференцируя по времени соотношение , где I - единич­ная матрица, получаем с помощью (7.5.46) дифференциальное уравне­ние, определяющее непосредственно матрицу :

и дифференцируя по времени соотношение , где I - единич­ная матрица, получаем с помощью (7.5.46) дифференциальное уравне­ние, определяющее непосредственно матрицу :

(7.5.51)

(и аналогично при замене на ), которое совместно с уравнением (7.5.45)

определяет оценку , не требуя обращения матриц. При этом имеет место переход от простейшего линейного дифференциального уравнения (7.5.46) к нелинейному относительно дифференциальному уравне­нию (7.5.51) типа Риккати.