СПб ГУАП

КАФЕДРА № 43

Рейтинг за работу __________________________________________

Преподаватель Плехоткина Г. Л.

ОТЧЕТ

о лабораторной работе по курсу

ОБЩАЯ ФИЗИКА

" Математический и Оборотный маятник "

ОФ 43.2007.1 04. лр.

Работу выполнил

студент группы № 2051 АБРАМОВ Д. А.

С-ПЕТЕРБУРГ

2000 г.

ПРОТОКОЛ

Лабораторная работа № 4

“Математический и Оборотный маятник”

студент группы № 2051 Абрамов Д. А.

Преподаватель Плехоткина Г. Л.

Задача №1

N=10 l=

t,c

Задача №2

N=10

t,c

1. Цель работы.

Цель работы: Определение ускорения свободного падения

2. Описание лабораторной установки.

Установка, используемая при измерениях: Установка состоит (см.рис.1) из математического и оборотного маятников. Математический маятник представляет собой металлический шарик 1 на бифиллярном подвесе 2. Длина подвеса может изменяться. Измеряется она с помощью линейки 3, укрепленной на стойке.

Оборотный маятник состоит из металлического стержня 4, на котором крепятся две способные перемещаться опорные призмы 5 и два груза 6, перемещения которых изменяет распределения масс. Фотодатчик 7 на нижнем кронштейне сигнализирует о прохождении маятником положения равновесия. Время измеряется миллисекундомером. Установка снабжена также счетчиком числа полных колебаний. Нажатием кнопки «Сеть» установка подключается к сети питания. Кнопка «Сброс» служит для установки нуля. После нажатия кнопки «Стоп» происходит окончания измерения числа полных колебаний и соответствующего промежутка времени.

3. Рабочие формулы.

T – период колебаний; t – время 10 колебаний; N – число коллебаний;

(2), g – ускорение свободного падения; l – длинна; =3,14

(4) - средний период.

4. Результаты измерений и вычислений.

Таблица 4.1

Результаты измерений и вычислений для задачи №1.

N=10	l=50cм	t,c	14,224	14,222	14,226	14,221	14,220	c g=9,748
		T,c	1,4224	1,4222	1,4226	1,4221	1,4220
	l=40cм	T,c	12,716	12,717	12,723	12,724	1,2728	c g=9,748
		T,c	1,2716	1,2717	1,2723	1,2724	1,2728

Таблица 4.2

Результаты измерений и вычислений для задачи №2.

N=10	l=38,5cм	t,c	12,508	12,507	12,513	12,52	1,2512	c g=9,7
		T,c	1,2508	1,2507	1,2513	1,252	1,2512

5. Пример расчетов.

Для задачи №1

6. Расчет погрешностей.

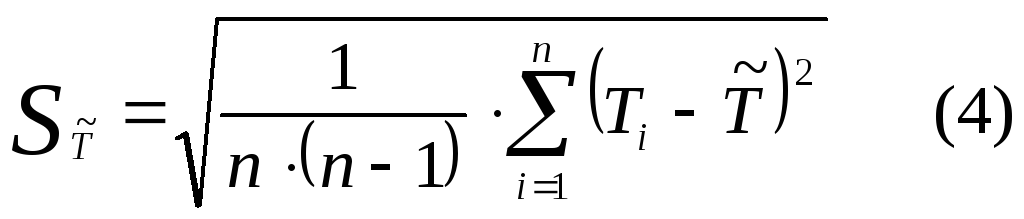
1)

2)

Для задания №1.

по формуле (4)

Для задания №2.

по формуле (4)

3)

Для задания №1.

Для задания №2.

4)

Для задания №1.

Для задания №2.

5)

Для задания №1.

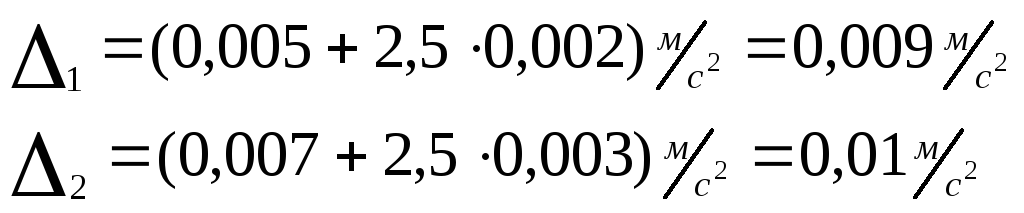n=5 то k=2,5

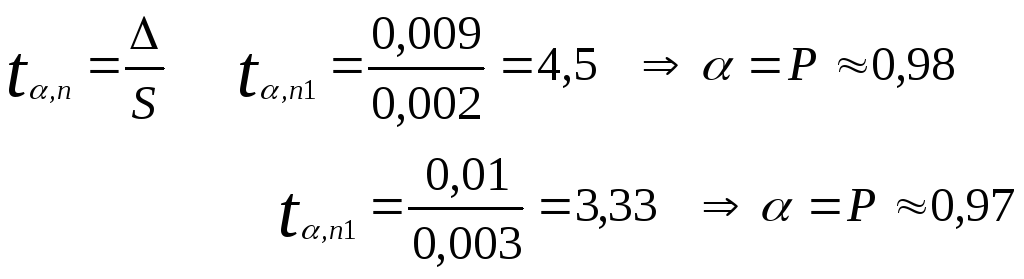
Для задания №2.

n=5 то k=2,5

7. Вывод:

При измерениях математическим маятником ускорение свободного падения равно g = (9,750,009)м/с² с вероятностью 98%.

При измерениях оборотным маятником ускорение свободного падения равно g = (9,70,009)м/с² с вероятностью 98%ю

Результаты получились почти равные. Но предпочтительнее измерять ускорение свободного падения первым способом, то есть математическим маятником, так как при измерении оборотным маятником следует искать предельную длину. При этом погрешность будет .