Эконометрика / Тема3(СЭУ)

Тема 3. Лекция 1.

СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения. Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить какая из них является зависимой, а какая независимой (фактором) переменной.

Например, традиционная модель спроса и предложения должна объяснять соотношения между ценой и объемом выпуска, характерные для некоторого определенного рынка. Поэтому она должна содержать 3 уравнения:

1. уравнение спроса (войдет доход);

2. уравнение предложения (войдет цена);

3. уравнение реакции рынка.

Делается это для того, чтобы создать более полную, адекватную модель изучаемого явления.

Более претенциозные модели содержат гораздо большее число уравнений и с их помощью пытаются отразить поведение существенно большего числа переменных.

Например, «Бруклинский проект», разработанный в США включает 359 уравнений и 56 тождеств.

Голландская эконометрическая модель: 53 уравнения и используется для прогнозирования экономической политики страны.

В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:

• Экзогенные (независимые) – значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) (X);

• Эндогенные (зависимые) - значения которых определяются внутри модели, или взаимозависимые (Y).

• Лаговые – экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например: Y_t – текущая эндогенная переменная,

Y_t-1 – лаговая эндогенная переменная,

Y_t-2 – тоже лаговая эндогенная переменная.

• Предопределенные переменные –переменные определяемые вне модели. К ним относятся лаговые и текущие экзогенные переменные (X_t, X_t-1), а также лаговые эндогенные переменные (Y_t-1).

Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (Y) рассматривается как функция одного и того же набора факторов (Х):

Набор факторов в каждом уравнении может варьировать. Так, модель вида:

y₁=f(x₁,x₂,x₃,x₄,x₅,u₁)

y₂=f(x₁,x₃,x₄,x₅,u₂)

y₃=f(x₂,x₃,x₅,u₃)

y₄=f(x₃,x₄,x₅,u₄)

также является системой независимых уравнений.

Отсутствие того или иного фактора в уравнении системы может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак (незначимо значение t–критерия или частного F–критерия для данного фактора).

2. Система рекурсивных уравнений, когда зависимая переменная одного уравнения выступает в роли фактора в другом уравнении:

В данной системе зависимая переменная включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов х. Примером такой системы может служить модель производительности труда и фондоотдачи вида:

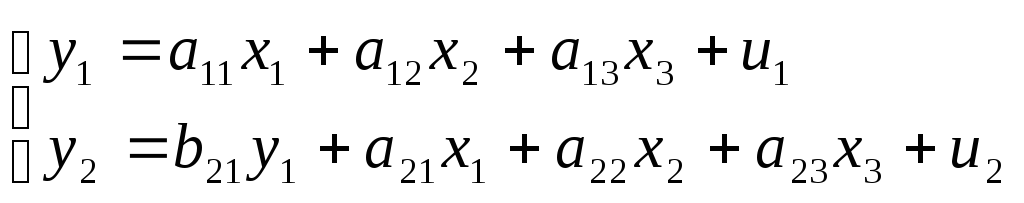
где y1 –производительность труда;

y2 – фондоотдача;

x1 – фондовооруженность труда;

x2 – энерговооруженность труда;

x3 – квалификация рабочих.

В рассмотренных 2-ух видах систем каждое уравнение может рассматриваться самостоятельно, и параметры уравнения определяются с помощью метода наименьших квадратов (МНК).

3. Система взаимозависимых (совместных, одновременных) уравнений, когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

Название система одновременных уравнений подчеркивает тот факт, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других.

В эконометрике эта система уравнений также называется структурной формой модели.

В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим, т.к. нарушаются следующие предпосылки, лежащие в основе МНК:

1. Причинно-следственная зависимость между переменными в уравнении. В первом уравнении y1 есть функция от y2, во втором уравнении y2 есть функция от y1.

2. Отсутствие взаимосвязи между факторами (отсутствие мультиколлинеарности). Как следует из уравнения 2 системы y2 зависит от x1, но эти переменные фигурируют в качестве факторных признаков в уравнении 1 (т.е. имеет место мультиколлинеарность).

3. Независимость остатков и факторных признаков. Существует зависимость между y2 и x1, и u2 и u1 соответственно.

В результате оценки получаются смещенными

В силу вышесказанного для оценки параметров системы одновременных уравнений применяются специальные методы – косвенный и двушаговый МНК.

Примером системы одновременных уравнений служит модель Кейнса:

c=a+b∙y+u

y=c+i,

c – расходы на потребление

y – доход;

i – сбережения (инвестиции);

a,b -параметры;

u - остаток.

c и y – взаимозависимые переменные;

Структурная и приведенная формы системы одновременных уравнений

В общем виде, модель одновременных уравнений, содержащая K уравнений для M эндогенных переменных, можно представить следующим образом:

y1= b12*y2+b13*y3+...+b1k*yk+c11*x1+...+c1m*xm+u1

y2=b21*y1+ +b23*y3+...+b2k*yk+c21*x1+...+c2m*xm+u2

y3=b31*y1+b32*y3+ +...+b3k*yk+c31*x1+...+c3m*xm+u3

....

yk=bk1*y1+bk2*y2+bk3*y3+... +ck1*x1+...+ckm*xm+uk

y1...yk – эндогенные переменные;

x1...xm – предопределенные переменные, одна из них принимает значение =1, чтобы отразить параметр уравнения регрессии не содержащий переменных (свободный член). (! Предопределенными переменными могут быть и лаговые эндогенные переменные, т.е. Xi=Yj_-1)

Некоторые из уравнений системы могут быть представлены в виде тождеств, т.е. параметры этих уравнений имеют значения равные 1 (например, 2-ое уравнение в модели Кейнса).

Другие уравнения системы являются поведенческими уравнениями.

Данную эконометрическую модель называют структурной формой модели, т.к. она отражает структуру экономики или ее сектора, либо поведение экономической единицы.

Коэффициенты b,c называют структурными параметрами или коэффициентами.

От структурной формы легко перейти к так называемой приведенной форме модели, в которой все эндогенные переменные выражены через предопределенные переменные:

Пример: вновь обратимся к модели Кейнса:

c=a+b∙y+u 0<b<1

y=c+i

Запишем приведенную форму этой структурной модели, т.е. все эндогенные переменные выразим через предопределенные:

c=A1+B1*i+U1

y=A2+B2*i+U2

Введем зависимость c от i. Подставим тождество дохода в функцию потребления:

c=a+b(c+i)+u;

c-bc=a+b∙i+u;

c(1-b)=a+bi+u.

Проведя алгебраические преобразоваия получим:

c=a/(1-b)+b/(1-b)*i+u/(1-b)

A1=a/(1-b); B1=b/(1-b); U1=u/(1-b).

Функцию потребления подставим в тождество дохода:

y=(a+by+u)+i.

Проведя алгебраические преобразования получим:

y=a/(1-b)+1/(1-b)*i+u/(1-b)

A2=a/(1-b); B2=1/(1-b); U2=u/(1-b).

Получим приведенную форму модели:

c=A1+B1*i+U1

y=A2+B2*i+U2

Особенность приведенной формы: т.к. правая часть каждого из уравнений модели содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такие системы относят к независимым. Тогда параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.

Зная оценки этих коэффициентов можно определить параметры структурной формы модели (косвенный МНК). Однако им можно воспользоваться не всегда.!

Проблемы идентификации

Сущность проблемы: можно ли определить параметры структурной формы модели по оценкам приведенных коэффициентов.

Если можно, то уравнение идентифицируемо; если нет, то неидентифицируемо.

Уравнение называется точно идентифицированным, если оценки структурных параметров можно однозначно (единственным способом) найти по коэффициентам приведенной модели.

Уравнение сверхидентифицировано, если для некоторых структурных параметров можно получить более одного численного значения.

Правила идентификации

Введем следующие обозначения:

M- число предопределенных переменных в модели;

m- число предопределенных переменных в данном уравнении;

K – число эндогенных переменных в модели;

k – число эндогенных переменных в данном уравнении.

Порядковые условия идентификации:

Необходимое (но недостаточное) условие идентификации можно сформулировать 2-мя способами:

1. Для того чтобы уравнение модели, содержащей К эндогенных переменных, было идентифицируемо, это уравнение не должно включать минимум (К-1) переменных модели (как эндогенных, так и предопределенных).

Если из этого уравнения исключено ровно (К-1) переменных, то оно точно идентифицированно.

Если оно не включает больше, чем (К-1) переменных, то оно сверхидентифицированно.

2. Для того чтобы уравнение модели было идентифицируемо, необходимо, чтобы число предопределенных переменных, не входящих в уравнение, было не меньше «числа эндогенных переменных, входящих в уравнение минус 1», т.е. : M-m>=k-1;

Если M-m=k-1 , уравнение точно идентифицированно.

Если M-m>k-1, уравнение сверхидентифицированно.

! Эти правила следует применять в структурной форме модели.

Рассмотрим пример: Дана структурная форма модели спроса и предложения:

Qt=a1+b11*Pt+b12*It+u1t – функция спроса

Qt=a2+b21*Pt+b22*Pt-1+u2t - функция предложения

Предопределенные переменные:

It –доход;

Pt-1 - цена в предыдущий период времени.

Эндогенные взаимозависимые переменные:

Pt – цена

Qt – количесвто товара

Случайные переменные: u1t, u2t

Параметры модели: a,b

K=2; M=2

Для 1-ого уравнения модели (функции спроса) k= 2; m=1;

M-m=2-1=1 = k-1=2-1=1, следовательно, уравнение точно идентифицированно.

Для 2-ого уравнения (функция предложения) k=2; m=1;

M-m=2-1=1 = k-1=2-1=1, следовательно, уравнение точно идентифицированно.

Достаточное условие идентификации.

Сформулированное выше правило – необходимое, но недостаточное условие идентификации, поэтому даже если оно выполнено уравнение может оказаться неидентифицированным. Введем обозначения: А – матрица коэффициентов при переменных не входящих в данное уравнение.

Достаточное условие идентификации заключается в том, что ранг матрицы А был равен (К-1). Ранг матрицы – размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю.

Ранг матрицы – максимальное число линейно независимых строк и столбцов этой матрицы.

Пример, пусть имеется система:

y1 - a1 -b12*y2-b13*y3-c11*x1 =u1

y2 – a2 -b23*y3-c21*x1-c22*x2 =u2

y3 – a3 –b31*y1 -c31*x1-c32*x2 =u3

y4 – a4 –b41*y1-b42*y2 -c43*x3=u4

В этой системе y1-y4 - эндогенные переменные;

x1-x3 - экзогенные переменные.

В соответствии с необходимым порядковым условием идентификации каждое уравнение точно идентифицированно, т.к. К=4; К-1=3; М=3; К+М=7.

k1=3; m1=1; M-m1=2 = k1-1=2, следовательно, 1-ое уравнение точно идентифицированно.

k2=2; m2=2; M-m2=1 = k2-1=1, следовательно, 2-ое уравнение точно идентифицированно.

k3=2; m3=2; M-m3=1 = k3-1=1, следовательно, 3-е уравнение точно идентифицированно.

k4=3; m4=1; M-m4=2 = k4-1=2, следовательно, 4-ое уравнение точно идентифицированно.

Рассмотрим 1-ое уравнение этой системы. Проверим для него достаточное условие идентификации:

Составим матрицу коэффициентов при переменных: y4, x2, x3 (не входящих в уравнение 1):

y4 x2 x3

0 -с22 0 - во 2-ом уравнении

А= 0 –c32 0 - в 3-ем уравнении

1 0 -c43 - в 4-ом уравнении

Проверим, что ранг матрицы =2 (т.е. определитель матрицы А равен 0). Так как ранг матрицы (2) меньше К-1=3, то 1-ое уравнение модели не идентифициррованно.

Рассмотрим 2-ое уравнение этой системы. Проверим для него достаточное условие идентификации:

Составим матрицу коэффициентов при переменных: y1, y4, x3 (не входящих в уравнение 1):

y1 y4 x3

1 0 0 - в 1-ом уравнении

А= -b31 0 0 - в 3-ем уравнении

-b41 1 -c43 - в 4-ом уравнении

Проверим, что ранг матрицы =2 (т.е. определитель матрицы равен 0). Так как ранг матрицы (2) меньше К-1=3, то 2-ое уравнение модели не идентифициррованно.

Рассмотрим 3-е уравнение этой системы. Проверим для него достаточное условие идентификации:

Составим матрицу коэффициентов при переменных: y2, y4, x3 (не входящих в уравнение 1):

y2 y4 x3

-b12 0 0 - в 1-ом уравнении

А= 1 0 0 - во 2-ом уравнении

-b42 1 -c43 - в 4-ом уравнении

Проверим, что ранг матрицы =2 (т.е. определитель матрицы равен 0). Так как ранг матрицы (2) меньше К-1=3, то 3-е уравнение модели не идентифициррованно.

Рассмотрим 4-ое уравнение этой системы. Проверим для него достаточное условие идентификации:

Составим матрицу коэффициентов при переменных: y3, x1, x2 (не входящих в уравнение 1):

y3 x1 x2

-b13 -c11 0 - в 1-ом уравнении

А= -b23 –c21 –c22 - во 2-ом уравнении

1 -c31 -c32 - в 3-м уравнении

Проверим, что ранг матрицы =3 (т.е. определитель матрицы не равен 0). Так как ранг матрицы (3) равен К-1=3, то 4-е уравнение модели точно идентифициррованно.

Проверим модель спроса и предложения, рассмотренную ранее на достаточное условие идентификации.

Для 1-ого уравнения: Pt-1 – переменная модели, отсутствующая в данном уравнении. Ранг матрицы А в данном случае равен 1, что совпадает с К-1=1. Следовательно, уравнение 1 точно идентифицированно.

Для 2-ого уравнения: It – переменная модели, отсутствующая в данном уравнении. Ранг матрицы А в данном случае также равен 1, что совпадает с К-1=1. Следовательно, уравнение 2 также точно идентифицированно.

Сформулируем необходимое и достаточное условия идентификации:

1) Если M-m>k-1 и ранг матрицы А равен К-1, то уравнение сверхидентифицированно.

2) Если M-m=k-1 и ранг матрицы А равен К-1, то уравнение точно идентифицированно.

3) Если M-m>=k-1 и ранг матрицы А меньше К-1, то уравнение неидентифицированно.

4. Если M-m<k-1, то уравнение неидентифицированно. В этом случае ранг матрицы А будет меньше К-1.

Если уравнение неидентифицированно, то оценки его структурных параметров найти нельзя.

Модель считается точно идентифицированной, если все ее уравнения точно идентифицированны.

Если среди уравений модели есть хотя бы одно сверхидентифицированное уравнение, то вся модель считается сверхидентифицированной.

Если среди всех уравнений модели есть хотя бы одно неидентифицированное, то вся модель считается неидентифицированной.

Оценка точно идентифицированного уравнения (косвенный метод наименьших квадратов -КМНК).

Сущность КМНК состоит в получении оценок структурных коэффициентов через приведенные коэффициенты.

Условие применения этого метода – однозначное определение структурных коэффициентов через приведенные коэффициенты.

Алгоритм КМНК включает 3 шага:

1. составляется приведенная форма модели и определяется выражение каждого коэффициента приведенной формы через структурные параметры;

2. к каждому уравнению приведенной формы применяют обычный МНК, получают численные оценки приведенных параметров;

3. по оценкам приведенных коэффициентов находят оценки структурных параметров, используя соотношения, найденные на шаге 1.

Примечание: при небольшом числе переменных можно не определять приведенные коэффициенты через структурные параметры, что приводит к необходимости решения нелинейной системы уравнений, а воспользоваться более простым приемом – получить из имеющихся приведенных уравнений структурные уравнения.

Пример, пусть дана структурная форма модели спроса и предложения:

Qt=a1+b11*Pt+b12*It+u1t – функция спроса

Qt=a2+b21*Pt+b22*Pt-1+u2t - функция предложения

Предопределенные переменные:

It -доход;

Эндогенные взаимозависимые переменные:

Pt – цена

Qt – количество товара

К=2; М=2.

Имеются данные за 6 периодов времени по переменным:

t	Qt	Pt	It	Pt-1
1	95	11	12	12
2	113	10	13	11
3	92	12	13	10
4	107	13	14	12
5	114	12	15	13
6	111	13	15	12
Итого	632	71	82	70

Ранее было показано, что данная модель точно идентифицированна.

Для оценки параметров a1, a2, b11, b12, b21, b22 можно применить КМНК.

1 шаг: Составим приведенную форму:

Qt=A1+A2*It+A3*Pt-1+U1

Pt=B1+B2*It+B3*Pt-1+U2

2 шаг: Определим МНК-оценки приведенных коэффициентов по каждому приведенному уравнению в отдельности. В соответствии с методикой МНК система нормальных уравнений для расчета параметров 1-ого приведенного уравнения (А1, А2, А3) примет вид:

Qt=n*A1+A2*It+A3*Pt-1

Qt*It=A1*It+A2*It²+A3*It*Pt-1

Qt*Pt-1=A1*Pt-1+A2*Pt*It+A3*P²t-1

По данным таблицы имеем:

632= 6А1+12А2+70А3

8678=12А1+1128А2+960А3

7401=70А1+960А2+822А3

Решив систему находим, что А1=16,43; А2=4,45; А3=2,4.

Аналогично определяем параметры 2-ого приведенного уравнения (В1, В2, В3).

Окончательно приведенная форма модели имеет вид:

Qt=16,43+4,45*It+2,41*Pt-1+U1

Pt=3,8+0,69*It-0,12*Pt-1+U2

3 шаг: По имеющейся приведенной форме получим уравнение зависимости Q от P и I. Для этого выразим из 2-го уравнения Pt-1, для простоты не будем учитывать ошибки U1, U2.

Pt-1= -8,4Pt+31,8+5,8It

Подставив найденное выражение в 1-ое уравнение приведенной формы:

Qt=16,43+4,45*It+2,41*(-8,4Pt+31,8+5,8It)=93+18,43It-20,24Pt.

Следовательно, a1=93; b11=-20,24; b12=18,43.

Аналогично можно определить параметры 2-ого структурного уравнения. Для этого нужно выразить переменную It из 2-го уравнения приведенной формы и подставить это выражение в 1-ое приведенное уравнение вместо It. Тогда получим:

a2=-8,08 ; b21=6,45 ; b22=3,18.

Структурная форма модели имеет вид:

Qt=93+18,43It-20,24Pt+u1.

Qt=-8,08+6,45Pt+3,18Pt-1+u2.

Коэффициенты детерминации R²₁=0,546; R²₂=0,550.

Для сравнения обычный МНКдает следующие результаты:

Qt=48,7+9,423It-6,09Pt+u1.

Qt=53-1Pt+5,5Pt-1+u2.

Это смещенные оценки структурных параметров модели.

Оценка сверхидентифицированног уравнения (двухшаговый метод).

Вернемся к модели спроса и предложения и введем новую предопределенную переменную Rt – благосостояние потребителей в 1-ое уравнение этой модели.

Qt=a1+b11*Pt+b12*It+b13*Rt+u1t – функция спроса

Qt=a2+b21*Pt+b22*Pt-1+u2t - функция предложения

Самостоятельно показать, что функция спроса точно идетифицированна, а функция предложения сверх идентифицированна и что выполняется достаточное условие идентификации.

Параметры сверх идентифицированной функции предложения нельзя определить косвенным МНК. Обычный МНК также нельзя применять, т.к. в этом случае были бы нарушены предпосылки применения этого метода. Нарушение этих предпосылок связанно с наличием в уравнении в качестве фактора эндогенной перменной Pt.

Предположим, что мы нашли переменную Pt’, которой можно заменить переменную Pt и для которой выполняются предпосылки МНК, т.е. переменная Pt’ должна иметь 2 свойства:

1. она должна тесно коррелировать с переменной Pt;

2. она не должна коррелировать с ошибкой U2.

Такие преобразованные переменные в эконометрике называются инструментальными переменными.

Если можно найти такую переменную и заменить ею Pt, то к уравнению Qt=a2+b21*P’t+b22*Rt+u2’

можно применить обычный МНК.

Алгоритм этого метода:

1 шаг: выпишем приведенную форму модели:

Qt=A1+A2*It+A3*Pt-1+A4*Rt+U1

Pt=B1+B2*It+B3*Pt-1+B4*Rt+U2

Из второго уравнения модели можно найти расчетные значения Pt’: Pt’=B1+B2*It+B3*Pt-1+B4*Rt.

Второе уравнение приведенной формы можно переписать в виде:

Pt=Pt’+U2

Таким образом, переменная Pt состоит из 2-ух элементов:

1. Pt’, которая есть линейная комбинация преопределенных переменных;

2. и U2, которая в соответствии с предпосылкой МНК не коррелирует с переменной Pt’.

2 шаг: сверхидентифицированную функцию предложения можно переписать в виде:

Qt=a2+b21*(Pt’+U2)+b22*Pt-1+u2 или Qt=a2+b21*Pt’+b22*Pt-1+u2’

Где u2’=u2+b21*U2.

Полученное уравнение отличается от исходной функции предложения только тем, что переменная Pt заменена на ее оценку Pt’ и ошибкой u2’. Pt’ имеет следующие свойства:

1) Она тесно коррелирует с Pt;

2) Она не коррелирует с ошибкой u1 и будучи линеной комбинацией предопределенной переменной не коррелирует с u2.

К полученному уравнению можно применять обычный МНК.

Таким образом, процедура применения двухшагового МНК предполагает:

1. определение приведенных коэффициентов модели обычным МНК и определение расчетных значений эндогенных переменных, которые фигурируют в качестве факторов в структурной форме модели;

2. определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в качестве факторов входящие в это уравнение предопределенные переменные и оценки эндогенных переменных, полученные на шаге 1.

Пример, добавим в таблицу исходных данных значения Rt (благосостояния).

T	Qt	Pt	It	Pt-1	Rt	Pt’
1	95	11	12	12	25	11,04
2	113	10	13	11	24	10,54
3	92	12	13	10	25	11,57
4	107	13	14	12	27	12,68
5	114	12	15	13	26	11,68
6	111	13	15	12	28	13,5
Итого	632	71	82	70	155	71

Определим обычным МНK параметры приведенной формы модели, используя данные таблицы:

Qt=62,41+7,52It+3,02Pt-1 -3,68Rt+U1 R²=0,685

Pt=-6,036+0,036*It-0,25*Pt-1+0,786*Rt+U2 R²=0,864

Подставим во 2-ое уравнение приведенной формы значения It, Pt-1, Rt из таблицы и найдем расчетные значения Pt’ и добавим их в таблицу.