Нелинейная Регрессия

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы: ; параболы второй степени:(i=1;n) и др.

Различают два класса нелинейных регрессий:

• Регрессии, нелинейные относительно включенных в анализ объясняющих переменных (факторов), но линейные по оцениваемым параметрам;

• Регрессии, нелинейные по оцениваемым параметрам.

Нелинейные регрессии по объясняющим переменным (факторам), но линейные по оцениваемым параметрам.

Данный класс нелинейных регрессий включает уравнения, в которых результирующая переменная - y линейно связана с параметрами, но нелинейно связана с объясняющими переменными. Примером могут служить следующие функции:

• Полиномы разных степеней – (полиномk-ой степени);

• Равносторонняя гипербола – .

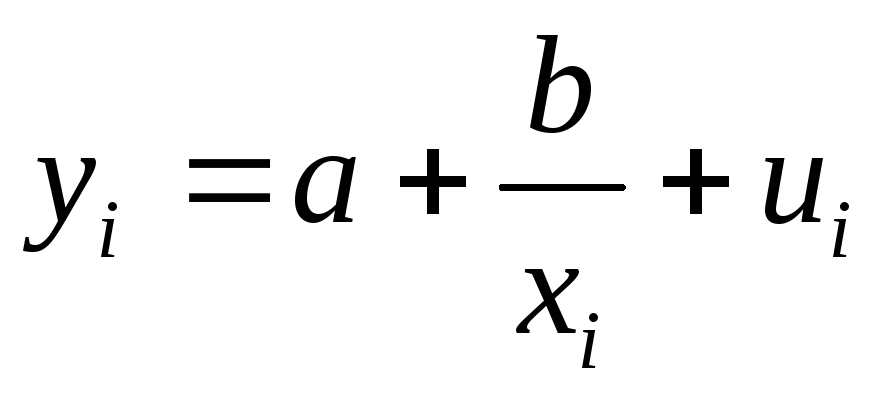Оценка параметров регрессий нелинейных по объясняющим переменным.

При этом используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

Рассмотрим применение данного подхода к параболе второй степени:. Заменяя переменную х²наzполучим двухфакторное уравнение линейной регрессии:, для оценки параметров которого используется обычный МНК.

Соответственно, для полинома k-ого порядка:, при замене:z₁=x,z₂=x²,z₃=x³, ...,z_k=х^k, получим:.

Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.

Парабола второй степени (см. рис.3) целесообразна к применению, если для определенного интервала значений фактора меняется характер связи с результатом: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака:

x^o=-b/2c; y^o=a-b²/4c .

y y

c>0 c<0

y^o

y^o

x

x^o x^o

Рис.3. Параболическая зависимость.

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второй степени становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

Рассмотрим как оценивают параметры в случае равносторонней гиперболы:. Для этого заменим 1/х наz, получим линейное уравнение регрессии:, параметры которого оценивают обычным МНК.

Равносторонняя регрессия может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции.

При b>0 имеем обратную зависимость, которая при ххарактеризуется нижней асимптотой, т.е. минимальным предельным значениемy, оценкой которого служит параметр а (см. рис.4.а). Приb<0 имеем медленно повышающуюся функцию с верхней асимптотой приx, т.е. максимальным предельным уровнемy, оценкой которого служит параметр а (см. рис.4.б).

a

b>0b<0

a

а) б)

Рис. 4. Зависимость в виде равносторонней гиперболы.

Регрессии нелинейные по оцениваемым параметрам.

К данному классу регрессий относятся уравнения, в которых результирующая переменная - y нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:

• Степенная – ;

• О

  Y

  братная -;

• Показательная- ;

• Экспоненциальная - ;

• Логистическая кривая (кривая Перла-Рида) -

• Кривая Гомперца -

Последние два вида кривых используются в случае, когда х=t(переменная времени).

Данный класс нелинейных моделей подразделяется на два типа:

1. нелинейные модели внутренне линейные;

2. нелинейные модели внутренне нелинейные.

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если женелинейная модель внутренне нелинейная, то она не может быть сведена к линейной функции.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении зависимости спроса от цен:, гдеy– спрашиваемое количество;x– цена;u- случайная ошибка.

Данная модель нелинейна относительно оцениваемых параметров, т.к. включает параметры aиbнеаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основаниюeприводит его к линейному виду:lny_i=lna+b·lnx_i+lnu_i. Заменив переменные и параметры (y*_i=lny_i;x*_i=lnx_i;u*_i=lnu_i;A=lna), получим линейную регрессию:

y*_i=A+b·x*_i+u*_i.

Оценки параметров А и bмогут быть найдены обычным МНК.

Обратная функция:y_i= 1/(a+b·x_i+u_i), являющаяся разновидностью гиперболы, может быть линеаризирована путем следующего преобразования - возведения в минус первую степень левой и правой частей уравнения и замены переменной 1/y=z. Тогда модель принимает вид:z_i=a+b·x_i+u_i .

Экспоненциальную модель y=e^a+bXuможно свести к линейной, логарифмируя ее по натуральному основанию. В результате получим линейную форму модели:lny=a+bX+lnu.

Преобразование логистической кривойк линейному виду (возможно, если параметра известен):,

,,.

Произведя замену переменных и параметров (y*_i=ln[(a-y_i)/y_i];B=lnb; С=-с) получим линейную регрессию:y*_i=B+Cx_i+u_i.

Преобразование кривой Гомперцак линейному виду невозможно:. То есть данная модель относится к виду нелинейных регрессий по параметрам внутренне нелинейным.

В рассматриваемой выше степенной функции предполагалось, что случайная составляющая uмультипликативно связана с объясняющей переменнойx. Если же модель представить в виде, то она становится внутренне нелинейной, т.к. ее невозможно преобразовать к линейному виду.

Если модель внутренне нелинейная по параметрам, то для оценки параметров используются итеративные процедуры (например, нелинейный МНК), успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Нелинейный МНК.

Согласно критерию МНК: строят систему уравнений, которая в случае нелинейной функцииy’ будет системой нелинейных уравнений. Решить такую систему традиционными способами (методами Гаусса, Крамера) невозможно. Нужно использовать итеративные процедуры. Например, метод Ньютона-Рафсона.

Введем обозначения:

.

Согласно методу Ньютона-Рафсона нужно найти производные f1,f2,f3 поk,a,b. Задаться начальными значениямиk0,f0,b0 (например,k0=1,a0=1,b0=0) и найти приращения (k,a,b) решив систему:

Найденные приращения прибавляем к начальным значениям параметров и получаем новые значения: k1=k0+k,a1=a0+a,b1=b0+b.

Затем составляется новая система, в которой производные f1,f2,f3 рассчитываются для новых значений параметров (k1,a1,b1). Решив эту новую систему находят новые значения приращений (k,a,b), на основе которых вычисляют следующие значения параметров:k2=k1+k,a2=a1+a,b2=b1+bи т.д.

Процесс повторяют до тех пор, пока очередные приращения (k,a,b) не будут превышать заданную степень точности (т.е. будут0).

Применение МНК для оценки параметров нелинейных по параметрам регрессий внутренне линейных.

В моделях нелинейных по оцениваемым параметрам, но приводимым к линейному виду, МНК применяется к преобразованным уравнениям. В таких моделях преобразованию подвергается результативная переменная - y, в отличие от нелинейных моделей 1-ого типа, где результативная переменная остается неизменной, а преобразуются объясняющие переменные.

Если в линейной модели и моделях, нелинейных по объясняющим переменным, при оценке параметров исходят из критерия (y-y’)²min, то в моделях, нелинейных по параметрам, требование МНК применяется не к исходным данной результирующей переменной, а к ее преобразованной величине, т.е. кlny, 1/y. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений логарифмов:

(lny- )²min или (-) ²min .

Соответственно, если в линейных моделях и моделях нелинейных по объясняющим переменным (y-y’)=0, то в моделях нелинейных по параметрам:

(lny-’)=(lny - y*’)=0 или (1/y-(1/y)’)= (1/y - y*’)=0.

Однако:

.

Вследствие этого оценка параметров с помощью МНК для нелинейных моделей внутренне линейных оказывается несколько смещенной.Поэтому при оценивании параметров таких моделей особое внимание следует уделять выполнению предпосылок нормальной классической модели множественной регрессии.

Рассмотрим оценивание параметров степенной зависимости: применяется МНК к линеаризованному уравнениюlny=lna +b·lnx+lnu, т.е. решается система нормальных уравнений:

lny=n·lna+blnx

lny·lnx=lna·lnx+b(lnx)²

Параметр b определяется непосредственно из системы, а параметр а - косвенным путем после потенциирования величины lna.

Поскольку параметр аэкономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной, т.е. как: lny=А+b·lnx(А=lna).

В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно в функциях спроса параметр b<0, а в функциях предложения: b>0.