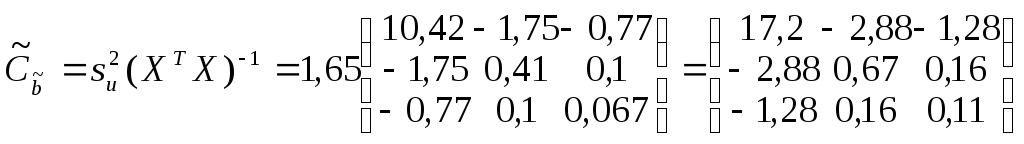Ковариационная матрица мнк-оценок параметров регрессии.
Это матрица ковариаций оценок параметров
,
размером (m+1)(m+1).
Для случая парной регрессии это матрица
размером 2×2:
.
В случае множественной регрессии (m>1) данная матрица рассчитывается следующим образом:
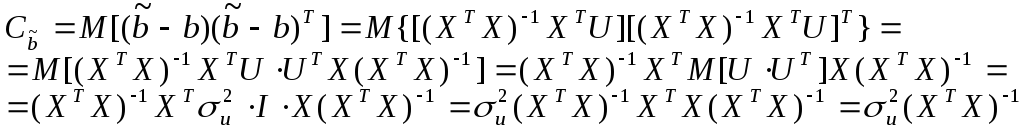
При выводе использовалось следующие преобразования:
.
!
.
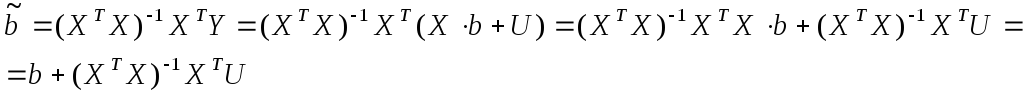
На главной диагонали данной матрицы находятся дисперсии МНК-оценок параметров. Для случая парной линейной регрессии формулы расчета дисперсий МНК-оценок параметров следующие:
,
,
где 2u – дисперсия случайной составляющей;
2x – дисперсия факторного признака х.
Так как 2u
нам неизвестна, то при расчете
ковариационной матрицы пользуются
оценкой дисперсии случайных составляющих
- s2u.
Тогда получим оцененную ковариационную
матрицу:
=
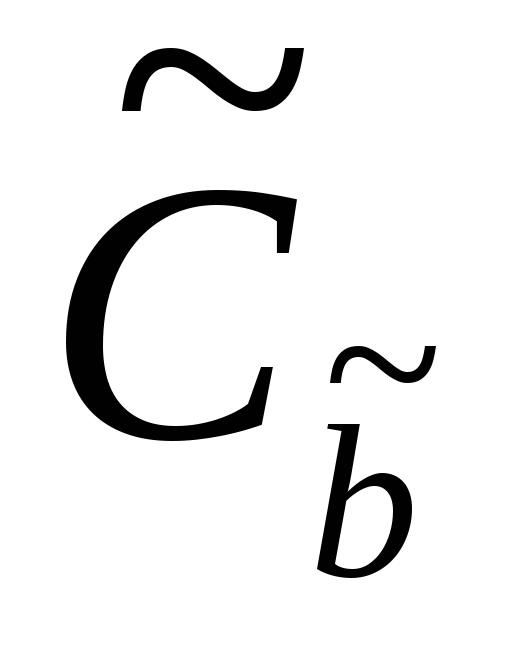s2(XT·X)-1.
Формулы расчета оценок дисперсий МНК-оценок параметров (полученные через s2u) в случае парной линейной регрессии будут следующими:
,
.
Корень из оценки дисперсии
и
называют стандартными ошибками
и
.
Найдем оценку ковариационной матрицы для нашего примера:
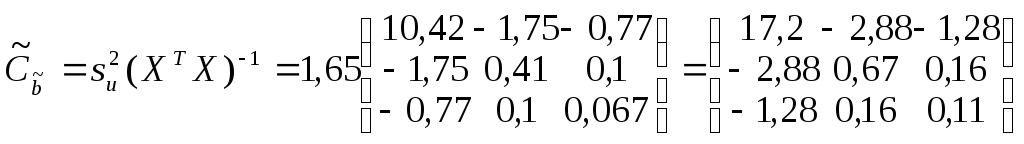
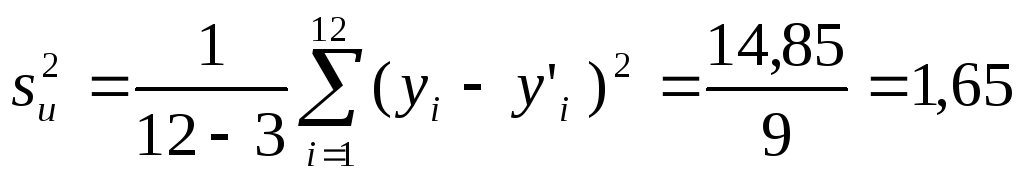
=17,2;
=0,67;
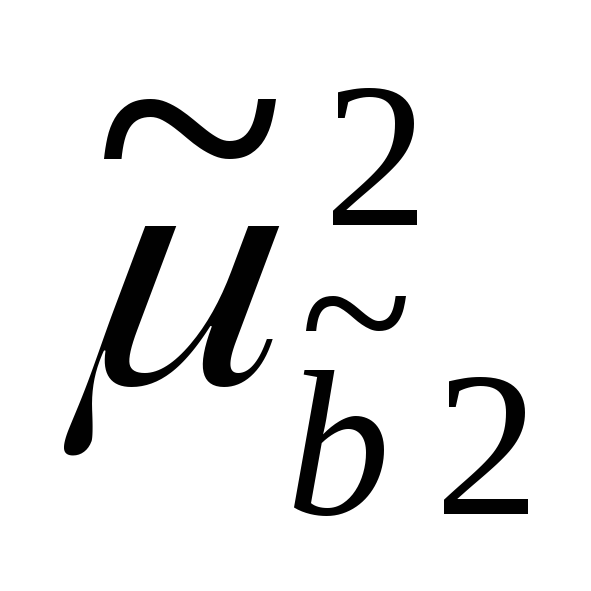=0,11.
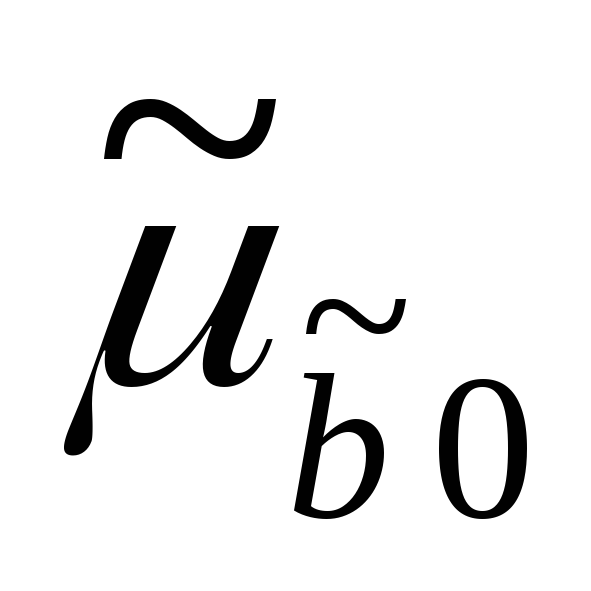=4,15;
=0,82;
=0,33.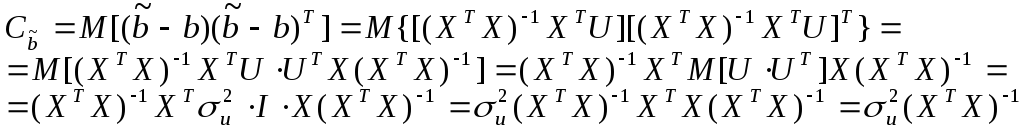