Множественный регрессионный анализ (эконометрическая модель в виде одного регрессионного уравнения)

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. В экономике (в отличие от естественных наук) невозможно контролировать поведение большинства экономических факторов. Однако влияние данных факторов можно учитывать в модели. То есть можно построить модель (уравнение), описывающую множественную связь:

y=f(x₁, x₂, ...,x_m, u) (*),

где y – признак-результат;

x₁, x₂, ...,x_m - признаки-факторы;

u – случайная составляющая.

Причины существования случайной составляющей u_i:

1) Отсутствие в модели «важных» факторов, оказывающих существенное влияние на результат. Парная регрессия почти всегда является большим упрощением. В действительности существуют другие факторы, которые не учтены в модели (*). Это могут быть факторы, которые мы не можем измерить (например, психологические факторы). Возможно это факторы, которые мы можем измерить, но которые оказывают очень слабое влияние на результат, и поэтому мы их не учитываем в модели. Кроме того, это могут быть «важные» факторы, которые мы такими не считаем из-за отсутствия опыта. Все это приводит к тому, что наблюдаемые значения лежат вне линии регрессии.

2) Агрегирование переменных. Мы можем пытаться построить зависимость путем агрегирования (объединения) индивидуальных соотношений. Например, функцию суммарного потребления, как агрегирование функций потребления по отдельным потребителям. Так как параметры индивидуальных соотношений различны, то агрегированная зависимость будет приближенной и будут расхождения между фактическим и теоретическим значениями результата - y.

3) Неправильная функциональная спецификация модели (вид функции -f).

4) Ошибки измерения переменных.

Задачи анализа многофакторной зависимости:

1. сравнение степени влияния различных факторов на результат;

2. выделение прямого (непосредственного) влияния фактора на результат и косвенного (опосредованного) влияния фактора на результат (через другие факторы);

3. выявление существенности влияния данного фактора (или группы факторов) на результат на фоне других факторов (т.е. нельзя ли исключить из модели данный фактор без существенного ухудшения описания результирующей переменной).

Изобразим графически связи всех признаков для двухфакторной регрессии: y=f(x₁,x₂,u) (рис.1).

Рис. 1. Граф связей модели: y=f(х₁, х₂).

Нормальная линейная модель множественной регрессии.

Естественным обобщением линейной парной регрессии является многомерная регрессионная модель (multiple regression model) или модель множественной регрессии:

y_i=b₀+b₁·x_i1+b₂·x_i2+...+b_j·x_ij+…+b_m·x_im+u_i , i=1;n.

где y_i- значение признака-результата (зависимой переменной) для i–ого наблюдения;

x_ji- значение j–ого фактора (независимой или объясняющей переменной) (j=1;m) для i–ого наблюдения;

u_i – случайная составляющая результативного признака для i–ого наблюдения;

b₀ – свободный член, который формально показывает среднее значение y при х₁=х₂=…=х_m=0 (или среднее значение результата, сформировавшееся под влиянием неучтенных в модели факторов).

b_j- коэффициент «чистой» регрессии при j–ом факторе (j=1;m). Он характеризует среднее изменение признака-результата y с изменением соответствующего фактора х_j на единицу, при условии, что прочие факторы модели не изменяются и фиксированы на средних уровнях.

Обычно для многомерной регрессионной модели делаются следующие предпосылки (условия Гаусса-Маркова):

1. (x_1i, x_2i,…, x_ji,…, x_mi) – детерминированные (нестохастические) переменные;

2. М(u_i)=0 , i=1;n – математическое ожидание случайной составляющей равно 0 в любом наблюдении;

3. М(u_i²)=²_ui= ²= const , i=1;n – теоретическая дисперсия случайной составляющей постоянна для всех наблюдений.

4. М(u_i, u_j)=Cov(u_i, u_j)=0 (ij) – отсутствие систематической связи между значениями случайной составляющей в любых 2-ух наблюдениях.

5. Часто добавляется условие: u_i N(0, ²), т.е. u_i – нормально распределенная случайная величина.

Первая предпосылка - сильное предположение. Иногда достаточно сделать предположение о независимости распределения случайной составляющей u_i от х_i.

Третья предпосылка - о независимости дисперсий случайной составляющей от наблюдения называется гомоскедастичностью (homoscedasticity в переводе означает одинаковый разброс). Случай, когда условие гомоскедастичности не выполняется называется гетероскедастичностью (heteroscedasticity - неодинаковый разброс).

Четвертая предпосылка указывает на некоррелированность случайных составляющих для разных наблюдений. Это условие нарушается в случае, когда данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции случайных составляющих (serial correlation).

Модель линейной множественной регрессии, для которой выполняются данные предпосылки, называется нормальной линейной регрессионной (classical normal regression model).

В матричной форме нормальная (классическая) регрессионная модель имеет вид:

Y=X·b + u

Где Y- вектор-столбец размерности (n1) наблюдаемых значений результативного признака.

X – матрица размерности (n(m+1)) наблюдаемых значений факторных признаков. Добавление 1 к общему числу факторов (m) учитывает свободный член (b₀) в уравнении регрессии. Значения фактора (х₀) для свободного члена принято считать равным единице.

b – вектор-столбец размерности ((m+1)1) неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии).

u - случайный вектор-столбец размерности (n1) ошибок наблюдений.

Предпосылки для модели в матричной форме:

1) (x₁, x₂,…, x_j,…, x_m) – детерминированные (нестохастические) переменные, т.е. ранг матрицы Х равен m+1<n;

2) М(u)=0ⁿ ;

3,4) ковариационная матрица должна иметь вид:

С_u===σ²_u·I, где σ²_u – дисперсия случайной составляющей; I – единичная матрица размером n×n.

5) u N(0, ²_u),

Традиционный метод наименьших квадратов для многомерной регрессии (OLS – Least Squares).

Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии (b₀,b₁,…,b_m) - вектора b размерности (т + 1).

Пусть имеется п наблюдений вектора х и зависимой переменной у. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть п  т+1. Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собой х и у для имеющихся наблюдений абсолютно точно. Если, в частном случае, п = т+1, то оценки коэффициентов b рассчитываются един­ственным образом. Например, при двух объясняющих переменных в уравнении = ₀+₁х₁ +₂х₂ и трех наблюдениях для оценки параметров нужно решить систему:

y₁=₀+₁х₁₁ +₂х₂₁

y₂=₀+₁х₁₂ +₂х₂₂

y₃=₀+₁х₁₃ +₂х₂₃

Система из двух уравнений содержит три неизвестных (₀, ₁, ₂). Следовательно, можно найти одно единственное значение вектора коэффициентов.

Если число наблюдений больше минимально необходимого, то есть п > т+1, то уже нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, то есть выбора наилучшей формулы-приближения для имеющихся наблюдений. Положительная разность (п-т-1) в этом случае называется числом степеней свободы. Если число степеней свободы мало, то статистическая надежность оцениваемой формулы невысока. Так, если проведена плоскость "в точности" через имеющиеся три точки наблюдений, любая четвертая точка-наблюдение из той же генеральной совокупности будет практически наверняка лежать вне этой плоскости, возможно - достаточно далеко от нее. Обычно при оценке множественной регрессии для обеспечения ста­тистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.

Оценка параметров многомерной модели, как и в случае парной регрессии, осуществляется обычно традиционным методом наименьших квадратов (МНК). Согласно данному методу в качестве оптимальной («наилучшей») оценки вектора b принимают вектор , который минимизирует сумму квадратов отклонений наблюдаемых значений y_i от рассчитанных по модели : .

В матричной форме функционал S будет записан так:

МНК-оценки в матричной форме находят по формулам:

, где .

Рассмотрим применение МНК путем решения системы алгебраических уравнений при оценивании параметров линейной двухфакторной модели:

y_i=b₀+b₁·x_1i+b₂·x_2i +u_i , i=1;n..

Для этого минимизируем функционал:

.

Функционал S является функцией 3-ех переменных , , . Чтобы найти экстремум функции нескольких переменных нужно взять ее частные производные по этим переменным и приравнять их нулю:

=0, =0, =0.

Получим следующую систему нормальных линейных уравнений:

Формула расчета оценки параметра из данной системы:

.

Аналогично рассчитывается оценка .

В общем случае, система линейных уравнений может быть решена методами: К.Гаусса, Крамера (определителей), методом итераций.

* Пример. Имеются данные об объеме продаж магазина– y (тыс.ден.ед. за период), численности населения в торговой зоне –х₁ (тыс.чел.), расстоянии от магазина до центра –х₂ (км) по 12 магазинам розничной торговли, принадлежащем одному владельцу (см. таблицу). Требуется построить регрессионную модель, для прогноза объема продаж.

Возьмем регрессионную модель в виде линейного двухфакторного уравнения регрессии: y_i=b₀+b₁·x_1i+b₂·x_2i +u_i .

Оценим параметры этого уравнения с помощью МНК.

Расчет необходимых сумм для системы нормальных линейных уравнений сведем в таблицу.

Таблица.

i	y-объем продаж, тыс.ден.ед. за период	х1- численность населения в торговой зоне, тыс.чел.	х2- расстояние от магазина до центра, км	yх1	yх2	х12	х22	х1x2
1	2	3	4	5	6	7	8	9
1	27	1,6	9,7	43,2	261,9	2,56	94,09	15,52
2	26	1,7	10,7	44,2	278,2	2,89	114,49	18,19
3	28	1,9	9,5	53,2	266	3,61	90,25	18,05
4	31	1,9	8	58,9	248	3,61	64	15,2
5	30	2	9,3	60	279	4	86,49	18,6
6	31	2	6,1	62	189,1	4	37,21	12,2
7	32	2,1	7,5	67,2	240	4,41	56,25	15,75
8	35	2,5	7	87,5	245	6,25	49	17,5
9	33	2,8	8,8	92,4	290,4	7,84	77,44	24,64
10	33	3	7,1	99	234,3	9	50,41	21,3
11	36	3,1	6,5	111,6	234	9,61	42,25	20,15
12	38	3,3	7,2	125,4	273,6	10,89	51,84	23,76
Сумма	380	27,9	97,4	904,6	3039,5	68,67	813,72	220,86
Ср.	31,67	2,325	8,12	75,38	253,29	5,72	67,81	18,41
СКО	3,47	0,53	1,39

Тогда система нормальных линейных уравнений будет иметь вид:

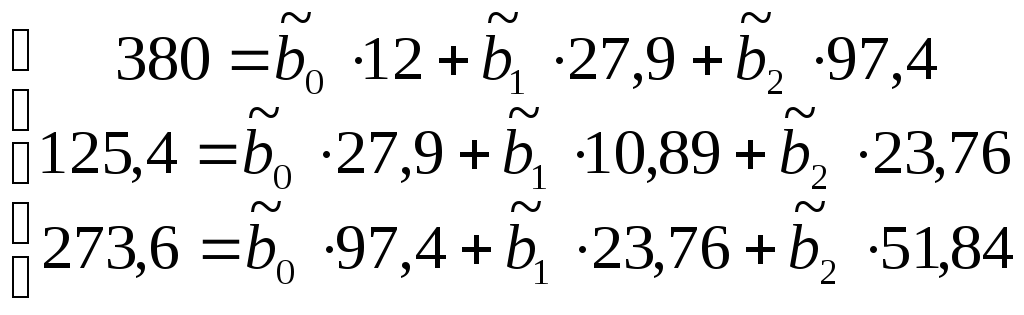
Решив систему, найдем значения , , :

= 29,4; = 4,2 ; = -0,92.

Найдем МНК-оценки для нашего примера матричным способом.

Воспользовавшись правилами умножения матриц будем иметь:

X^TX==

=.

X^TY==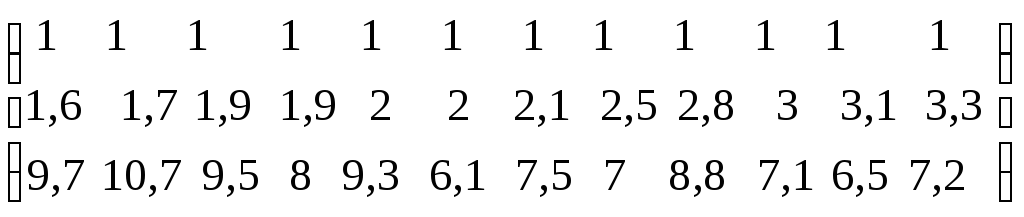

=.

Найдем обратную матрицу.

Матрицей обратной к матрице А, называется матрица А^-1, такая, что АА^-1=I (I-единичную матрицу).

Обозначим a_ij элементы матрицы А^-1. Тогда , где М_ji –матрица, получающаяся из А вычеркиванием j-й строки и i-ого столбца.

Для нашего примера: |A|==680,99;

|M₁₁|==7099,013;

a₁₁=(-1)²·7099,013/680,99=10,42 и т.д.

В результате получим:

(Х^ТХ)^-1=^-1=.

Тогда вектор оценок коэффициентов регрессии равен:

=·=.

То есть = 29,4 ; = 4,2 ; = -0,92 (оценки такие же, что и найденные 1-ым способом).

Кроме того, для линейной множественной регрессии существует другой подход получения МНК-оценок параметров - через -коэффициенты (параметры уравнения регрессии в стандартных масштабах).

При построении уравнения регрессии в стандартном масштабе все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:

, j=1;m,

где х_ji - значение переменной x_j в i-ом наблюдении.

_.

Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение (). Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:

. (β₀=0).

-коэффциенты могут быть оценены с помощью обычного МНК.

При этом система нормальных уравнений будет иметь вид:

r_x1y=₁+r_x1x2₂+…+ r_x1xm_m

r_x2y= r_x2x1₁+₂+…+ r_x2xm_m

…

r_xmy= r_xmx1₁+r_xmx2₂+…+_m

(т.к. )

Найденные из данной системы –коэффициенты позволяют определить значения коэффициентов регрессии в естественном масштабе по формулам: , j=1;m; .

Значения коэффициентов корреляции берут из корреляционной матрицы - матрице парных линейных коэффициентов корреляции :

где r_jk – коэффициент парной линейной корреляции между j-ым и k-ым факторными признаками (j,k=1;m);

r_yj - коэффициент парной линейной корреляции между результативным признаком- y и j-ым фактором (j=1;m).

Коэффициент корреляции, измеряющий связь признака с самим собой, равен единице, т.к. в этом случае имеет место максимально тесная связь. Поэтому на главной диагонали в корреляционной матрице стоят единицы. Корреляционная матрица является симметричной относительно главной диагонали, т.к. r_jk=r_ki.

* Пример. Найдем коэффициенты регрессии через –коэффициенты (по данным о магазинах). Система нормальных линейных уравнений (в случае двух факторов) будет иметь вид:

r_x1y=₁+r_x1x2₂

r_x2y= r_x2x1₁+₂

Рассчитаем коэффициенты линейной парной корреляции и построим корреляционную матрицу: