Метод последовательных разностей

Метод последовательных разностей (МПР) используется для подбора неслучайной составляющей временного ряда (в частности локального аппроксимирующего полинома степени p). МПР основан на следующем математическом факте: если анализируемый временной ряд x(t) содержит в качестве неслучайной составляющей алгебраический полином x’(t)=порядкаp, то переход к последовательным разностям, повторенный p+1 раз (порядка p+1), исключает неслучайную составляющую, включая ₀, оставляя компоненты, выражающиеся только через случайную составляющую u(t).

Процедура

Имеется ряд x(1), x(2), …, x(T). Введем

…

где - число сочетаний изk элементов по i.

Теперь мы можем обсудить способ подбора полинома порядка p, представляющего собой неслучайную составляющую F(t) в разложении анализируемого ряда x(t).

Преобразование Бокса-Дженкинса

Автокорреляция остатков первого порядка, выявляемая с помощью статистики Дарбина-Уотсона, говорит о неверной спецификации уравнения либо о наличии неучтенных факторов. Естественно, для её устранения нужно попытаться выбрать более адекватную формулу зависимости, отыс­кать и включить важные неучтенные факторы или уточнить период оценивания регрессии. В некоторых случаях, однако, это не даст результата, а отклонения е_t просто связаны авторегрессионной зави­симостью. Если это авторегрессия первого порядка, то её формула имеет вид ( - коэффициент авторегрессии, (||<1), и мы предполагаем, что остатки _t в этой формуле обладают нужными свойствами, в частности - взаимно независимы. Оценив , введем новые переменные , (это преобразование называется авторегрессионным (AR), или преобразованием Бокса-Дженкинса). Пусть мы оцениваем первоначально формулу линей­ной регрессии . Тогда

Если величины e’_t действительно обладают нужными свойствами, то в линейной регрессионной зависимости авто­корреляции остатков e’_t уже не будет, и статистика DW окажется близкой к двум. Коэффициент b₁ этой формулы принимается для исходной формулы непосредственно, а коэффициент b₀

рассчитывается по формуле .

Оценки коэффициентов b₀ и b₁ нужно сравнить с первоначальными оценками, полученными для расчета отклонений е_t. Если эти оценки совпадают, то процесс заканчивается; если нет - то при новых значениях b₀ и b₁ вновь рассчитываются отклонения е_t до тех пор, пока оценки b₀ и b₁ на двух соседних итерациях не совпадут с требуемой точностью.

В случае, когда остатки e’_t также автокоррелированы, авторегрессионное преобразование может быть применено еще раз. Это означает использование авторегрессионного преобразования более высокого порядка, которое заключается в оценке коэффициентов авто­регрессии соответствующего порядка для отклонении е_t и использовании их для построения новых переменных. Такое преобразование вместо АR(1) называется АR(s) - если используется авторегрессия порядка s.

О целесообразности применения авторегрессионного преобразо­вания говорит некоррелированность полученных отклонений e’_t. Однако даже в этом случае истинной причиной первоначальной автокорреляции остатков может быть нелинейность формулы или неучтенный фактор. Мы же, вместо поиска этой причины, ликви­дируем ее бросающееся в глаза следствие. В этом - основной недостаток метода АR и содержательное ограничение для его применения.

Во многих случаях сочетание методов АR и MA позволяет решить проблему автокорреляции остатков даже при небольших s и q. Еще раз повторим, что адекватным такое решение проблемы является лишь в том случае, если автокорреляция остатков имеет собственные внутренние причины, а не вызвана наличием неучтенных (одного или нескольких) факторов.

Методы АR и MA могут использоваться в сочетании с переходом от объемных величин в модели к приростным, для которых статистическая взаимосвязь может быть более точной и явной. Модель, сочетающая все эти подходы, называется моделью АRIMA. В общем виде ее формулу можно записать так

где {_t} и {_t} - неизвестные параметры, и _t - независимые, оди­наково нормально распределенные случайные величины с нулевым средним. Величи­ны у* представляют собой конечные разности порядка d величин у, а модель обозначается как АRIMA(p,d,q).

Преобразования АR, MA и модель АRIMA полезно использовать в тех случаях, когда уже ясен круг объясняющих переменных и общий вид оцениваемой формулы, но в то же время остается сущес­твенная автокорреляция остатков. В качестве примера укажем оце­нивание производственных функции, где объясняющими перемен­ными служат используемые объемы или темпы прироста труда и капитала, а требуемой формулой является, например, производственная функция Кобба-Дугласа или СЕS.

Специфика изучения взаимосвязей по временным рядам. Исключение сезонных колебаний. Исключение тенденции.

Предположим, изучается зависимость между рядами Х_t и Y_t.

При моделировании взаимосвязи двух или более временных рядов могут возникнуть следующие проблемы:

1) Искажение показателей тесноты и силы связи (проблема «ложной корреляции»)::

• если ряды содержат циклические или сезонные колебания одинаковой периодичности, то это приведет к завышению истинных показателей тесноты связи изучаемых временных рядов;

• если только один из рядов содержат циклические или сезонные колебания или периодичность колебаний различна, то это приведет к занижению истинных показателей тесноты связи изучаемых временных рядов.

• если ряды имеют тренды одинаковой направленности, то между уровнями этих рядов всегда будет наблюдаться положительная корреляция, независимо от того существует ли причинная связь между этими рядами или нет;

• если ряды имеют тренды разной направленности, то корреляция рядов окажется отрицательной;

Для того чтобы избавиться от данных проблем необходимо устранить в уровнях ряда трендовый и сезонный (циклический) компоненты.

Устранить сезонный компонент в случае аддитивной модели можно оценив абсолютные разности- Sа_i (i=1;L, где L-число сезонов) и вычтя их из исходных уровней ряда. В случае мультипликативной модели необходимо оценить индексы сезонности – Is_i (i=1;L, где L-число сезонов) и разделить исходные уровни ряда на них. Как рассчитать сезонные компоненты смотри в статистике.

Устранение тенденции из уровней ряда.

1. Метод отклонений от тренда. При этом вычисляют значения u_xt, u_yt , представляющие собой отклонения уровней Х_t и Y_t от их значений, рассчитанных по уравнениям трендов: X’_t=f(t) и Y’_t=f(t): u_xt=X_t-X’_t , u_yt=Y_t-Y’_t. Затем измеряют корреляцию между этими отклонениями (u_x и u_y ), например, с помощью коэффициента корреляции:

r_ux,uy=.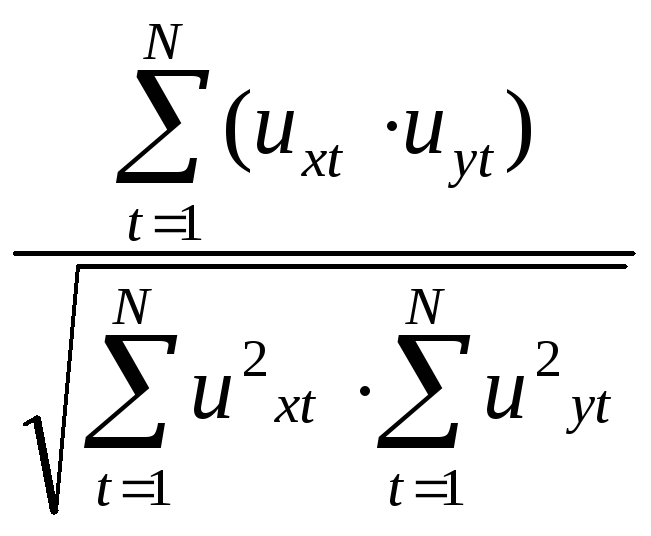

Если предполагаемая функция регрессии линейная, то можно построить уравнение регрессии, измеряющее зависимость отклонения u_y от отклонения u_x : u_y =а+ b·u_x. Параметры данного уравнения могут быть оценены с помощью МНК по формулам: b=;a= =0. Т.е. уравнение имеет вид:u_y =b·u_x .

Содержательная интерпретация параметра этой модели затруднительна. Так параметр b показывает, насколько в среднем за период отклонилось значение Y от тренда при отклонении Х от своего тренда на 1 ед. измерения.

Однако данное уравнение регрессии можно использовать для прогнозирования. Для этого необходимо определить трендовое значение факторного признака – Х’ и оценить величину предполагаемого отклонения фактического значения Х от трендового. Далее определяют по уравнению тренда Y значение Y’. По уравнению регрессии отклонений от трендов находят величину u_yt=Y_t-Y’_t. Затем находят точечный прогноз фактического значения Y_t+1 по формуле: Y_t+1=Y’_t+u_yt

2) Метод последовательных разностей. При этом вычисляют разности между текущим и предыдущим уровнями, т.е. величины абсолютных цепных приростов: y_t=Y_t-Y_t-1; x_t=X_t-X_t-1.

Тогда показатель тесноты связи – коэффициент линейной корреляции абсолютных приростов будет выглядеть так:

r_y,x =.

Уравнение регрессии по абсолютным приростам будет иметь вид:

y_t=а+ b·x_t

В отличие от уравнения регрессии по отклонениям параметрам данного уравнения (по абсолютным разностям) легко дать интерпретацию. Параметр b показывает прирост Y в среднем при изменении прироста Х на 1 единицу измерения. Параметр а характеризует прирост Y при нулевом приросте Х.

Недостатком данного метода является сокращение числа пар наблюдений, т.е. потеря информации.

Разности первого порядка исключают автокорреляцию только в тех рядах динамики, в которых основной тенденцией является прямая линия.

Для рядов, с основной тенденцией близкой к экспоненте, следует рекомендовать исследовать корреляцию цепных коэффициентов (темпов) роста.

Для рядов, с основной тенденцией близкой к параболе 2-ого порядка, следует рекомендовать исследовать корреляцию конечных разностей второго порядка: ²y_t=y_t -y_t-1; ²x_t=x_t-x_t-1.

Если ряды динамики имеют разные типы тенденций, вполне допустимо коррелировать соответствующие разные цепные показатели: например, абсолютные изменения в одном ряду с темпами изменений в другом.

3. Включение в модель регрессии фактора времени. При этом в уравнение регрессии включают переменную времени в качестве дополнительного фактора: Y=f(X,t). Например, Y_t=a+b·X_t+t+u_t. Преимущество данного метода в том, что модель регрессии, построенная таким образом, позволяет учесть всю информацию. Кроме того, интерпретация параметров не вызывает затруднений.