Проверка гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений (критерий Чоу)
Проведем теперь проверку значимости коэффициентов при фиктивных переменных.
Способом проверки существенности введенной фиктивной переменной выступает критерий Чоу, основанный на F-статистике. Проверяется гипотеза о совпадении уравнений регрессии для отдельных групп наблюдений (например, для мирного и военного времени из рассмотренного примера). Таким образом, с помощью теста Чоу можно ответим на вопрос: стоит ли разбивать совокупность на подгруппы или нет.
Пусть имеются две выборки, содержащие, соответственно, п1 и п2 наблюдений. Для каждой из этих выборок оценено уравнение регрессии вида
1=
01+
11х1
+
21х2
+ ... +
m1хm
и
=
02+
12х1
+
22х2
+ ... +
m2хm
Пусть
суммы квадратов отклонений уi
от линий регрессии равны для них,
соответственно,
и
.
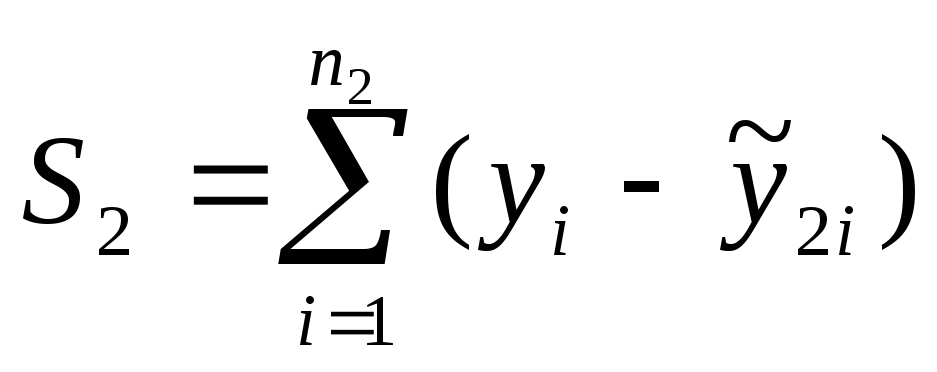Проверяется нулевая гипотеза, заключающаяся
в том, что все соответствующие коэффициенты
этих уравнений равны друг другу, то
есть, что уравнение регрессии для этих
выборок одно и то же. Пусть оценено
уравнение регрессии того же вида сразу
для всех (n1+n2)
наблюдений:
у
=
0+
1х1
+
2х2
+ ... +
mхm,
и сумма квадратов отклонений уi
от линии
регрессии равна для него S0.
Тогда рассчитывается F-статистика
по формуле
.
Она имеет распределение Фишера с (т+1, n-2m-2) степенями свободы. F-статистика будет близкой к нулю, если уравнение регрессии для обеих выборок одинаково, поскольку в этом случае S0= S1 + S2. Если же ее расчетное значение велико (то есть больше критического значения при данном уровне значимости), то нулевая гипотеза отвергается. Описанная процедура важна для ответа на вопрос, можно ли за весь рассматриваемый в модели период времени построить единое уравнение регрессии, или же нужно разбить его на части и на каждой из частей строить свое уравнение регрессии.