Устранение автокорреляции случайных составляющих.

Что можно сделать в отношении автокорреляции?

Во-первых, определить фактор, ответственный за автокорреляцию, и включить его в уравнение регрессии или изменить форму связи.

Во-вторых, построить уравнение регрессии не для исходных переменных y и x, а для их конечных разностей 1-го порядка Δy_t=y_t-y_t-1 и Δx_t=x_t-x_t-1.

В-третьих, в случае автокорреляции, подчиненной авторегрессионному процессу 1-ого порядка (т.е. u_t=·u_t-1+_t ,  t=1;n), мы могли бы полностью устранить автокорреляцию, если бы знали величину .

Предположим, что истинная модель задается выражением:

y_t= b₀ + b₁·x_t+u_t (*) (t=1;n).

Тогда наблюдение (t-1) формируется как: y_t-1=b₀+ b₁·x_t-1 +u_t-1.

Умножим полученное выражение на  и вычтем его из обеих частей уравнения (*). В результате получим:

y_t-·y_t-1=(1-)b₀+b₁(x_t-x_t-1)+u_t-·u_t-1.(**)

y^*_t = b*₀ +b₁· x^*_t + _t

Обозначим y^*_t=y_t-·y_t-1 ; x^*_t=x_t-·x_t-1, b*₀=(1-)b₀, _t= u_t-u_t-1 (t=2;n).

Значения _t (случайной составляющей в модели зависимости u_t от u_t-1) для различных t не зависят друг от друга, поэтому проблемы автокорреляции остатков в полученном уравнении для преобразованных переменных нет. Параметры данного уравнения оцениваются обычным МНК. Получаем оцененную регрессию: y^*’_t= ^*+ ·x^*_t.

Затем определяем оценку =^*/(1- ) и окончательно оцененное исходное уравнение регрессии: y’_t=+·x_t.

Однако, если в выборке нет данных предшествующих 1-ому наблюдению, мы не можем вычислить значения y^*₁, x^*₁. Уменьшение числа степеней свободы на единицу приведет к потере эффективности, которая может в небольших выборках перевесить повышение эффективности от устранения автокорреляции. Эту проблему решают с помощью поправки Прайса-Уинстена: y^*₁=·y₁, x^*₁=·x_1.

На практике величина  конечно неизвестна, его оценка получается одновременно с оценками параметров b₀ и b₁. В качестве оценки  обычно используют выборочный коэффициент автокорреляции остатков 1-ого порядка r_et,et-1:  = r_et,et-1.

(r_et,et-1=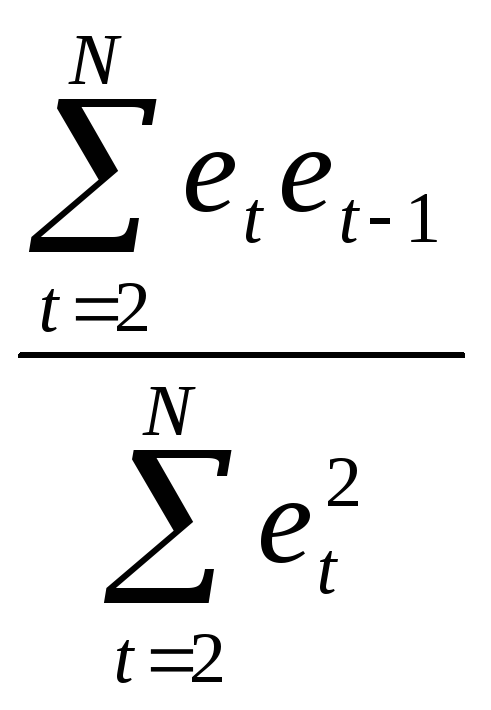,e_t=y_t-(+x_t),где ,–МНК-оценки параметровb₀, b₁).

Другой способ оценки  используется в методе Кохрейна-Оркатта. Алгоритм метода Кохрейна-Оркатта носит итеративный характер:

1) обычным МНК оценивается регрессия y⁽¹⁾’_t=⁽¹⁾+⁽¹⁾·x_t (*);

2) вычисляются остатки e_t⁽¹⁾=y_t - y⁽¹⁾’_t (t=1;n);

3) оценивается регрессионная зависимость e^(k)_t от e^(k)_t-1: e’^(k)_t=^*(k)·e^(k)_t-1, коэффициент при e^(k)_t-1 равный ^(k)* представляет собой оценку , k –номер итерации;

4) с этой оценкой (^(k)*) уравнение (*) преобразуется к виду:

y^*(k)_t= b*^(k)₀+ b₁·x^*(k)_t+u^*(k)_t (**),

где y^*(k)_t=y_t-^*(k)·y_t-1; b*^(k)₀=(1-^*(k))b₀; х^*(k)_t=х_t-^*(k)·х_t-1; u^*(k)_t=u_t- ^*(k)·u_t-1.

5) обычным МНК оценивается уравнения (**): y^*(k)’_t= *^(k) +^(k)·x^*(k)_t. Затем вычисляют оценку параметра ^(k) =*^(k)/(1-^*(k)).

6) повторно вычисляются остатки e_t и процесс возвращается к этапу 3.

Процесс обычно заканчивается, когда очередное приближение ^*(k) мало отличается от предыдущего ^*(k-1). Иногда просто фиксируется количество итераций.

Еще один способ оценки - метод Хилдрета-Лу:

Для каждого значения  из определенного диапазона с заданным шагом внутри (например, =-1; 1; 0,01) его оценивается преобразованное уравнение регрессии:

y^*_t= b₀^*+ b₁·x^*_t+u^*_t (**),

где y^*_t=y_t-^*·y_t-1; b^*₀=(1-^*)b₀; х^*_t=х_t-^*·х_t-1; u^*_t=u_t- ^*·u_t-1.

Значение , которое дает минимальную сумму квадратов отклонений для преобразованного уравнения (**), принимается в качестве оценки . Оценка параметра исходного уравнения регрессии (*) : =*/(1-^*).

Обобщенный метод наименьших квадратов- ОМНК (GLS).

Обобщенный метод наименьших квадратов (ОМНК) применяется в том случае, если нарушена третья, либо четвертая предпосылки нормальной линейной регрессионной модели, т.е. если случайные составляющие не имеют постоянной дисперсии или коррелированы между собой. Это характерно для неоднородной совокупности, состоящей из сильно отличающихся друг от друга единиц.

В этом случае имеет место обобщенная линейная модель множественной регрессии, которая в матричной форме выглядит так:

Y=X·b+U

X - неслучайная матрица, имеющая полный ранг, т.е. х₁, х₂, …, х_m – неслучайные переменные.

M(U)=0ⁿ

С_U=_u²C₀, где C₀ – некоторая заранее известная матрица.

Основное отличие обобщенной регрессионной модели от нормальной состоит в виде матрицы ковариации случайных составляющих – С_U. В нормальной модели предполагается, что матрица С₀ равна единичной матрице. В обобщенной модели допускается, что ковариации (следовательно, дисперсии и корреляции) остатков могут быть произвольными, следовательно, и матрица С₀ может содержать произвольные значения. В этом – суть обобщения нормальной модели.

Применение традиционного (обычного) МНК к обобщенной регрессионной модели дает состоятельные и несмещенные оценки. Однако данные оценки становятся неэффективными. Поэтому для оценивания параметров обобщенной модели пользуются обобщенным МНК. При этом вектор оценок параметров модели определяется по формуле:

=(X^T·C₀^-1·X)^-1 X^T ·C₀^-1·Y (*).

Следует отметить, что для обобщенной регрессионной модели, в отличие от нормальной, коэффициент детерминации R² не может служить удовлетворительной мерой качества модели. Он даже не обязан лежать в интервале от 0 до 1, а добавление или удаление независимой переменной не обязательно приводит к его увеличению или уменьшению.

Проверка гипотез о значимости коэффициентов регрессии проводится также как и в случае нормальной линейной модели.

Ковариационная матрица МНК-оценок параметров регрессии (которая используется для определения дисперсий и стандартных ошибок оценок параметров) будет рассчитываться как: =σ_u²(X^T·C₀^-1·X)^-1.

В отличие от нормальной модели в рамках обобщенной модели регрессии σ_u² уже нельзя интерпретировать как величину дисперсии случайной составляющей. Однако для получения ковариационной матрицы МНК-оценок его нужно оценить. Для его оценки используют следующую формулу:

.

Для применения ОМНК необходимо знать матрицу С_U, что на практике бывает редко. Рекомендуется оценить каким-либо образом матрицу С_U, а затем использовать эту оценку в формуле (*) вместо С_U. Для этого вводят априорные ограничения на структуру матрицы С_U. Данный подход составляет суть так называемого доступного обобщенного метода наименьших квадратов (FGLS) и используется при оценивании параметров в модели с гетероскедастичностью, а также в случае автокорреляции случайных составляющих.

Рассмотрим ковариационную матрицу случайных составляющих в случае их гетероскедастичности и взаимной независимости. Если предположить, что _ui приблизительно пропорциональна х_i, т.е. x_i=·_ui, то ковариационная матрица может быть представлена в виде:

С_u= =.

Рассмотрим ковариационную матрицу случайных составляющих в случае их автокорреляции. При сохранении свойства гомоскедастичности и в предположении, что случайные составляющие связаны автокорреляционной зависимостью 1-ого порядка: u_t=·u_t-1+_t, ковариационная матрица может быть представлена в виде:

С_u=.

Напомним, что .

15