1.5. Плоская система произвольно расположенных сил

Задача приведения системы произвольно расположенных сил к простейшему виду связана с необходимостью их переноса по плоскости параллельно самим себе. Рассмотрим предварительно теорему о возможности такого переноса.

Теорема о параллельном переносе силы (теорема Пуансо).

Пусть в точке А тела приложена сила , которую требуется перенести самой себе в точкуВ (рис. 16,а). Приложим в точке В уравновешенную систему из двух сил и, равных и параллельных(рис. 16,б). Тогда силуможно считать силой, перенесенной в точкуВ, а силы и, образуют пару с моментомM=Fh. Таким образом, состояние, изображенное на рис. 16,в, соответствует первоначальному состоянию тела.

а) б) в)

Рис. 16

Итак, не изменяя действия силы на тело, ее можно перенести в любую точку параллельно самой себе, добавив пару сил, момент которой равен моменту заданной силы относительно новой точки приложения (рис. 16,в).

1. Приведение плоской системы сил к данной точке.

Пусть на твердое тело действует произвольная плоская система ,,(рис. 17,а).

а) б) в) г)

Рис. 17

Выберем произвольную точку О – центр приведения. Перенесем все силы в точку О, добавляя при этом соответствующие пары. В результате приведения получим систему сил ,,…и систему парM₁=F₁h₁, M₂=F₂h₂, …, M_n=F_nh_n (рис. 17,б).

Силы, приложенные в точке, можно заменить одной силой, равной их векторной сумме, – главным вектором F_p (рис. 17,в)

(8)

Моменты, действующие на тело, можно заменить одним моментом, равным их алгебраической сумме, – главным моментом:

(9)

Таким образом, произвольную плоскую систему сил всегда можно заменить главным вектором и главным моментом (рис. 17,г).

2. Условия равновесия произвольной плоской системы сил.

Произвольная плоская система сил находится в равновесии, если главный вектор и главный момент этой системы относительно любой точки равны нулю, т.е.

, (10)

Первое равенство эквивалентно двум равенствам:

;

Итак, для равновесия тела, находящегося под действием произвольной плоской системы сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра равнялась нулю. Уравнения равновесия произвольной плоской системы сил:

;;(11)

Возможны и другие формы записи уравнений равновесия:

; ;(12)

где ось X не должна быть перпендикулярна линии АВ. Или

; ;(13)

где точки А, В и С не должны лежать на одной прямой.

1.6. Примеры решения задач

В рассмотренных ниже примерах необходимо найти реак­ции связей. Решения приводятся в общем виде (без численных значений).

Задача 1.

Определить реакции стержней кронштейна, приведенного на рис. 18,а. Дано: F, , .

а) б)

Рис. 18

Объект равновесия – узел А. Отбрасываем стержни и заменяем их действие соответствующими реакциями R₁ и R₂ (рис. 18,б). Записываем два уравнения равновесия:

; (14)

; (15)

Решая эту систему уравнений, находим реакциями R₁ и R₂.

Задача 2.

Найти полную реакцию неподвижного цилиндрического шарнира А и реакцию в стержне ВС, удерживающих в равновесии тело прямоугольной формы (рис. 19,а). Дано: F, а, b.

а) б)

Рис. 19

Объект равновесия – тело прямоугольной формы. Отбрасываем связи (шарнир А и стержень ВС) и заменяем их действие соответствующими реакциями R_AX, R_AY и R_BC (рис.19,б). Первые два уравнения равновесия будут иметь вид:

; (16)

;; (17)

В качестве третьего уравнения равновесия запишем сумму моментов всех сил относительно точки А:

; (18)

Необходимые для решения этих уравнений величины находятся следующим образом:

; ; (19)

Решая эту систему уравнений находим R_AX, R_AY и R_BC. Тогда

(20)

Для проверки решения задачи можно использовать уравнение суммы моментов всех сил относительно любой другой точки тела, например, В:

(21)

Если задача решена верно, то это уравнение будет равно нулю.

Задача 3.

Невесомая балка опирается на две опоры – цилиндрический неподвижный шарнир в точке А и подвижный шарнир в точке В (рис. 20,а). Необходимо найти реакции в этих опорах, если даны: F, q, М , а, b, с.

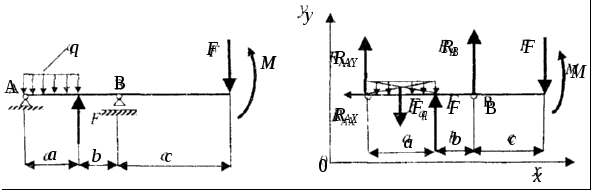
а) б)

Рис. 20

Объект равновесия – балка. Отбрасываем связи (шарниры в точках А и В) и заменяем их соответствующими реакциями R_AX, R_AY и R_BC (рис.20, б).

Первые два уравнения равновесия будут иметь вид:

; (22)

; ,где .(23)

В качестве третьего уравнения равновесия запишем сумму моментов всех сил относительно точки А:

; (24)

Решая эту систему уравнений, находим R_AX, R_AY и R_BC. Для проверки решения задачи можно использовать уравне­ние суммы моментов всех сил относительно точки В:

. (25)

Если задача решена верно, то это уравнение будет равно нулю.

Задача 4.

Горизонтальный стержень жестко защемлен одним концом в точке А (рис.21,а). Найти реакции в этой точке, если дано: F, М, q, а, b, .

а) б)

Рис. 21

Объект равновесия – горизонтальный стержень. Отбрасываем связь (жесткая заделка в точке А) и заменяем ее соответствующими реакциями R_AX, R_AY и M_А (рис 21,б). Составляем три уравнения равновесия:

; , (26)

; , (27)

где F_q1=qa; F_q2=qb;

; , (28)

где h=asin.

Решая эту систему уравнений, находим R_AX, R_AY и M_А. Тогда .

Для проверки решения задачи составляем уравнение суммы моментов всех сил относительно точки В:

(29)

Если задача решена верно, то уравнение (29) будет равно нулю.