2.2. Пример решения задачи
Построить графики изменения поперечной силы Q изгибающего момента М по длине элемента, показанного на рис. 5,а. Определить размеры его прямоугольного сплошного поперечного сечения при отношении высоты сечения к ширине равным 2, если допускаемые напряжения материала элемента при деформации изгиба [u] известны.
Отбросив связи в точках А и В, покажем соответствующие реакции RА, RBX и RBY (рис. 5,б).
Запишем уравнения равновесия, из которых найдем значения этих реакций:
;
(10)
;
;
кН
(11)
;
;
кН (12)
Рассмотрим
первый участок. Проведем произвольное
сечение на расстоянии х
от
левого конца элемента. Рассмотрим левую
от сечения часть (рис. 5,в). Покажем
внутренние силовые факторы
Q1
и М1
в сечении, причем их направления примем
в соответствии с рис.4. Составим уравнения
равновесия для рассматриваемой части:
сумму проекций сил на вертикальную ось
и сумму моментов относительно точки
оси, через которую проходит проведенное
сечение:
;
;
кН;
(13)
;
;
(14)
а)
б)
в)
|
г) |
д)
|
Рис. 5
Таким образом, поперечная сила во всех сечениях первого участка одинакова, а момент изменяется по линейному закону. Построим по этим зависимостям фрагменты графиков Q и M, причем последний построим по двум значениям (рис. 6,а и рис. 6,б):
Рис. 6
;
Нм
Рассмотрим второй участок. Расчетная схема для определения <2 и М показана на рис. 5,г. Выполняя те же действия, что и для первого участка, получим:
;
;
кНм
(15)
;
;
(16)
Подставляя в выражение момента координаты начала и конца второго участка, получим:
Нм;
Нм
Построим по этим решениям графики Q и М для второго участка.
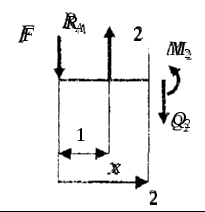
Рассмотрим третий участок. Показав на нем произвольное сечение, очевидно, что для определения Q и М целесообразно выделить правую часть (рис. 5,д). Положительные направления внутренних усилий для правой части приняты в соответствии с рис. 4. Расстояние до сечения будем отсчитывать от точки В. Составляя уравнение равновесия, получим
;
;
(17)
;
;
(18)
На этом участке Q изменяется по линейному закону (рис. 6,а), а М – по квадратичному закону (график М - парабола: рис. 6,б). Подставляя в выражения Q и М координаты крайних сечений этого участка, получим
кН;
кН.
;
кНм (19)
Для более точного построения графика М вычислим дополнительно значение в середине участка: при х=1, М=7 кНм.
Определим значение Мmax.Для этого предварительно найдем координату сечения, в котором М=Мmах, приравняв нулю производную от М по х.
.
откуда х=1,67 м.
Тогда
кНм
Построенные графики обладают следующими общими свойствами, которые могут быть использованы для проверки правильности их построения:
1. если на участке элемента отсутствует распределенная нагрузка, то график Q – прямая, параллельная оси абсцисс, а график моментов М – наклонная прямая;
2. если на участке элемента имеется равномерно распределенная нагрузка, то график Q – наклонная прямая, а график М – парабола;
3. изгибающий момент имеет экстремальное значение в том сечении, в котором поперечная сила равна нулю;
4. если распределенная нагрузка направлена вниз, то парабола, представляющая собой график М, обращена выпуклостью вверх, т.е. навстречу нагрузке, и наоборот;
5. под сосредоточенной силой на графике Q имеет место «скачок», величина которого равна приложенной силе, а на графике М – изменение угла наклона (излом) смежных участков графика;
6. там, где к элементу приложена сосредоточенная пара сил, на графике М – имеет место «скачок», равный моменту этой пары.
Из равенства (7) по найденному значению Мmах=8,33 кНм может быть рассчитан момент сопротивления поперечного сечения
(20)
Учитывая заданное соотношение размеров сечения h=2b, подставляя его в уравнение (51), выражаем b
.