1.2. Пример решения задачи

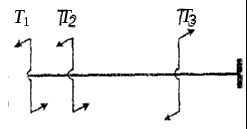
Для вала, изображенного на рис. 1,а построить график изменения величины крутящего момента T_k по его длине и определить диаметр d, если допускаемые напряжения [_k] известны.

Используя результаты, полученные в подразделе 1.1 при расчетах T_k1, T_k2 и T_k3, а также тот факт, что значения этих моментов не зависят от места проведения сечения на соответствующем участке, т.е. являются постоянными по длине этого участка, строим требуемый в условиях задачи график (рис. 2).

Рис. 2

На данном графике видно, что в местах приложения внешних скручивающих моментов T получаются скачкообразные изменения ординат. Размер «скачка» равен приложенному в соответствующем месте вала скручивающему моменту. Этот факт может использоваться для проверки правильности построения данного графика.

Из рис. 2 следует, что в данной задаче максимальный крутящий момент

Диаметр вала d определяем по зависимости (6), используя найденное значение Т_k^max и известные допускаемые напряжения [_k].

1.3. Задачи для самостоятельной работы

Задача 7

Для вала сплошного поперечного сечения, нагруженного тремя заданными внешними закручивающими моментами, требуется:

1. используя уравнения равновесия, найти момент T₀ для вала, установленного в двух опорах) или момент Т₃ в заделке (для вала, защемленного одним концом);

2. в выбранном масштабе построить график изменения крутящего момента по длине вала;

3. исходя из условия прочности при кручении, вычислить требуемый диаметр вала и округлить полученный результат до величины кратной 10 мм. Допускаемые напряжения материала вала при кручении принять равным 80 МПа.

Исходные данные приведены в табл. 1 и табл. 2.

Таблица 1

Численные данные	Предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
T1, кНм	0	70	35	30	60	30	20	40	60	60
T2, кНм	0	80	70	60	80	50	20	30	50	50
T3, кНм	0	80	50	40	40	20	30	40	20	20

Таблица 2

Посл. цифра шифра	Расчетная схема	Посл. цифра шифра	Расчетная схема
0		5

Окончание табл. 14

Посл. цифра шифра	Расчетная схема	Посл. цифра шифра	Расчетная схема
1		6
2		7
3		8
4		9

Задача № 2 деформации и напряжения при изгибе

2.1. Основные сведения

Изгибом называют деформацию элемента, связанную с искривлением его оси под действием пар сил или поперечных нагрузок (рис. 3).

а) б)

Рис. 3

Элементы, работающие на изгиб, называют балками. Деформацию изгиба испытывают многие элементы машин и конструкций, например, ось, поддерживающая вращающие детали и машины, элементы рамы автомобиля, балки перекрытий или мостовых конструкций.

При изгибе в поперечных сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент M. Если поперечная сила равна нулю, то изгиб называют чистым.

Поперечная сила Q обусловлена действием касательных напряжений , а изгибающий момент – действием нормальных напряжений _u.

В подавляющем большинстве случаев касательные напряжения при деформации изгиба невелики, поэтому расчет на прочность проводится по нормальным напряжениям.

Внутренние силовые факторы определяют с помощью метода сечений. Они зависят как от внешних активных сил, так и реакций связей. Поэтому до определения внутренних сил с помощью уравнений равновесия должны быть найдены все реакции связей.

Для расчета на прочность необходимо определить максимальные значения внутренних силовых факторов и установить сечения, в которых они возникают (опасные сечения). Для наглядного представления о характере их изменения по длине элемента строят соответствующие графики поперечных сил и изгибающих моментов. Для построения графиков Q и M необходимо разбить элемент на участки. Границами участков являются места приложения сосредоточенных сил, пар сил (моментов), начало и конец линии действия распределенной нагрузки. Следуя методу сечений, необходимо рассмотреть часть балки по одну сторону от интересующего нас сечения, приложить заданные нагрузки и реакции связей, действующие на эту часть, и внутренние силовые факторы (Q и M) в сечении. Из уравнений равновесия, составленных для отсеченной части, определяются значения Q и M.

В соответствии с характером деформации элемента примем следующие правила знаков: поперечная сила Q считается положительной, если она стремиться повернуть элемент по часовой стрелке; изгибающий момент M считается положительным, если элемент изгибается выпуклостью вниз.

На рис. 4 приведены левая и правая отсеченные части элемента и показаны направления Q и M, принятые за положительные.

Рис. 4

Во избежание путаницы со знаками рекомендуется на расчетной схеме в зависимости от рассматриваемой отсеченной части показывать направления внутренних силовых факторов в соответствии с рис. 4.

Условия прочности по нормальным напряжениям при деформации изгиба записывается в виде:

(7)

где – максимальные нормальные напряжения;

M^max – максимальный изгибающий момент (момент в опасном сечении элемента);

W_z – момент сопротивления поперечного сечения при деформации изгиба;

[_u] – допускаемые нормальные напряжения материала элемента при деформации изгиба.

Момент сопротивления поперечного сечения при изгибе определяется по следующим зависимостям:

- для сплошного прямоугольного сечения высотой h и шириной q:

(8)

- для круглого сплошного сечения диаметром :

(9)

При проектном расчете элемента, решая совместно (7), (8) и (9), находят его размеры.