Инх. Конспект лекций МРИ / Л.4 Конич.передачи / Л.4Конич.передачи (текст)

Лекция 5.Конические передачи.

Учебные вопросы:

1. Устройство и основные геометрические и силовые соотношения конических передач.

2. Расчет зубьев прямозубой конической передачи на изгиб.

3. Расчет конических прямозубых передач на контактную прочность.

4. Последовательность проектировочного расчета конической передачи.

1. Устройство и основные геометрические и силовые соотношения конических передач.

Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 3.45, с.96, Мархель) и служит для передачи вращающего момента между валами с пересекающимися осями под углом . Наиболее распространена в машиностроении коническая передача с углом между осями (рис. 3.47), но могут быть передачи и с . Колеса конических передач выполняют с прямыми (рис. 3.46, а), косыми (рис. 3.46, б), круговыми зубьями (рис. 3.46, в).

Передачу с коническими колесами для передачи вращающего момента между валами со скрещивающимися осями называют гипоидной (рис. 3.48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже цилиндрических при равных силовых параметрах. Их применение диктуется только необходимостью передавать момент при пересекающихся осях валов. Передаточное число одной пары .

Вершины начальных и делительных конусов конической передачи находятся в точке пересечения осей валов О (рис. 3.50, с.97, Мархель). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 3.47 и 3.50):

- делительный конус шестерни;

- делительный конус колеса;

- делительный дополнительный конус шестерни;

- делительный дополнительный конус колеса;

- угол делительного конуса шестерни;

- угол делительного конуса колеса;

- внешний делительный диаметр шестерни;

- внешний делительный диаметр колеса;

- средний делительный диаметр шестерни;

- средний делительный диаметр колеса;

- ширина зубчатого венца (длина зуба);

- внешнее делительное конусное расстояние (или длина дистанции).

Передаточное число конической передачи определяется так:

.

В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают только внешнюю и среднюю делительные окружности (см. рис. 3.47).

Из условия, что в конической передаче модуль и делительный диаметр связаны теми же соотношениями, что и в цилиндрических передачах, т.е. (рис. 3.51), определяют внешний и средний делительные диаметры:

; ,

где - внешний окружной модуль;

- средний окружной модуль.

Внешний окружной модуль обычно выбирают из стандартного ряда. Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубчатых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения).

Средний окружной модуль рассчитывают в зависимости от внешнего окружного модуля . По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Таблица 1

Геометрические параметры прямозубой конической передачи.

Параметр, обозначение	Расчетные формулы
Внешний окружной модуль	;
Средний окружной модуль
Внешний диаметр вершин зубьев
Внешний делительный диаметр
Внешний диаметр впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Окружной шаг
Радиальный зазор
Ширина зубчатого венца
Внешнее делительное конусное расстояние
Угол делительного конуса шестерни
Угол делительного конуса колеса

2. Расчет зубьев прямозубой конической передачи на изгиб.

Расчет производят по аналогии с расчетом цилиндрической прямозубой передачей.

Опытным путем установлено, что нагрузочная способность конической передачи ниже, чем цилиндрической. В соответствии с этим в расчетные формулы для зубьев конической передачи вводят коэффициент , учитывающий снижение их нагрузочной способности по сравнению с зубьями цилиндрических передач.

Расчет на прочность зубьев при изгибе производят по среднему значению модуля зубьев . Коэффициент формы зуба выбирают по аналогии с цилиндрической прямозубой передачей, но в зависимости от числа зубьев эквивалентных колес .

Под числом зубьев эквивалентных колес понимают такое число зубьев, которое может расположиться на длине окружности (см. рис. 3.47, Мархель) радиусом, равным длине образующей дополнительного конуса .

Вопрос: По какому модулю производят расчет геометрических параметров и по какому модулю – расчет на прочность конической передачи?

-Расчет геометрических параметров передачи производят по модулю , а на изгибную прочность - по .

Проверочный расчет следует проводить по аналогии с прямозубой передачей.

Расчетные напряжения изгиба в зубьях конических колес и условие прочности выражается формулой:

(3.31)

Здесь - коэффициент нагрузки при расчете не изгиб, выбираемый так же, как и для цилиндрических прямозубых колес; - коэффициент формы зубьев; - средний модуль; - окружная сила, которую считают приложенной по касательной к средней делительной окружности:

.

Допускаемое напряжение выбирают так же, как и для цилиндрических зубчатых колес.

Проектировочный расчет. Средний модуль зубьев определяется по формуле:

.

Коэффициент ширины венца по отношению к среднему модулю

.

.

3. Расчет конических прямозубых передач на контактную прочность.

Хотя расчет конических зубчатых передач ГОСТом еще не регламентирован, тем не менее целесообразно выполнять его, ориентируясь на зависимости, приведенные выше для цилиндрических зубчатых колес.

На основании формулы (3.6) используемой для проверочного расчета косозубых передач на выносливость по контактным напряжениям:

(3.6)

с учетом особенности геометрии конических зубчатых колес (рис. 3.4, с. 40 С.А.Чернавский) после соответствующих преобразований получают формулу для определения контактных напряжений при проверочном расчете конических прямозубых колес:

(3.27)

При расчете по среднему конусному расстоянию формула (3.27) принимает вид:

(3.28)

Здесь и - внешнее и среднее конусные расстояния, мм; - коэффициент нагрузки, принимаемый таким же, как и для цилиндрических прямозубых передач, при условии, что степень точности конических колес на единицу выше, чем цилиндрических; - вращающий момент на колесе, ; - ширина зубчатого венца, мм.

При проектном расчете определяют внешний делительный диаметр колеса:

(3.29)

Результат округляют по СТ СЭВ 229-75. Здесь коэффициент ширины зубчатого венца . При проектировании редукторов с параметрами по ГОСТ 12289-76 рекомендуется принимать .

Коэффициент нагрузки принимают предварительно для колес с твердостью поверхностей зубьев , при твердости .

При проверочном расчете значения уточняют.

Далее определяют числа зубьев колес. Для шестерни:

(3.30)

Рекомендуется выбирать .

Число зубьев колеса . Так как найденные значения и округляют до целых чисел, то после этого следует уточнить и угол arctg. Внешний окружной модуль ; округлять полученное значение не надо.

Остальные параметры передачи определяют по табл.1.

5. Последовательность проектировочного расчета конической зубчатой передачи.

1. Определить передаточное число и углы делительных конусов шестерни и колеса и .

2. В зависимости от условий работы передачи выбрать материалы колес, назначить термическую обработку и значения твердости рабочих поверхностей зубьев.

3. Определить допускаемые контактные напряжения и допускаемые напряжения изгиба .

4. Выбрать коэффициент длины зуба.

5. Определить внешний делительный диаметр из условия контактной прочности.

6. Задать число зубьев шестерни , определить число зубьев колеса .

7. Рассчитать средний модуль .

8. Определить числа зубьев эквивалентных колес и и по табл. – коэффициенты формы зуба шестерни и колеса .

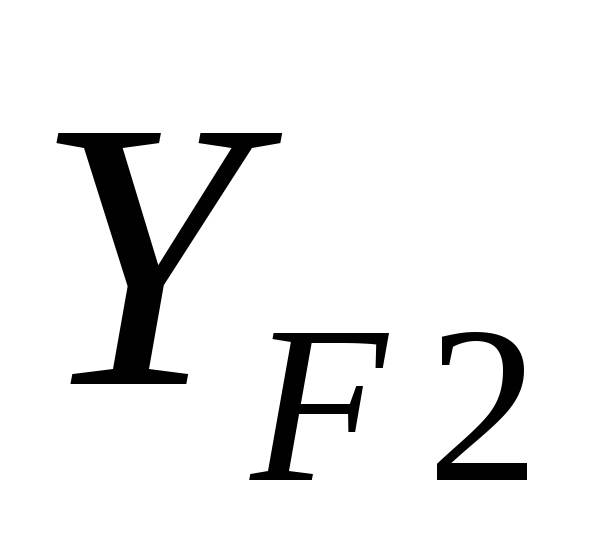9. Проверить прочность зубьев по напряжениям изгиба. Пир неудовлетворительных результатах (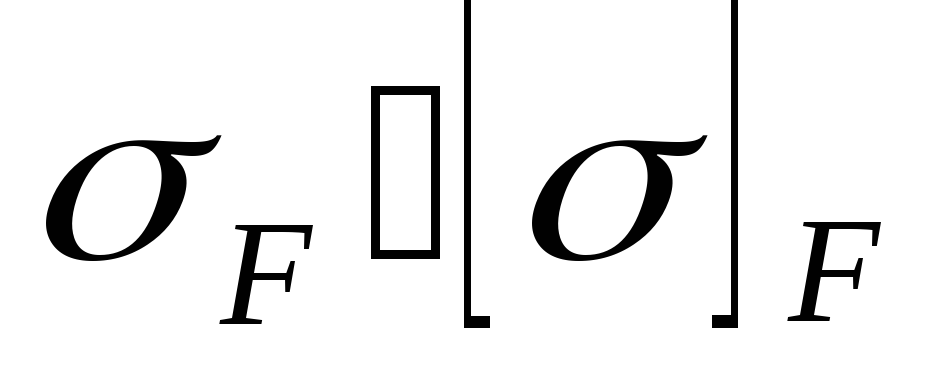) необходимо путем соответствующего изменения числа зубьев и модуля при том же конусном расстоянии добиться определенного изменения напряжений изгиба, не нарушая при этом условия контактной прочности.

10. Произвести геометрический расчет передачи (табл.1).

11. Определить окружную скорость колес и по табл. Назначить соответствующую степень точности.