механика.физика / стр.46-51

51

Импульсом системы принято называть векторную сумму импульсов всех тел, образующих систему

Радиус-вектор

центра масс

,

Для описания положения системы тел в пространстве вводится понятие "центр масс" (или "центр инерции"). Радиус-вектор , задающий положение центра масс системы относительно некоторой точки О, принятой за начало отсчета, определяется правилом

Рис. 37

m₁

m₂

m₃

C

O

,

п

ри этом радиусы-векторы, определяющие положение отдельных частей системы, должны отсчитываться от той же точки О (см. рис. 37).

Ц

ентры масс однородных тел (для которых плотность вещества одинакова во всех точках) совпадают с их геометрическим центром. Центр масс может лежать вне тела, например, центр масс однородного кольца – точка С (рис. 38).

1.3.2 Теорема о движении центра масс

Рис. 38

П

С

рименим основной закон динамики к описанию движения системы взаимодействующих тел, используя формулировку

с учетом того, что ускорение есть вторая производная радиуса-вектора по времени:

.

На каждое тело системы могут действовать как внутренние силы со стороны тел, образующих систему, так и внешние со стороны тел, не входящих в рассматриваемую систему. Для каждого из тел системы, представленной на рис.39, можно написать:

Рис. 39

2

Сложим эти уравнения с учетом III закона Ньютона.

1

,

т

огда сумма всех внутренних сил окажется равной нулю и

3

.

В правой части этого уравнения операции суммирования и дифференцирования можно поменять местами, поскольку они производятся по независимым переменным:

.

Умножив числитель и знаменатель на общую массу системы, получим

.

Согласно введенному ранее определению - радиус-вектор центра масс системы;

;

Теорема о движении центра масс

- ускорение центра масс системы, окончательно:

-

- теорема о движении центра масс. Можно дать несколько словесных формулировок полученной теоремы.

Первая формулировка: у с к о р е н и е ц е н т- р а м а с с с и с т е м ы о п р е д е л я е т с я т о л ь к о в н е ш н и м и с и л а м и, д е й с т в у ю щ и м и н а с и с т е м у.

Вторая формулировка: ц е н т р м а с с с и с - т е м ы д в и ж е т с я т а к, к а к д в и г а л а с ь б ы м а т е р и а л ь н а я т о ч к а, в к о т о р о й с о с - р е д о т о ч е н а в с я м а с с а с и с т е м ы, и к к о - т о р о й п р и л о ж е н ы в с е в н е ш н и е с и л ы, д е й с т в у ю щ и е н а с и с т е м у.

Третья формулировка: в н у т р е н н и е с и л ы н е м о г у т и з м е н и т ь с о с т о я н и е д в и ж е н и я ц е н т р а м а с с с и с т е м ы.

1.3.3 Законы сохранения в классической

механике

Законы сохранения импульса и момента

импульса

Применим основной закон динамики к описанию движения системы взаимодействующих тел, используя формулировку, - импульс силы, действующей на тело, равен изменению импульса тела, где под будем подразумевать равнодействующую всех внешних и внутренних сил, действующих на рассматриваемое тело системы. Для каждого из тел системы, представленной на рис. 39 можно написать:

.

Сложим эти уравнения. С учетом III закона Ньютона сумма импульсов всех внутренних сил будет равна нулю:

.

Поменяв местами операции суммирования и дифференцирования в левой части этого уравнения, получим:

-

- изменение суммарного импульса всех тел, образующих систему, равно сумме импульсов внешних сил, действующих на систему.

Если система замкнутая, то есть сумма внешних сил равна нулю , то

,

или

.

О

Закон сохранения импульса

,

если

ба последних выражения можно рассматривать как математическую запись закона сохранения импульса.

П р и л ю б ы х в з а и м о д е й с т в и я х т е л в н у т р и з а м к н у т о й с и с т е м ы в е к т о р н а я с у м м а и м п у л ь с о в т е л, о б р а з у ю щ и х с и с- т е м у, о с т а е т с я п о с т о я н н о й.

При решении задач закон сохранения импульса предпочтительнее выражать следующим образом:

-

- векторная сумма импульсов тел системы в первом состоянии (I) равна векторной сумме импульсов тел системы во втором состоянии, если при переходе системы из первого состояния во второе на систему не действовали внешние силы, или их векторная сумма оказалась равной нулю (то есть система оставалась замкнутой).

Р

Закон сохранения момента импульса

,

если

ассуждая аналогичным образом для вращательного движения и применяя к каждому из тел системы основное уравнение динамики в виде (импульс момента сил, действующих на тело равен изменению момента импульса тела), получим сначала, что - изменение суммарного момента импульса всех тел, образующих систему, равно сумме импульсов моментов внешних сил, действующих на систему.

Далее, рассматривая замкнутую систему, что в случае вращательного движения означает необходимость равенства нулю суммы моментов внешних сил, приходим к закону сохранения момента импульса. Математически этот закон может быть выражен любым из следующих уравнений:

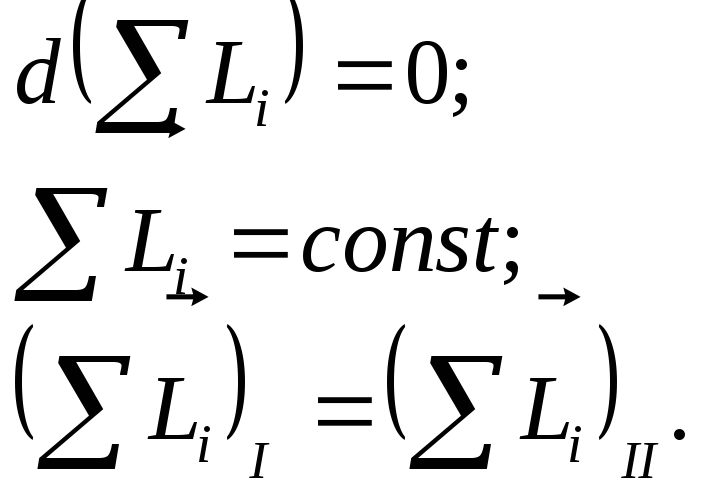
Закон сохранения механической энергии

Применим основной закон динамики к описанию движения системы двух взаимодействующих тел, используя формулировку (изменение кинетической энергии тела равно сумме работ всех сил, действующих на тело). Выделим три группы сил, которые могут действовать на тело: внешние, внутренние потенциальные и внутренние не потенциальные.

Для каждого из тел системы основное уравнение динамики примет вид

.

С

Полная механическая энергия

системы

кладывая эти уравнения и обозначая сумму работ каждого вида сил одним символом, получим:

.

Ранее было показано, что работа потенциальных сил равна убыли потенциальной энергии системы

,

т

Энергия

1 электрон-Вольт

1,610^-19 Дж

Энергия, поступающая от Солнца на Землю за 1 секунду 310¹⁷ Дж

Кинетическая энергия пули, вылетающей из ствола винтовки 0,510⁴ Дж

Кинетическая энергия -частицы, вылетающей из ядра атома радия при радиоактивном распаде

5 Мэ-В или 810^-13 Дж

Потенциальная энергия взаимодействия Луны и Земли 7,610²⁸ Дж

огда

,

где - полная механическая энергия системы. Изменение полной механической энергии системы определяется суммой работ внешних и внутренних не потенциальных сил. На основании полученного можно также утверждать, что действие потенциальных сил не приводит к изменению полной механической энергии системы. Если на тела системы действуют только потенциальные силы, то может происходить переход кинетической энергии в потенциальную и обратно, но механическая энергия при этом не переходит в другие виды (в тепловую и др). Эта особенность потенциальных сил была отмечена в разделе 1.6.

Рассмотрим замкнутую систему, на которую не действуют внешние силы, или работа этих сил равна нулю. Предположим, что эта система еще и консервативная, то есть между телами системы действуют только потенциальные силы, не потенциальных сил нет, либо их работа равна нулю, тогда

Закон сохранения механической

энергии

если

и

,

или

,

или

.

Любое из этих уравнений можно рассматривать как математическое выражение закона сохранения механической энергии.

П о л н а я м е х а н и ч е с к а я э н е р г и я с и с- т е м ы о с т а е т с я п о с т о я н н о й, е с л и с и с т е- м а з а м к н у т а я и к о н с е р в а т и в н а я.

В последнем уравнении под кинетической энергией системы следует понимать сумму энергий поступательного и вращательного движений всех тел системы.