
- •Закон инерции (I закон Ньютона)
- •Механический принцип относительности
- •V0t X'(*)
- •Классический закон сложения скоростей
- •Третий закон Ньютона
- •Третий Закон Ньютона
- •Основой закон динамики (II закон Ньютона)
- •Основной Закон динамики
- •1.2.4 Разные формулировки основного закона динамики
- •Импульс тела
- •Импульс силы
- •Момент импульса тела
- •Импульс момента силы
- •Кинетическая энергия поступательного движения
- •Работа силы
- •Кинетическая энергия вращательного движения
- •Работа момента силы
- •Разные формулировки основного закона динамики приведены в таблице:
- •1.2.5 Особенности работы потенциальных сил. Потенциальная энергия взаимодействия тел
- •Работа потенциальных сил
- •Вычисление потенциальной энергии в разных случаях
- •Глава 1.3 описание движения системы
- •1.3.1 Величины, характеризующие механическое
Разные формулировки основного закона динамики приведены в таблице:
-
Поступательное движение
Вращательное движение


1.2.5 Особенности работы потенциальных сил. Потенциальная энергия взаимодействия тел
При рассмотрении классификации сил мы выделили особый класс сил - потенциальные силы. Основным признаком этого класса сил является то, что они однозначно определяются взаимным расположением взаимодействующих тел и не зависят от скоростей их движения. Среди механических сил к потенциальным относятся гравитационные, в том числе сила тяжести, и упругие, подчиняющиеся закону Гука.
Р
ПРИМЕР
1.
Т
Рис.
33 1m C h1 -dh h2 2












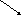




![]()
![]()
![]()
![]() из точки 1, находящейся на высоте
из точки 1, находящейся на высоте![]() над поверхностью земли, перемещается
в точку 2, находящуюся на высоте
над поверхностью земли, перемещается
в точку 2, находящуюся на высоте![]() .
На тело действует сила тяжести. Для
вычисления работы этой силы воспользуемся
определением
.
На тело действует сила тяжести. Для
вычисления работы этой силы воспользуемся
определением ,
где
,
где
![]() ;
;
![]() - проекция силы тяжести на направление
перемещения
- проекция силы тяжести на направление
перемещения .
.
Из
рис. 33 видно, что
![]() ,
знак минус указывает, что при перемещении
тела на
,
знак минус указывает, что при перемещении
тела на![]() в
заданном направлении его высота над
поверхностью Земли убывает на dh:
в
заданном направлении его высота над
поверхностью Земли убывает на dh:
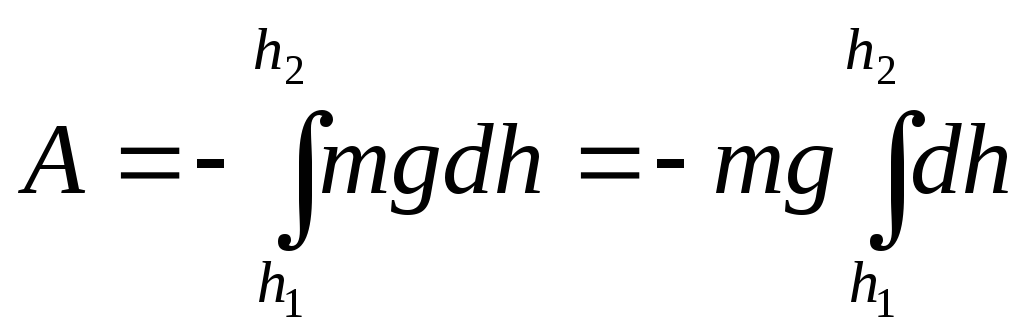 ,
,
![]() .
(л)
.
(л)
О
ПРИМЕР
2.
Т 1 m 

![]()
![]()

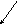





![]()
![]()
М 2

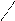

![]()
![]() на основании закона Всемирного
тяготения;
на основании закона Всемирного
тяготения;![]() -
проекция этой силы на направление
перемещения
-
проекция этой силы на направление
перемещения![]() .
.
![]() .
.
Замечаем,
что
![]() .
Если
.
Если![]() ,
то при движении тела происходит
уменьшение расстояния между телами.
,
то при движении тела происходит
уменьшение расстояния между телами.
Рис.
34

или
 .
(лл)
.
(лл)
Так же, как в примере 1, работа гравитационных сил оказалась не зависящей от S, то есть от реальной траектории перемещения, она определяется только положением начальной и конечной точек перемещения (r1 и r2).
Т
ПРИМЕР
3.
Рис.
35











 ,
,
г де
де![]() - на основании закона Гука;
- на основании закона Гука;











![]() -перемещение
тела одновременно является изменением
деформации пружины.
-перемещение
тела одновременно является изменением
деформации пружины.
х
![]() ,
но
,
но
![]() ,
поэтому
,
поэтому![]() ,
,
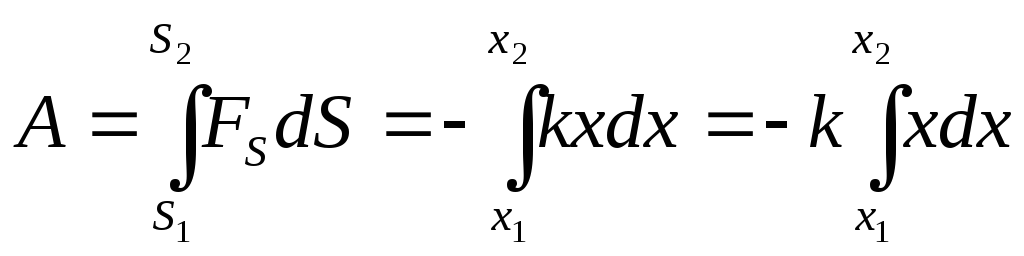
или
![]()
 .
(ллл)
.
(ллл)
Работа силы упругости определяется величиной абсолютной деформации в начальном и конечном состояниях.
И
Работа потенциальных сил
![]()
Из выражений (л), (лл) и (ллл) следует еще одна особенность этих сил, а именно: работа потенциальных сил, при перемещении тела по замкнутой траектории равна нулю, так как при этом h1.=h2, r1=r2 и x1 =x2. Наконец, из сравнения уравнений видно, что все они имеют конструкцию вида:
![]() ,
(о)
,
(о)
где
![]() -некоторая
функция, характеризующая состояние
взаимодействующих тел в данный момент
времени, однозначно определяемая
взаимным расположением тел и зависящая
от физической природы взаимодействия.
Ее принято называтьпотенциальной
энергией взаимодействия
тел.
-некоторая
функция, характеризующая состояние
взаимодействующих тел в данный момент
времени, однозначно определяемая
взаимным расположением тел и зависящая
от физической природы взаимодействия.
Ее принято называтьпотенциальной
энергией взаимодействия
тел.
Уравнение (о) выражает еще одну особенность потенциальных сил: работа потенциальных сил равна убыли потенциальной энергии системы взаимодействующих тел.
Потенциальная энергия зависит от физической природы сил взаимодействия. Сравнивая (о) последовательно с каждым из уравнений (л), (лл) и (ллл) получаем способ вычисления потенциальной энергии в частных случаях:
