механика.физика / стр.87-99

99

2.2. Методика решения типовых задач

Решение задач в курсе физики преследует цель выработать у студентов умение составлять математическую модель явления, описанного в тексте задачи. Основная ценность решения заключается не в получении числовых значений тех или иных величин, а в правильном выборе законов, пригодных для описания рассматриваемого в задаче явления, и в умении применять выбранный закон к конкретной ситуации.

Количество задач, предлагаемых для самостоятельного решения в течение семестра не велико, но каждая задача должна быть разобрана и проанализирована студентом с максимальной полнотой и тщательностью. Решение любой задачи должно начинаться с указания выбранного закона или определения физической величины.

ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РЕШЕНИЯ

1. Решение задач выполняется в отдельной тонкой тетради.

2. Текст задачи записывается полностью, а затем дается краткая

запись условия.

3. По возможности условие и решение иллюстрируется рисунком,

схемой или графиком.

4. Написанию любой формулы должны предшествовать словесные пояснения (указания на используемые законы, определения, геометрические соотношения, математические преобразования или специальные условия, оговоренные в тексте задачи).

5. К каждой формуле должна быть расшифровка всех буквенных обозначений, используемых в ней.

6. После анализа задачи должна быть дана ее математическая модель, то есть система уравнений, описывающая рассматриваемое явление с учетом специфических особенностей, указанных в условии.

7. Решение задачи в большинстве случаев проводится в общем виде.

8. Выражение, полученное для расчета искомой величины, необходимо проверить по размерности.

9. Перед вычислениями все величины переводятся в одну систему единиц и представляются в стандартном виде.

10. Полученный результат необходимо проанализировать и оценить его правдоподобность.

2.2.1. Кинематика поступательного и вращательного движения

Можно выделить два типа кинематических задач.

I тип: По известному закону пути (или угла поворота) найти законы изменения с течением времени других кинематических характеристик и их значения в заданный момент времени.

II тип: По известному закону ускорения (линейного или углового) найти законы изменения с течением времени других кинематических характеристик и их значения в заданный момент времени.

Задачи I типа решаются на основе определений кинематических характеристик

и т.п.

Математическая модель задачи должна содержать как минимум три уравнения: закон пути, закон скорости и закон ускорения для рассматриваемого вида движения.

Задачи II типа решаются на основе кинематических законов:

;

.

Математическая модель задачи, как и в первом случае, содержит не менее трех уравнений: закон ускорения, закон скорости и закон пути.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

З а д а ч а 1. Материальная точка движется прямолинейно так, что закон пути имеет вид , где А = 6 м, В = 3 м/с, С = 2 м/с², .

Построить графики зависимости пути, скорости и ускорения от времени, найти средние значения скорости и ускорения за первые 4 с движения.

А н а л и з (Ч. 1). Задача относится к первому типу, будем решать ее на основе определений скорости и ускорения.

Из заданного по условию закона пути следует, что при

, , то есть движение началось из точки, отстоящей от начала отсчета на м.

Закон скорости найдем как первую производную от закона пути по времени:

.

Из этого уравнения видно, что при, , то есть сначала тело движется в отрицательном направлении по траектории, приближаясь к началу отсчета. При , значит направление скорости меняется при , в этот момент времени , а поскольку V - это производная от пути по времени, то S при принимает экстремальное (минимальное) значение.

Поскольку движение прямолинейное, полное ускорение совпадает со своей тангенциальной составляющей и находится как первая производная от скорости по времени

.

Как видно, ускорение не зависит от времени, следовательно, движение равнопеременное. Знак ускорения во время всего движения положителен, однако до знаки ускорения и скорости разные, значит, движение замедленное, а при знаки ускорения и скорости совпадают - движение ускоренное.

Р

• закон пути

• закон скорости

• закон ускорения.

е ш е н и е (ч.1). Математическая модель задачи:

Для построения графиков составим таблицы значений соответствующих величин, причем график V=V(t) - прямая, поэтому для ее построения достаточно двух точек, а для построения графика S=S(t) необходимо не менее 5 точек и, как было видно из анализа, особой точкой является

V,

.

,

t	0	0,75
V	-3	0

А н а л и з (ч. 2). Для нахождения средних значений скорости и ускорения воспользуемся их определениями:

,

где - пройденное расстояние;

- промежуток времени (по условию 0…4 с, то есть = 4 с).

,

где - скорость в момент времени t = 4 c;

- скорость в момент времени t = 0.

Воспользовавшись результатами анализа I-й части задачи, изобразим на траектории характерные точки движения.

4,87

О

В

А

С

S₀=6

О - начало отсчета;

А - точка, из которой началось движение (при t = 0, S_t = 6);

В - точка изменения направления движения.

Это изменение произошло при с и - отсчитывается не от точки А, а от начала отсчета.

С- точка, в которой тело было через 4 с.

(м).

Р е ш е н и е (ч.2). Пройденное за 4 с расстояние, очевидно, складывается из длин отрезков траектории:

;

(м);

(м);

(м);

(м/с);

; ;

(м/с²).

А н а л и з п о л у ч е н н ы х р е з у л ь т а т о в

1. Закон движения задает положение тела на траектории по отношению к началу отсчета, а не пройденный путь.

2. В интервале 0…1,5 с уравнение имеет два решения, что соответствует тому, что в каждой точке тело побывало дважды, двигаясь сначала в одном, а затем в другом направлении (см. таблицу и график ).

3. Закон скорости является единым на всем протяжении движения (см. график ), но характер движения меняется в зависимости от того одинаковые или разные знаки имеют скорость и ускорение (в первом случае движение ускоренное, во втором - замедленное).

4. В общем случае средние значения скорости и ускорения не могут быть посчитаны как средние арифметические их начального и конечного значений .

5. Поскольку ускорение в данной задаче постоянно, то естественно, что его среднее значение совпало с мгновенным в любой момент времени.

З а д а ч а 2. Вентилятор вращается со скоростью, соответствующей частоте 900 об/мин. После выключения, вращаясь равно-замедленно, он сделал 75 оборотов до остановки. Сколько времени прошло с момента выключения вентилятора до полной его остановки?

А н а л и з. Характер движения известен по условию задачи - равнозамедленное, это значит, что угловое ускорение и знаки угловой скорости и углового ускорения разные. Задача относится ко II типу и решается на основе кинематических законов:

(1)

(2)

Учитывая, что и из (1)

,

подставим найденный закон изменения угловой скорости с течением времени в (2):

Р

- закон углового ускорения

е ш е н и е. Математическая модель задачи:

- закон угловой скорости (3)

- закон для угла поворота, (4)

где

Так как нас интересует время до остановки, то положим в (3) , тогда

,

подставим это значение в (4):

,

откуда

(5)

По условию задана частота вращения об/мин = 15 об/с. Учитывая, что каждому обороту соответствует угол поворота, равный рад., запишем значение угловой скорости:

.

Аналогично связано с числом оборотов :

Подставляя числовые данные в (5), получим:

.

А н а л и з п о л у ч е н н ы х р е з у л ь т а т о в

1. Для равнопеременного движения характерен линейный закон изменения скорости с течением времени и квадратичный закон для перемещения (угла поворота).

2. Графики законов , и для данной задачи имеют вид:

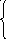
График для угла поворота построен с учетом геометрического смысла производной, как тангенса угла наклона между касательной к графику функции и осью абсцисс. По отношению к углу поворота угловая скорость является производной, а так как с течением времени эта скорость убывает, то на графике углы .

3. Необходимо обратить особое внимание на то, что при получении кинематических законов для конкретного вида движения из общих формулировок (1) и (2) под интеграл подставляются не числовые значения скоростей и ускорений, а законы изменения этих величин с течением времени.

2.2.2. Динамика поступательного и вращательного движений

Законы Ньютона справедливы только в инерциальных системах отсчета. В большинстве задач Землю можно считать инерциальной системой (пренебрегая ее ускорением относительно системы неподвижных звезд), если система не имеет ускорения относительно Земли, ее также можно считать инерциальной. В инерциальных системах отсчета термин "сила" используется для характеристики в з а и м о д е й с т в и я т е л. Изображая силы, действующие на тело, необходимо контролировать "реальность" этих сил, указывая со стороны какого другого тела действует та или иная сила и какова ее природа (тяготение, трение, упругость). Во избежание ошибок не рекомендуется пользоваться терминами типа "скатывающая сила" (это не особая сила, а лишь проекция силы тяжести), " центростремительная сила" (это тоже не особая сила, а сумма проекций сил на нормаль к траектории), "центробежная сила", "сила инерции" и пр.

Основной закон динамики имеет несколько формулировок (в терминах "ускорение-сила", "количество движения - импульс силы", "кинетическая энергия - работа"). Здесь будет рассматриваться применение только первой формулировки: ускорения, приобретаемые телами, прямо пропорциональны интенсивности внешних воздействий и обратно пропорциональны собственным инертным свойствам тел. Поскольку величины, характеризующие интенсивность взаимодействия и собственные инертные свойства тел различны для поступательного и вращательного движений, математическая запись этого закона будет иметь вид

- для поступательного движения

и

- для вращательного движения.

При решении задач удобнее писать так:

и .

ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ

1. Изобразить на чертеже в с е силы, действующие на каждое тело. Проверить реальность сил, указав для каждой силы ее характер (сила упругости, сила трения, сила тяготения).

2. Выбрать координатные оси в соответствии с условиями задачи. Спроектировать все силы на выбранные оси. Указать на чертеже направления скоростей и ускорений всех тел.

3. Записать основное уравнение динамики (II закон Ньютона) в проекциях на выбранные координатные оси для каждого тела и для каждого вида движения в отдельности

.

таких систем уравнения должно быть столько, сколько тел участвует в движении по условию задачи.

4. Проверить полноту системы и при необходимости записать дополнительные условия, выражающие:

а) кинематические связи в соответствии с условием задачи;

б) III закон Ньютона для взаимодействующих тел;

в) особые свойства сил, указанных в задаче в соответствии с законами п.3.

5. Решить полученную систему относительно неизвестной величины в общем виде и результат проверить по размерности.

6. Проанализировать полученный результат.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

З а д а ч а 1. В движущемся лифте на пружинных весах висит груз массой 1 кг. Показания весов Н. Найти ускорение лифта.

А

x

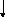
н а л и з. На груз действуют две силы - со стороны Земли сила тяжести и сила упругости со стороны пружины, причем по условию , следовательно, ускорение груза направлено вверх. Силы направлены по одной прямой, поэтому достаточно рассмотреть их в проекции на одну ось, направив ее вертикально вверх.

Спроектируем силы и ускорение на это направление. Запишем второй закон Ньютона в проекции на эту ось:

.

Р е ш е н и е.

; .

Математическая модель задачи:

, (1)

откуда

,

.

А н а л и з п о л у ч е н н ы х р е з у л ь т а т о в

1. При неподвижном лифте и из (1) следует, что .

2. Когда лифт начинает двигаться, груз еще неподвижен, поэтому расстояние между потолком лифта и грузом меняется, пружина дополнительно растягивается или сжимается и .

3. При установившемся движении ускорение груза и лифта совпадают, поэтому ускорение груза, найденное в задаче, одновременно является и ускорением лифта.

4. Важно понимать, что II закон Ньютона определяет направление ускорения тела, а не его скорости. В рассмотренной задаче ускорение направлено вверх, но направление движения лифта однозначно указать нельзя. Лифт может двигаться как вверх (тогда его движение будет ускоренным), так и вниз (тогда его движение будет замедленным).

5. Выразим из (1) , то есть показания весов:

.

Сравним показания весов с силой тяжести в разных ситуациях:

а) - лифт неподвижен или движется равномерно, тогда ;

б) - лифт движется ускоренно вверх или замедленно вниз, тогда ;

в) лифт движется замедленно вверх или ускоренно вниз, тогда ;

г) - лифт свободно падает (пружина не растянута, такую ситуацию называют невесомость).

З а д а ч а 2. Через неподвижный блок массой 1 кг перекинута невесомая нерастяжимая нить, к концам которой привязаны грузы кг и кг. Найти силу давления блока на ось. Трением пренебречь. Блок считать однородным диском. Нить не проскальзывает по блоку.

А н а л и з. В движении участвуют три тела. Рассмотрим силы, действующие на каждое из них. На грузы действуют силы со стороны Земли и и со стороны нити и . Если нить не проскальзывает по блоку, то можно считать, что вращение блока вызывается действием сил натяжения нити и , причем во всех точках слева от блока натяжение нити можно