3

Тангенциальное ускорение

.Тангенциальное ускорение– векторная физическая величина, характеризующая изменение скорости тела по абсолютному значению, численно равная первой производной от модуля скорости по времени и направленная по касательной к траектории в ту же сторону, что и скорость, если скорость возрастает, и противоположно скорости, если она убывает.

4

Нормальное ускорение

.Нормальное ускорение– векторная физическая величина, характеризующая изменение направления скорости, численно равная отношению квадрата скорости к радиусу кривизны траектории, направленная вдоль радиуса кривизны к центру кривизны:

Рис. 1.17

.

Т

ак как векторыинаправлены под прямым углом, то (рис. 1. 17)

, (1.2.9)

5.Угловое ускорение– векторная физическая величина, характеризующая изменение угловой скорости, численно равная первой производной угловой скорости по времени и направленная вдоль оси вращения в ту же сторону, что и угловая скорость, если скорость возрастает, и противоположно ей, если она убывает.

Формулу вставить (1.2.10)

СИ:

Полное ускорение

(линейное)

Поскольку мы ограничиваемся рассмотрением вращения вокруг неподвижной оси, угловое ускорение не делится на составляющие подобно линейному.

Угловое ускорение

Связь между угловыми характеристиками

вращающегося тела и линейными

характеристиками движения его отдельных точек

Р

СИ:

ассмотрим одну из точек вращающегося тела, которая находится от оси вращения на расстоянииR, то есть движется по окружности радиуса R (рис. 1.18).

Рис. 1.18

R

По истечении времениточка А переместится в положение А₁, пройдя расстояние , радиус-вектор повернется на угол. Центральный угол, опирающийся на дугу, в радианной мере равен отношению длины дуги к радиусу кривизны этой дуги:

A

A^э



О

|S|

.

Это остается справедливым и для бесконечно малого интервала времени:. Далее, используя определения, легко получить:

; (1.2.11)

Связь между линейными и угловыми характеристиками

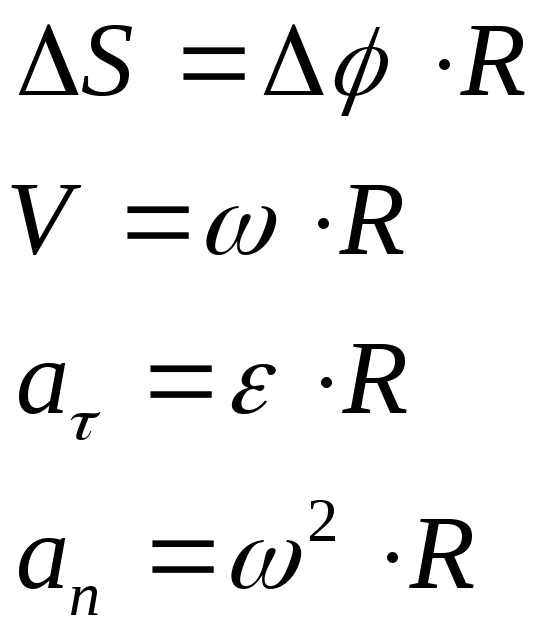
; (1.2.12)

. (1.2.13)

1.1.2. Классификация движений. Кинематические законы

Кинематическими законами будем называть законы, выражающие изменение кинематических характеристик движения с течением времени:

- закон пути или;

- закон скорости или;

- закон ускорения или.

Н

Ускорение

Ускорение гоночного автомобиля на старте 4-5 м/с²

Ускорение реактивного самолета при посадке

6-8 м/c²

Ускорение свободного падения вблизи поверхности Солнца 274 м/c²

Ускорение снаряда в стволе орудия 10⁵ м/c²

аиболее информативной характеристикой движения является ускорение, поэтому оно используется в качестве основания для классификации движений.

Нормальное ускорение несет информацию об изменении направления скорости, то есть об особенностях траектории движения:

- движение прямолинейное (направление скорости не меняется);

- движение криволинейное.

Тангенциальное ускорение определяет характер изменения модуля скорости с течением времени. По этому признаку принято выделять следующие виды движения:

- равномерное движение (абсолютное значение скорости не меняется);

- ускоренное движение

- неравномер- (скорость возрастает)

ное движе- -замедленное движе

ние ние (скорость убывает).

Наиболее простыми частными случаями неравномерного движения являются движения, при которых

- тангенциальное ускорение не зависит от времени, остается постоянным во время движения – равнопеременное движение (равноускоренное или равнозамедленное);

или- тангенциальное ускорение меняется с течением времени по закону синуса или косинуса – гармоническое колебательное движение (например, грузик на пружине).

Аналогично для вращательного движения:

- равномерное вращение;

- неравномерное вращение

Типы движения записать более компактно

-равноускоренное

вращение

- замедлен-

ное вращение;

- равнопе-

ременное вращение

Крутильные колебания (например, трифилярный подвес – диск, подвешенный на трех упругих нитях, и совершающий колебания в горизонтальной плоскости).

1

-1

Если известен один из кинематических законов в аналитической форме, то можно найти другие, при этом возможны два типа задач:

I тип – по заданному закону пути илинайти закон скоростиилии закон ускоренияили;

II тип – по заданному закону ускорения илинайти закон скоростиилии закон путиили.

Эти задачи являются взаимно обратными и решаются на основе применения обратных математических операций. Первый тип задач решается на основе определений, то есть путем применения операции дифференцирования.

ПРИМЕР.

- задано

- ?

- ?.

Второй тип задач решается путем интегрирования. Если скорость есть первая производная от пути по времени, то путь по отношению к скорости можно найти как первообразную. Аналогично: ускорение есть производная от скорости по времени, тогда скорость по отношению к ускорению – первообразная. Математически эти действия выглядят так:

- приращение пути за бесконечно малый промежуток времени . Для конечного интервала отдоинтегрируем:. По правилам интегрирования. Чтобы взять интеграл в правой части, нужно знать вид закона скорости, то есть. Окончательно, для нахождения положения тела на траектории в произвольный момент времени получаем:

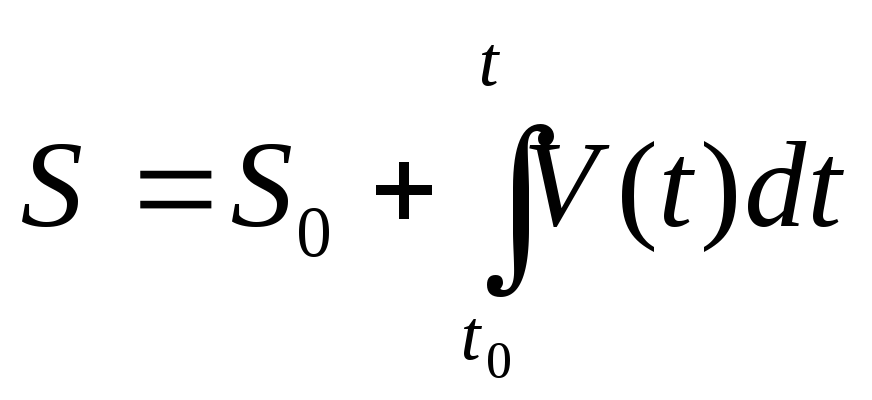, где (1.2.14)

- изменение скорости за бесконечно малый промежуток времени .

Для конечного интервала от до: