86

Кадры самоконтроля к теме "Кинематические характеристики поступательного и вращательного движений"

1. Угловая скорость действительно направлена вдоль оси вращения, но ее направление Вы указали неверно (cм. определение и рис. 13 в информационной части).

1-2 Обратите внимание: в с е в е к т о р н ы е х а р а к т е р и с т и к и в р а щ а т е л ь н о г о д в и ж е н и я н а п р а в л е н ы в д о л ь о с и в р а щ е н и я!

3. Направление вращения тела и направление угловой скорости связаны правилом правого винта - верно.

3. Еще раз вернитесь к информационной части (рис. 13).

3. Линейная скорость всегда направлена по касательной к траектории.

3. Движение, действительно равномерное так как , но для прямолинейного движения необходимо.

3. Прежде чем отвечать на вопрос, необходимо уточнить определения - только тогда работа с тренажером будет эффективной (см. разд. 1.3 информационной части).

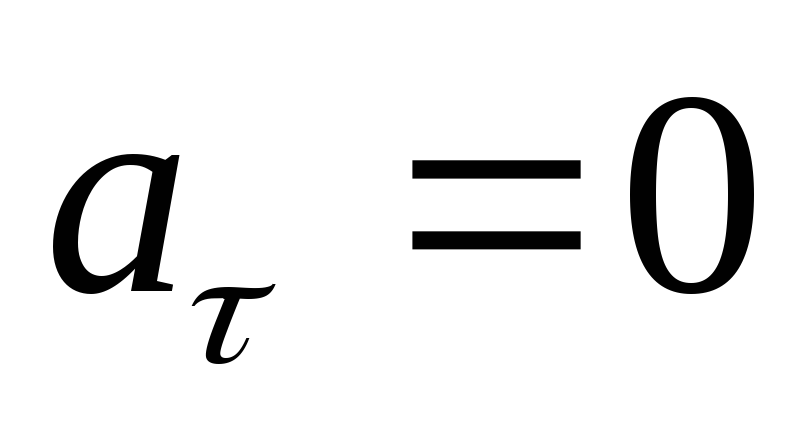3. - это признак равномерного движения, при котором скорость остается постоянной по модулю. По определению , и если учесть, чтоV=const и по условию , то иR= const, значит тело движется по криволинейной траектории с постоянным радиусом кривизны, то есть по окружности. Ваш ответ верен.

3. Действительно, так как -движение равномерное, а- движение криволинейное. Но вы не до конца проанализировали условие: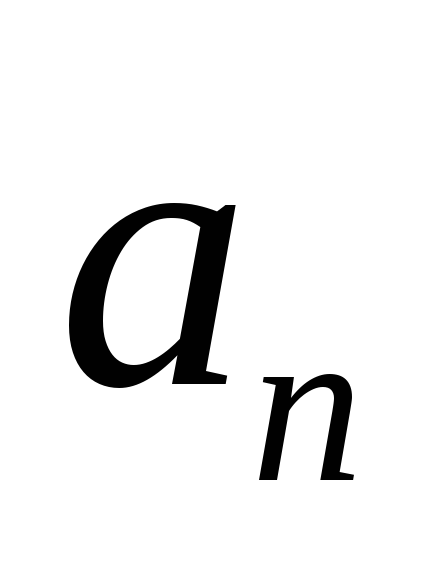- не просто отлично от нуля, но и остается постоянным. По определению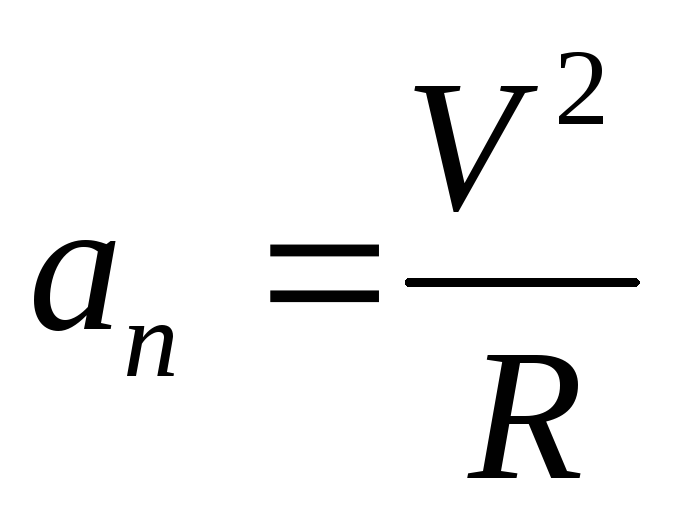. Какие дополнительные выводы относительноV и R вы можете сделать?

3. Полное ускорение складывается из нормальной и тангенциальной составляющих (см. рис. 17) и в общем случае может быть направлено под произвольным углом к скорости. Известно также, что векторперпендикулярен вектору. Полное ускорение может совпадать с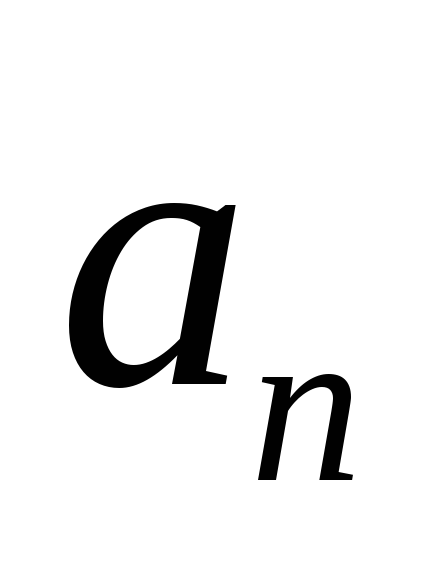в том случае, когда. Для какого движения это справедливо?

3. Из предложенных вариантов вы выбрали верный ответ, но он не является единственным. Движение действительно должно быть равномерным, так как угол между скоростью и ускорением равен 90⁰ только в том случае, когда полное ускорение совпадает с нормальным, а , но форма траектории не обязательно должна быть окружность.

Для лучшего понимания попытайтесь ответить на вопрос этого задания, если угол между векторами скорости и ускорением . Для каждой ситуации сделайте рисунок.

3. Обратите внимание: , но модули этих векторов не связаны аналогичным соотношением,, потому что эти векторы не направлены по одной прямой (см. рис. 17).

3. Такой ответ был бы возможен, если бы векторы 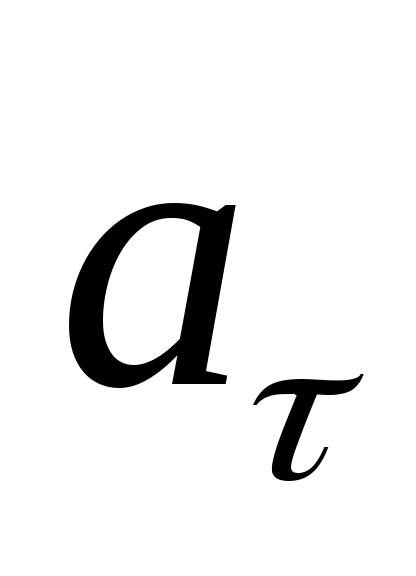ибыли направлены по одной прямой в противоположные стороны, но это не так (см. рис. 17).

1-14 В соответствии с рис. 17 модули векторов связаны соотношением .

1-15 См. кадр 1-14.

1-16 Если угол между скоростью и ускорением меньше , то движение ускоренное, и тангенциальное ускорение совпадает по направлению со скоростью. А между тангенциальным и нормальным ускорениями угол всегда равен. Сделайте рисунок и тогда ответ будет очевиден.

17. Верно.

1-18 ? - такое возможно, если угол между скоростью и ускорением 45⁰, но это не соответствует условию.

1-19 Уточните определения sin , cos  и будьте внимательны.

20. Направление вращения и угловая скорость связаны правилом правого винта (то есть направлено по оси вращения влево), а поскольку по условию движение замедленное, то скорость и ускорение имеют противоположные направления. Вариант А правильный.

1-21 Направление вращения не связано непосредственно с угловым ускорением. Сначала надо определить направление угловой скорости, а далее обратить внимание на характер движения (ускоренный или замедленный).

22. В общем случае , но по условию движение равномерное, значити, откуда следует, что приV=const связь между ускорением и радиусом кривизны траектории обратная. Радиус кривизны увеличивается по условию, значит, ускорение уменьшается.

22. Проверьте в кадре 1-22, где вы допустили ошибку в рассуждениях.

22. С радиусом кривизны связано нормальное ускорение (). По условиюV=const, а R изменяется, следовательно, нормальное ускорение не может оставаться неизменным. А что вы можете сказать об ? Обдумайте ответ еще раз.

22. Вы проанализировали ситуацию правильно.

22. Это задание, как и предыдущее основано на анализе формулы , но теперьR=const (движение - по окружности). Внимательно прочтите условие - что известно об изменении V?

1-27 По условию движение равнозамедленное, что означает , поэтому полное ускорение ведет себя так же, как нормальное.

28. Без рисунка вы не сможете дать правильный ответ.

1-29 На вашем рисунке ? ?направлено противоположно скорости? Если на все эти вопросы вы даете положительный ответ, то сомнений в правильности варианта В) не остается.

30. По определению , то есть пропорциональноквадрату скорости. Если V увеличивается в 2 раза, то числитель этой дроби увеличивается не в два раза!

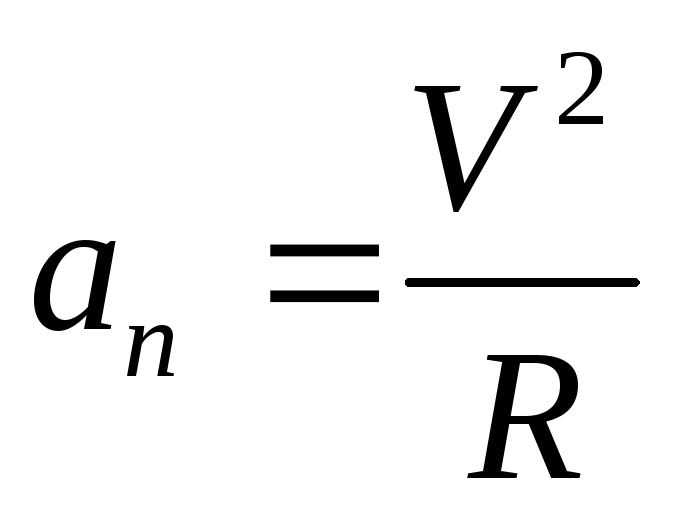
30. По определению  увеличение V и уменьшение R приводят к возрастанию 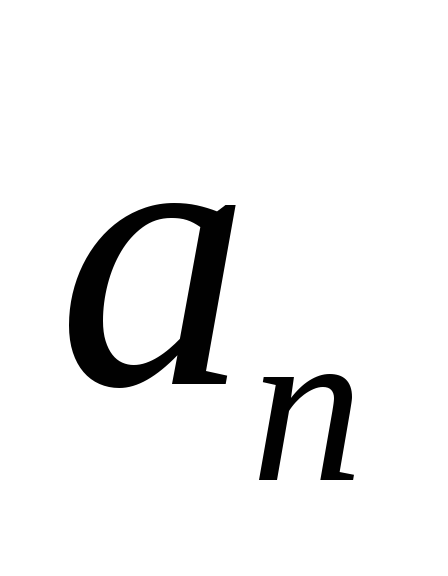, но по условиюостается постоянным.

30. С анализом функциональных зависимостей вы справились хорошо. При выполнении следующего задания эти зависимости надо представить в графической форме. Будьте внимательны.

30. Поскольку - движение ускоренное, скорость растет, а вместе с ней растет и нормальное ускорение (приR=const), но растет не так, как вы подумали. Представьте сначала на графике закон изменения скорости точки с учетом, что .

30. При и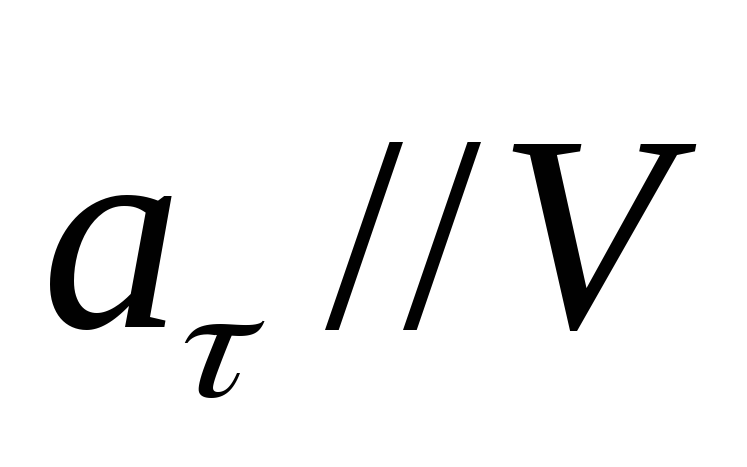- скорость точки растет с течением времени п о л и н е й н о м у закону, так как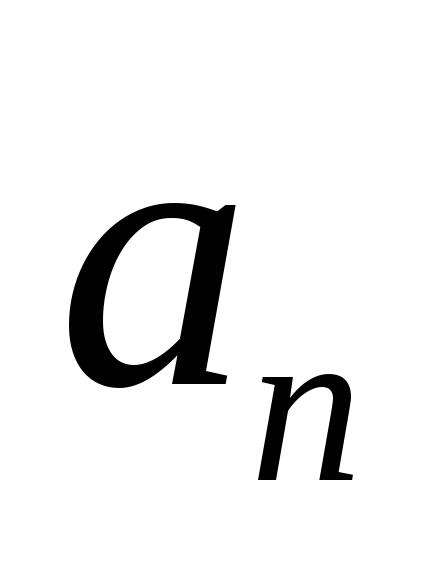~(приR=const), то 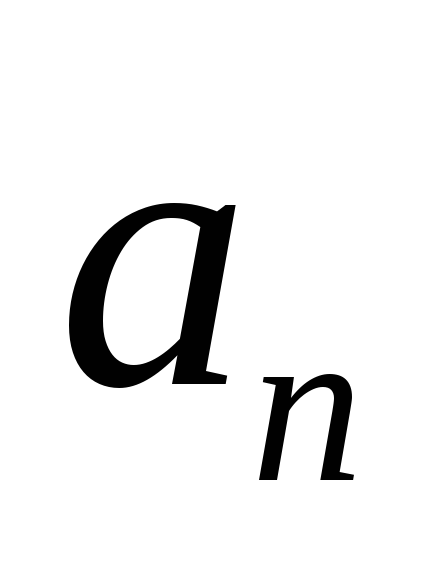с течением времени должно расти по квадратичному закону, как это изображено в данном варианте.

30. По определению . По условиюR=const (движение по окружности), но поскольку - скорость точки меняется с течением времени, значит должно меняться и.

30. Задания 13, 14, 15 посвящены анализу связи между угловыми и линейными характеристиками. Рассмотрим соотношение , из которого следует, что если для двух точек, тоV больше там, где больше R, но если V=const, то () больше там, где меньше R.

Поэтому сначала нужно найти такую характеристику, которая остается постоянной для двух рассматриваемых точек.

Обратите внимание: если две точки принадлежат о д н о м у и тому же в р а щ а ю щ е м у с я т е л у, то все у г л о в ы е характеристики движения для них о д и н а к о в ы.

Если же точки принадлежат телу, движущемуся п о с т у п а т е л ь н о, то о д и н а к о в ы м и должны быть л и н е й н ы е характеристики, так как в противном случае тело будет деформироваться в процессе движения. Так, в задании 13 точки А и В не могут иметь разные скорости, иначе лента, связывающая шкивы, разорвется. Но и тогда правильный ответ очевиден.

30. Рукоятка и ворот вращаются как одно целое, причем радиус окружности, по которой движется точка 1, больше, чем для точки 2. Далее, используя то, что было сказано в кадре 1-36, Вы легко найдете правильный ответ.

30. Радиусы окружностей, по которым движутся точки А и В о д н о г о тела, разные, поэтому одновременное равенство их угловых и линейных характеристик не возможно.

1-39 Поскольку точки А и В принадлежат одному и тому же вращающемуся телу, варианты ответов Б) и Г) сразу отпадают.

40. Правильно.