
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет № 1 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Телеграфное уравнение.
-
Найти области на плоскости (х,у) в которых уравнение Yuxx+2xuxy+uyy=0 имеет эллиптический тип
-
Найти решение уравнения ut=9uxx для следующего начального распределения температуры

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет № 2 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Типы линейных дифференциальных уравнений в частных производных второго порядка
-
Найти решение волнового уравнения utt=4uxx методом характеристик (методом Даламбера), если u|t=0=x2+x, ut|t=0=1.
-
Привести к каноническому виду уравнение
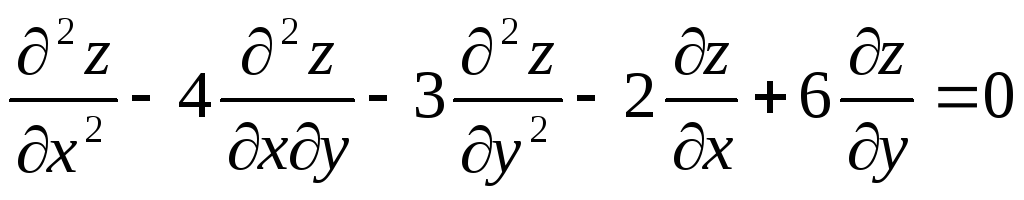
|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №3 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
|
-
Приведение к каноническому виду дифференциального уравнения второго порядка от двух независимых переменных. Понятие характеристик.
-
Определить, является ли функция гармонической

-
Найти решение уравнения ut=uxx , удовлетворяющее начальным условиям

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №4 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Задача о распространении тепла. Уравнение теплопроводности для нестационарного случая
-
Найти форму струны, определяемой уравнением utt=9uxx в момент t=/6, если u|t=0=cos2x, ut|t=0=x+cosx
-
Найти решение уравнения ut=uxx для следующего начального распределения температуры

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №5 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
|
-
Задача о поперечных колебаниях струны. Постановка начально-граничных условий.
-
Найти решение волнового уравнения utt=2uxx методом характеристик (методом Даламбера), если u|t=0=x2, ut|t=0=sinx.
-
Найти решение уравнения ut=4uxx , удовлетворяющее начальным условиям

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №6 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Задача о колебании стержня.
-
Определить, является ли функция гармонической U(x,y)=(x2-y2)(2х+1)
-
Найти решение уравнения теплопроводности, если левый конец х=0 полу бесконечного стержня теплоизолирован, а начальное распределение температуры

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №7 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Задача о колебании мембраны.
-
Найти области на плоскости (х,у) в которых уравнение Yuxx+2xуuxy+хuyy=0 имеет параболический тип
-
Найти решение уравнения теплопроводности ut=uxx, удовлетворяющее начальному условию u(x,t)|t=0=sinx и краевым условиям u|x=0=u|x=l=0
|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №8 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Уравнение неразрывности
-
Найти форму струны, определяемой уравнением utt=4uxx в момент t=/2, если u|t=0=cosx, ut|t=0=sinx
-
Привести к каноническому виду уравнение
|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №9 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Задача обтекания
-
Найти решение волнового уравнения utt=9uxx методом характеристик (методом Даламбера), если u|t=0=sin2x, ut|t=0=x.
-
Найти решение уравнения теплопроводности, если левый конец х=0 полу бесконечного стержня теплоизолирован, а начальное распределение температуры

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №10 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Уравнения акустики
-
Определить, является ли функция гармонической
-
Решение уравнения колебания струны, закрепленной на концах, методом разделения переменных (методом Фурье). Струна, закрепленная на концах х=0 и х=1. Начальные отклонения точек струны равны 0, а начальная скорость выражается формулой

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №11 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
|
-
Уравнение Лапласа. Уравнение теплопроводности для стационарного случая.
-
Определить, является ли функция гармонической
-
Решение уравнения колебания струны, закрепленной на концах, методом разделения переменных (методом Фурье). Струна, закрепленная на концах х=0 и х=1, в начальный момент имеет форму u=2x-1. Найти форму струны для любого момента времени t, если начальные скорости отсутствуют.
|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №12 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Решение задачи Дирихле в круге методом Фурье
-
Решение уравнения колебания струны методом характеристик (методом Даламбера).Найти форму струны, определяемой уравнением utt=uxx в момент t=, если u|t=0=2x-1, ut|t=0=cosx
-
Найти решение уравнения ut=1/4uxx для следующего начального распределения температуры

|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №13 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Решение задачи Коши для уравнения колебания струны методом характеристик. Формула Даламбера.
-
Найти области на плоскости (х,у) в которых уравнение хуuxx+2xuxy+уuyy=0 имеет гиперболический тип
-
Струна, закрепленная на концах х=0 и х=1, в начальный момент имеет форму u=x2+2. Найти форму струны для любого момента времени t, если начальные скорости отсутствуют.
|
Составил доцент Забелина Н.А. 22 октября 2010 ____________________ |
Утверждаю ____________ Зав. кафедрой Свешников И.В. 22 октября 2010 |
|
Министерство образования и науки РФ Читинский государственный университет Кафедра физики и техники связи |
Экзаменационный билет №14 По дисциплине: Методы математической физики Специальность ТКВ, ТКР |
-
Распространение света в плоском волноводе
2. Найти решение волнового уравнения utt=1/4uxx методом характеристик (методом Даламбера), если u|t=0=x2, ut|t=0=sin2x.
