Метод эквивалентных соотношений.

Этот метод применяется в случаях, когда удается обосновать, какому относительному изменению количества продукции эквивалентно, с точки зрения общего эффекта от использования продукции по назначению, рассматриваемое относительное изменение данного показателя качества или на сколько процентов можно, например, уменьшить число единиц продукции, чтобы обеспечить те же потребности при увеличении данного показателя качества на 1%.

В этих случаях коэффициенты весомости для средних взвешенных геометрических показателей качества находят по формуле

Наиболее важен случай, когда одинаковые относительные изменения количества продукции эквивалентны некоторым ее показателям качества. Здесь коэффициенты весомости для всех показателей качества, обладающих указанным свойством, можно принять равными единице.

Пример. Пусть Т—средний ресурс электроламп данного типа, — число, определяемое условием замены вышедших из строя ламп. Увеличение Т на 1 % позволит обеспечить те же потребности при числе ламп, меньшем на 1%. Следовательно, относительное изменение среднего ресурса здесь эквивалентно такому же относительному измене­нию числа электроламп. Коэффициент весомости для ресурса, электроламп при вычислении среднего взвешенного геометрического показателя можно принять равным единице.

Метод стоимостных регрессионных зависимостей.

Этот метод основан на построении приближенных зависимостей между затратами на создание и эксплуатацию продукции данного вида (или пропорциональными им показателями) и показателями качества продукции. Метод целесообразно применять в тех случаях, когда имеющееся число сравниваемых вариантов продукции достаточно велико и превосходит число выбранных показателей.

Вид зависимости, как правило, выбирают соответственно, используемому комплексному показателю качества. Например, для среднего взвешенного геометрического показателя для построения регрессионной зависимости между затратами и показателями качества следует использовать следующее выражение

где S_ср и p_ср - величины, полученные усреднением по всем вариантам продукции фактических затрат ипоказателей качества;

a_i – параметры апроксимации, определяемые методом “наименьших квадратов”.

В этом случае параметры апроксимации являются коэффициентами весомости.

Например, сравнивается N вариантов двигателей. Каждый вариант характеризуется набором из (n+1) показателей качества: p_1k , p_2k , …, p_nk , S_k .

Показатели p_ik при увеличении своего значения характеризуют улучшение качества двигателя (мощность, крутящий момент, КПД, средний ресурс и т.п.); S_k –показатель качества двигателя, уменьшение которого характеризует улучшение качества двигателя (общая масса, затраты на производство и эксплуатацию и т.п.).

Предполагая, что для комплексной оценки уровня качества двигателей будет использоваться средний взвешенный геометрический показатель, построим линейную регрессионную зависимость между логарифмами показателя S_k и логарифмами показателей качества p_1k , p_2k , …, p_nk. Выражение для линейной регрессионной зависимости имеет вид

,

где a_i – коэффициент весомости показателя p_i;

;

;

;

.

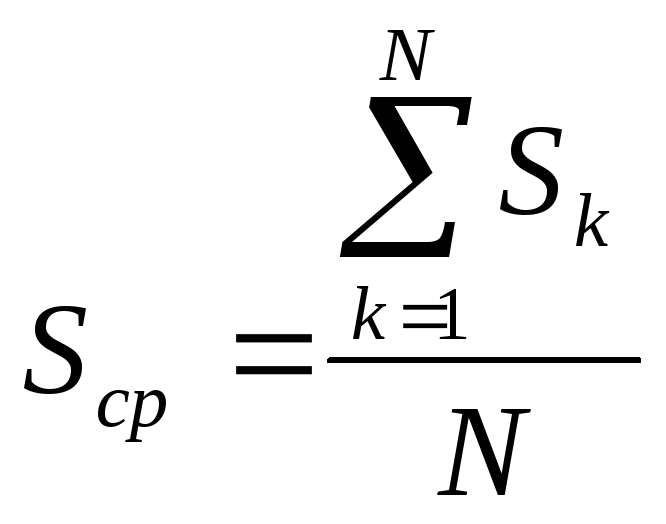Параметры a_i определяются методом наименьших квадратов.