Тема 3. Линейная алгебра
3.1.Теоретические вопросы
1. Определение матрицы. Порядок матрицы.
2. Различные виды матриц.
3. Сложение матриц и умножение матрицы на число.
4. Умножение матриц.
5. Минор и ранг матрицы.
6. Обратная матрица.
7. Системы линейных уравнений в матричной форме.
8. Теорема Кронекера- Капелли.
9. Исследование систем линейных уравнений общего вида.
10. Метод Гаусса.
3.2.Варианты заданий
Задание №1. Выполнить действие с матрицами
Вариант№
1.
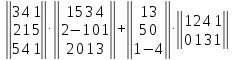
Вариант№
2.
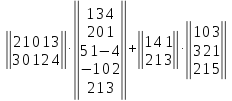
Вариант№
3.
Вариант№
4.
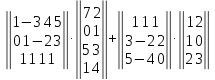
Вариант№
5.
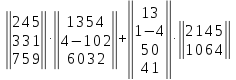
Вариант№
6.
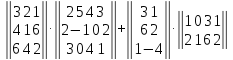
Вариант№
7.
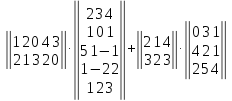
Вариант№
8.
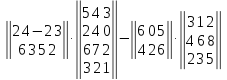
Вариант№
9.
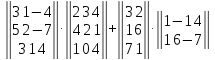
Вариант№
10.
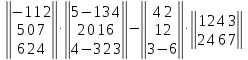
Вариант№
11.
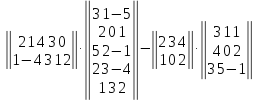
Вариант№
12.
Вариант№
13.
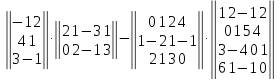
Вариант№
14.
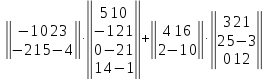
Вариант№
15.
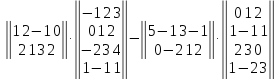
Вариант№
16.
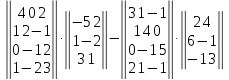
Вариант№
17.
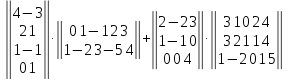
Вариант№
18.
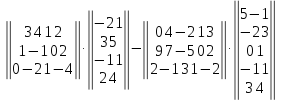
Вариант№
19.
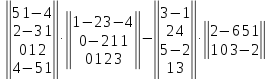
Вариант№
20.
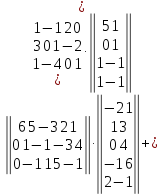
Вариант№
21.
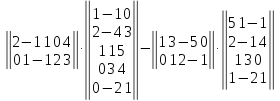
Вариант№
22.
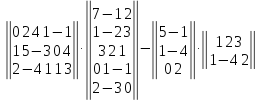
Вариант№
23.
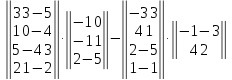
Вариант№
24.
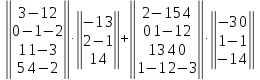
Вариант№
25.
Вариант№
26..
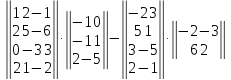
Вариант№
27.
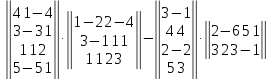
Вариант№
28.
Вариант№
29.
Вариант№
30.
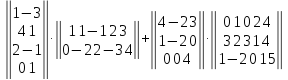
Задание №2. Найти ранг матрицы
Вариант№
1.
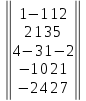Вариант№
2.
Вариант№
3.
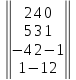
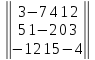Вариант№
4.
Вариант№
5.
Вариант№
6.
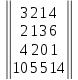
Вариант№
7.
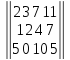Вариант№
8.
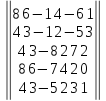
Вариант№
9.
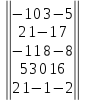Вариант№
10.
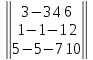
Вариант№
11.
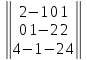Вариант№
12.
Вариант№
13.
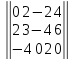Вариант№
14.
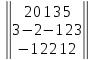
Вариант№
15.
Вариант№
16.
Вариант№
17.
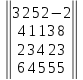Вариант№
18.
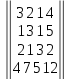
Вариант№
19.
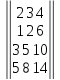Вариант№
20.
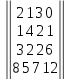
Вариант№
21.
Вариант№
22.
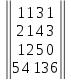
Вариант№
23.
Вариант№
24.
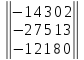
Вариант№
25.
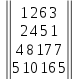Вариант№
26.
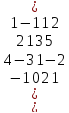
Вариант№
27.
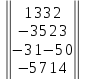Вариант№
28.
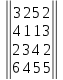
Вариант№
29.
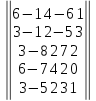Вариант№
30.
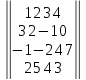
Задание №3. Решить систему уравнений с помощью обратной матрицы
Вариант№1.
Вариант№2.
Вариант№3.
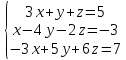Вариант№4.
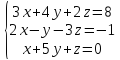
Вариант№5.
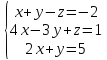Вариант№6.
Вариант№7.
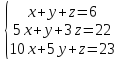Вариант№8.
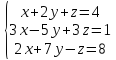
Вариант№9.
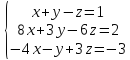Вариант№10.
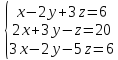
Вариант№11.
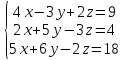Вариант№12.
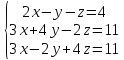
Вариант№13.
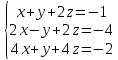Вариант№14.
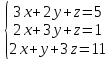
Вариант№15.
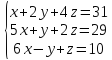Вариант№16.
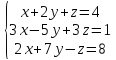
Вариант№17.
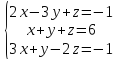Вариант№18.
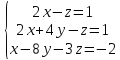
Вариант№19.
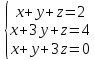Вариант№20.
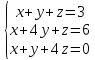
Вариант№21.
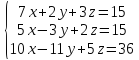Вариант№22.
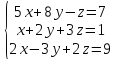
Вариант№23.
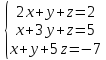Вариант№24.
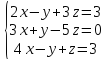
Вариант№25.
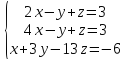Вариант№26.
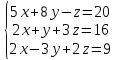
Вариант№27.
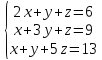Вариант№28.
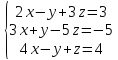
Вариант№29.
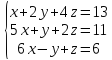Вариант№30.
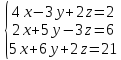
Задание №4. Исследовать систему уравнений на совместность и найти общее решение в случае совместности
Вариант№1.
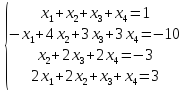
Вариант№2.
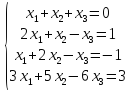
Вариант№3.
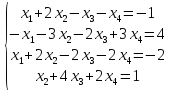
Вариант№4.
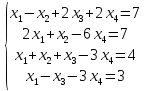
Вариант№5.
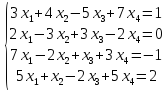
Вариант№6.
Вариант№
7.
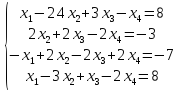
Вариант№
8.
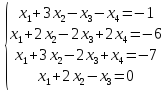
Вариант№
9.
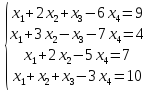
Вариант№10.
Вариант№
11.
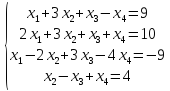
Вариант№
12.
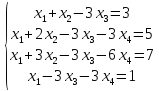
Вариант№
13.
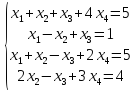
Вариант№
14.
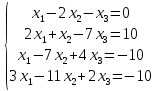
Вариант№
15.
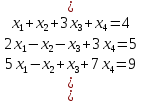
Вариант№
16.
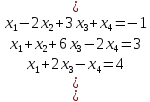
Вариант№
17.
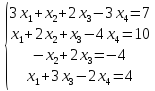
Вариант№
18.
Вариант№
19.
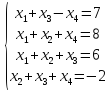
Вариант№
20.
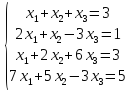
Вариант№
21.
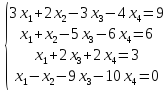
Вариант№
22.
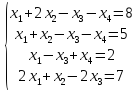
Вариант№
23.
Вариант№
24.
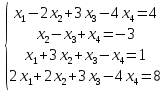
Вариант№
25.
Вариант№
26.
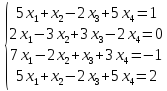
Вариант№
27.
Вариант№
28.
Вариант№
29.
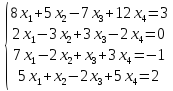
Вариант№
30.
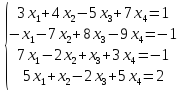
Тема 4. Введение в анализ
4.1. Теоретические вопросы
1. Множество действительных чисел. Модуль действительного числа, свойства модуля.
2. Определение функции одной действительной переменной. Область определения и область изменения функции.
3. Основные элементарные функции их свойства и графики.
4. Определение предела функции в точке и на бесконечности.
5. Числовая последовательность. Предел числовой последовательности.
6. Бесконечно малые функции и их свойства.
7. Бесконечно большие функции и их свойства.
8. Связь бесконечно малых и бесконечно больших функций.
9. Понятие ограниченной функции. Теорема об ограниченности функции, имеющей предел.
10. Теоремы о пределах (правила предельного перехода).
11. Первый замечательный предел.
12. Второй замечательный предел.
13. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
14. Непрерывность функции в точке.
15. Односторонние пределы функции в точке. Достаточное условие непрерывности функции в точке.
16. Точки разрыва функции. Их классификация.
17.Непрерывность элементарных функций.
18. Действия над непрерывными функциями.
19. Непрерывность сложной функции.
20. Свойства функций непрерывных на замкнутом промежутке.