
KURSOVAYa_RABOTA_INFORMATIKA
.doc
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Забайкальский государственный университет»
(ФГБОУ ВПО «ЗабГУ»)
Энергетический факультет
Кафедра информатики, вычислительной техники и прикладной математики
ЗАДАНИЕ
на курсовую работу
по дисциплине «Информационные технологии»
Студенту Огнёву А. А.
Тема работы: Вычисление в MS Excel
Исходные данные к работе
-
Решить систему уравнения двумя способами:
-
методом Крамера
-
с помощью обратной матрицы
-
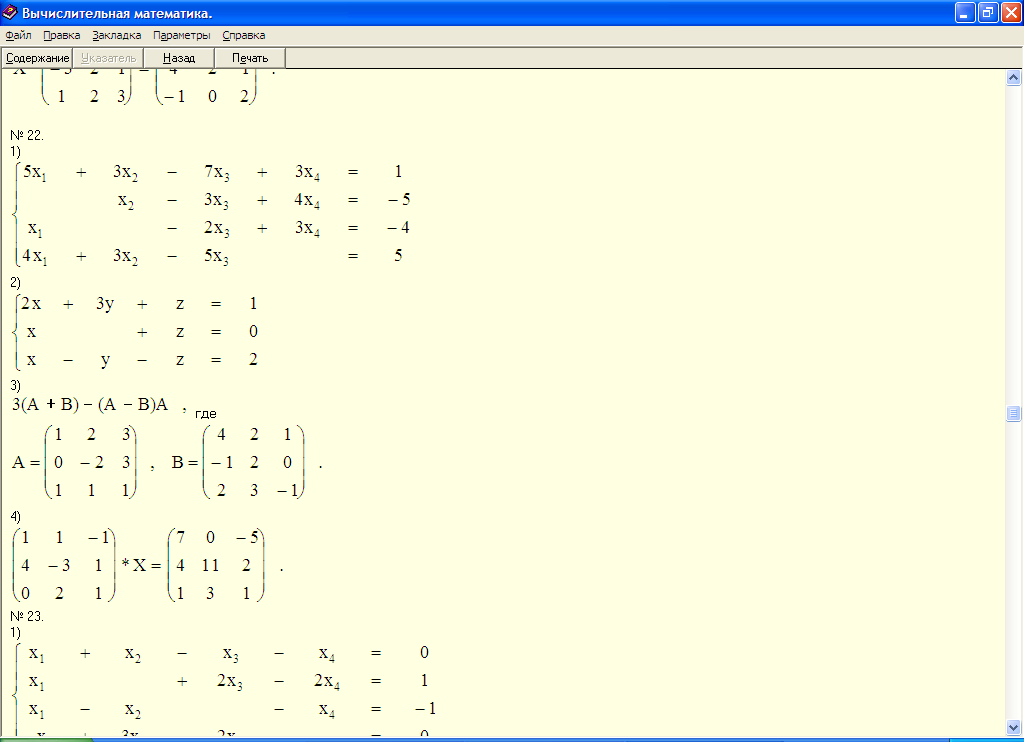
-
Решить уравнения
-
1)arctg(x) +2x-1=0
-
2)3x4+4x3-12x2+1=0
-
Построить на диаграмме функцию, которая является аппроксимацией функции y(x), заданной таблично:
|
X |
-9,78 |
-8,94 |
-8,49
|
-8,20 |
-8,17 |
-7,09 |
-4,62 |
-3,76 |
-3,16 |
-2,48 |
-2,45 |
-1,55 |
-1,47 |
0,25 |
1,88 |
4,18 |
5,92 |
6,51 |
7,54 |
7,96 |
|
Y |
327,96 |
270,45 |
242,07 |
224,81 |
221,22 |
161,91 |
60,77 |
37,66 |
25,65 |
12,89 |
13,75 |
4,07 |
3,26 |
6,70 |
29,74 |
99,77 |
180,58 |
212,15 |
277,22 |
305,74 |
-
Н
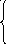 айти
min(max)
значение функции, учитывая ограничения
айти
min(max)
значение функции, учитывая ограничения
6x1-5x217
x1+4x234
-4x1+9x217
f=4x1+3x2
Рекомендуемая литература
-
Гельман В. Я. Решение математических задач средствами
Excel:СПб Питер,2003- 240 стр.
-
Excel: Сборник примеров и задач: Учеб. пособие для вузов.
ФиС,2008- 336 стр
Дата выдачи задания « » 20 г.
Дата представления руководителю « » 20 г.
Руководитель курсовой работы
Реферат
Пояснительная записка – 13 с., 0 рис., 2 табл., 2 источника, 0 прил.
Данная работа предназначена для выполнения заданий с помощью программы MS Excel: решение систем уравнений, уравнений с одной переменной, построение графика, нахождение max(min) значения функции. Программа полностью демонстрирует все возможности данной курсовой работы.
-
Решение систем уравнений двумя способами:
Метод Крамера:
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b.
Для дальнейшего решения необходимо:
-
Вычислить определитель матрицы A.
-
Установим курсор в ячейку I10 и обратимся к мастеру функций.
-
В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций.
-
Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.
-
Для вычисления вспомогательных определителей введем формулы:
-
I11=МОПРЕД(B6:E9),
-
I12=МОПРЕД(B11:E14),
-
I13=МОПРЕД(B16:E19),
-
I14=МОПРЕД(B21:E24).
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 - вспомогательные.
-
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный.
-
В ячейку K11 введём формулу =I11/$I$10.
-
Скопируем её содержимое в ячейки K12, K13 и K14.
-
Система решена.
С помощью обратной матрицы:
Введём матрицу A и вектор b в рабочий лист MS Excel. В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы необходимо вычислить матрицу, обратную к A.
Для дальнейшего решения необходимо:
-
Выделим ячейки для хранения обратной; пусть в нашем случае это будут ячейки B6:E9.
-
Обратимся к мастеру функций
-
В категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы, щелкнув по кнопке OK
-
В диалоговом окне необходимо заполнить поле ввода Массив. Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица - в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
-
Умножаем полученную обратную матрицу на вектор b.
-
Выделим ячейки для хранения результирующего вектора, например H6:H9.
-
Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц.
-
Перейдём ко второму шагу мастера функций.
-
Появившееся диалоговое окно содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b).
-
После заполнения полей ввода нажимаем кнопку OK.
-
В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор х), находится в ячейках H6:H9.
-
Проверяем, правильно ли решена система.
-
Умножаем матрицу A на вектор x и получаем в результате вектор b (умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(В1:Е4;Н6:Н9), так как было описанной выше).
-
Система решена.
-
Решение уравнений:
1) arctg(x) +2x-1=0
2) 3x4+4x3-12x2+1=0
Для решения необходимо:
-
В ячейку А1 заносим ориентировочное значение – х, например 2.
-
В ячейку В1 заносим левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку А1. (Например =atanA1+2*A1-1)
-
Включаем подбор параметра.
-
В поле Установить в ячейке указываем В1, а в поле Значение - 0 (правая часть уравнения), в поле Изменяя значение – А1.
-
Нажимаем кнопку ОК и получаем результат подбора. Сохраняем. Таким образом, в ячейке А1 получаем приближенное значение
х=-2,2518E+14. При этом точность решения – вместо 0 в ячейке В1 получаем 2,2518E+14.
-
Уравнение решено.
-
Построение на диаграмме функцию, которая является аппроксимацией функции y(x), заданной таблично:
Для построения необходимо:
-
Ввести в ячейку А1 – х, затем в ячейки А2:А22 все значения х. Далее в ячейку В1 – у, а затем в ячейки В2:В22 все значения у.
-
Строим диаграмму по введенным данным:
-
На панели инструментов вызываем Мастер диаграмм.
-
Выбираем тип диаграммы Точечный.
-
Нажимаем кнопку Готово. Получаем график.
-
Осуществим аппроксимацию полученной кривой:
-
Указатель мыши устанавливаем на одну из точек графика и щелкаем правой кнопкой
-
В появившемся контекстном меню выбираем пункт Добавить линию тренда.
-
В окне Линия тренда выбираем тип линии тренда – Полиномиальная и устанавливаем степень – 2.
-
Во вкладке Параметры устанавливаем флажки в поля показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации.
-
График построен.
-
Нахождение min(max) функции, учитывая ограничения:
Для нахождения необходимо:
В ячейки А2, А3 и А4 занести константы неравенства числа 17, 34, 17, соответственно.
-
В ячейки С1 и D1 занесем начальные значения неизвестных х1, х2 (нули)- в дальнейшем эти значения будут подобраны автоматически.
-
В ячейках диапазона С2:D4 разместим таблицу значений при х1 и х2.
-
В ячейках В2:В4 укажем формулы для расчета. В ячейке В2 формула будет иметь вид = $C$1*C2+$D$1*D2, а остальные формулы получаем методом автозаполнения (копирования).
-
В ячейку F1 занесем формулу =4*х1+3*х2.
-
Команда Сервис – Поиск решения.
-
В поле Установить целевую ячейку, укажем значение F1.
-
В поле Изменяя ячейки зададим диапазон С1:D1.
-
Определяем набор ограничений, щелкнем на кнопку Добавить. В диалоговом окне Добавление ограничения в поле Ссылка на ячейку мышью укажем диапазон В2:В4. В качестве условия зададим <=. В поле ограничения зададим диапазон А2:А4. Нажимаем ОК.
-
Выбираем кнопку Выполнить. По завершении оптимизации откроется диалоговое окно Результаты поиска решения.
-
Сохраняем найденное решение.
Список литературы
-
Гельман В. Я. Решение математических задач средствами
Excel:СПб Питер,2003- 240 стр.
-
Excel: Сборник примеров и задач: Учеб. пособие для вузов.
ФиС,2008- 336 стр
