
математика даны вершины
.doc1. Элементы векторной алгебры и аналитической геометрии
1-10. Даны четыре вектора
![]() =(а1,а2,а3),
=(а1,а2,а3),
![]() =(b1,b2,b3),
=(b1,b2,b3),
![]() =(c1,c2,c3),
=(c1,c2,c3),
![]() =(d1,d2,d3)
в некотором базисе. Показать, что векторы
=(d1,d2,d3)
в некотором базисе. Показать, что векторы
![]() ,
,
![]() ,
,
![]() образуют
базис, и найти координаты вектора
образуют
базис, и найти координаты вектора
![]() в
этом базисе.
в
этом базисе.
1.
![]() =(1;1;0),
=(1;1;0),
![]() =(0;1;-2),
=(0;1;-2),
![]() =(1;0;3),
=(1;0;3),
![]() =(2;-1;11).
=(2;-1;11).
2.
![]() =(1;0;2),
=(1;0;2),
![]() =(-1;0;1),
=(-1;0;1),
![]() =(2;5;-3),
=(2;5;-3),
![]() =(11;5;-3).
=(11;5;-3).
3.
![]() =(2;0;1),
=(2;0;1),
![]() =(1;1;0),
=(1;1;0),
![]() =(4;1;2),
=(4;1;2),
![]() =(8;0;5).
=(8;0;5).
4.
![]() =(0;1;3),
=(0;1;3),
![]() =(1;2;-1),
=(1;2;-1),
![]() =(2;0;-1),
=(2;0;-1),
![]() =(3;1;8).
=(3;1;8).
5.
![]() =(1;2;-1),
=(1;2;-1),
![]() =(3;0;2),
=(3;0;2),
![]() c=(-1;1;1),
c=(-1;1;1),
![]() =(8;1;2).
=(8;1;2).
6.
![]() =(1;4;1),
=(1;4;1),
![]() =(-3;2;0),
=(-3;2;0),
![]() =(1;-1;2),
=(1;-1;2),
![]() =(-9;-8;3).
=(-9;-8;3).
7.
![]() =(0;1;-2),
=(0;1;-2),
![]() =(3;-1;1),
=(3;-1;1),
![]() =(4;1;0),
=(4;1;0),
![]() =(-5;9;-13).
=(-5;9;-13).
8.
![]() =(0;5;1),
=(0;5;1),
![]() =(3;2;-1),
=(3;2;-1),
![]() =(-1;1;0),
=(-1;1;0),
![]() =(-15;5;6).
=(-15;5;6).
9.
![]() =(1;0;1),
=(1;0;1),
![]() =(0;-2;1),
=(0;-2;1),
![]() =(1;3;0),
=(1;3;0),
![]() =(8;9;4).
=(8;9;4).
10.
![]() =(2;1;0),
=(2;1;0),
![]() =(1;0;1),
=(1;0;1),
![]() =(4;2;1),
=(4;2;1),
![]() =(3;1;3).
=(3;1;3).
11-20. Даны координаты вершин пирамиды А1, А2, А3, А4. Найти:1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1(1;3;0), А2(4;-1;2), А3(3;0;1), А4(-4;3;5).
12. А1(-2;-1;-1), А2(0;3;2), А3(3;1;-4), А4(-4;7;3).
13. А1(-3;-5;6), А2(2;1;-4), А3(0;-3;-1), А4(-5;2;-8).
14. А1(2;-4;-3), А2(5;-6;0), А3(-1;3;-3), А4(-10;-8;7).
15. А1(1;-1;2), А2(2;1;2), А3(1;1;4), А4(6;-3;8).
16. А1(9;5;5), А2(-3;7;1), А3(5;7;8), А4(6;9;2).
17. А1(0;7;1), А2(4;1;5), А3(4;6;3), А4(3;9;8).
18. А1(5;5;4), А2(3;8;4), А3(3;5;10), А4(5;8;2).
19. А1(6;1;1), А2(4;6;6), А3(4;2;0), А4(1;2;6).
20. А1(7;5;3), А2(9;4;4), А3(4;5;7), А4(7;9;6).
21. Даны две вершины треугольника А(2;2), В(3;0) и точка пересечения его медиан D(3;1). Найти координаты вершины С.
22. Дано уравнение одной из сторон квадрата x + 3y – 7 = 0 и точка пересечения его диагоналей Р(0;-1), найти уравнения трех остальных сторон квадрата.
23. Составить уравнения сторон треугольника АВС, если известны координаты его вершин А(-3;3), В(5;-1) и точка пересечения его высот М(4;3).
24. Найти координаты центра окружности, описанной около треугольника с вершинами А(0;5), В(1;-2), С(-6;5).
25. Даны уравнения двух сторон треугольника 4х – 5у + 9 = 0 и х + 4у – 3 = 0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке Р(3;1).
26. Составить уравнения сторон треугольника, если даны одна из его вершин В(-4;-5) и уравнения двух его высот 5х + 3у – 4 = 0 и 3х – 8у – 13 = 0.
27. Составить уравнения сторон треугольника, зная одну его вершину С(4;-1), а также уравнения высоты 2х – 3у + 12 = 0 и медианы 2х + 3у = 0.
28. Через точку М(4;3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Определить точки пересечения этой прямой с осями координат.
29. Даны две вершины треугольника А(-10;-13), В(-2;3) и С(2;1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
30. Даны уравнения двух сторон квадрата 4х – 3у + 3 = 0, 4х – 3у - 17 = 0 и одна из его вершин А(2;-3). Составить уравнения двух других сторон этого квадрата.
31. Составить уравнение линии, каждая точка которой равноудалена от точки А(4;4) и от оси абсцисс. Сделать чертеж.
32. Составить уравнение линии, каждая точка которой удалена от точки А(2;0) вдвое дальше, чем от оси ординат. Сделать чертеж.
33. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(-2;0), чем от точки В(1;0). Сделать чертеж.
34. Составить уравнение линии, расстояние каждой точки которой от начала координат и от прямой 3х + 16 = 0 относятся как 3 : 5. Сделать чертеж.
35. Составить уравнение линии, расстояния каждой точки которой от точек А(6;0) и В(2;0) относятся как 2 : 1. Сделать чертеж.
36. Составить уравнение линии, каждая точка которой отстоит от точки А(3;0) вдвое дальше, чем от прямой х = 1. Сделать чертеж.
37. Составить уравнение линии, расстояния каждой точки которой от точки А(-2;0) и от точки В(2;0) относятся как 3 : 4.Сделать чертеж.
38. Составить уравнение линии, каждая точка которой равноудалена от точки А(1;3) и от прямой у + 1 = 0. Сделать чертеж.
39. Составить уравнение линии, расстояние каждой точки которой от точки А(1;0) втрое больше расстояния от прямой у = -2. Сделать чертеж.
40. Составить уравнение линии, расстояние каждой точки которой от точки А(4;2) равно расстоянию от оси ординат. Сделать чертеж.
41-50. Линия задана уравнением
![]() в
полярной системе координат. Требуется:
в
полярной системе координат. Требуется:
1) построить линию по точкам, начиная от
![]() =
0 до
=
0 до
![]() и
придавая
и
придавая
![]() значения
через промежуток
значения
через промежуток
![]() ;
;
2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
41.
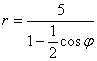 42.
42.
![]() 43.
43.
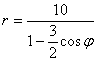 44.
44.
![]()
45.
![]() 46.
46.
![]() 47.
47.
![]() 48.
48.
![]()
49.
![]() 50.
50.
![]()
2. Элементы линейной алгебры
51-60. Дана система линейных уравнений
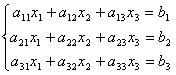
Доказать совместность системы и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51.
 52.
52.
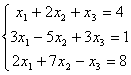 53.
53.
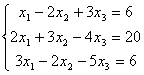
54.
 55.
55.
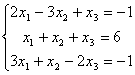 56.
56.
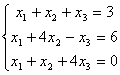
57.
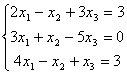 58.
58.
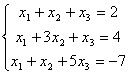 59.
59.
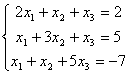
60.
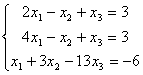
Средствами матричного исчисления найти
преобразование, выражающее
![]() ,
,
![]() ,
,
![]() через
через
![]() ,
,
![]() ,
,
![]() .
.
61.
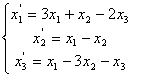
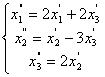 62.
62.
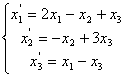

63.
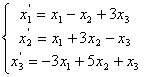
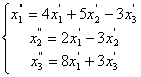
64.
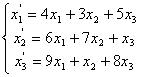
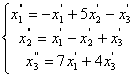
65.
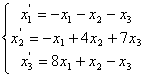
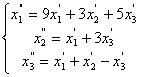
66.
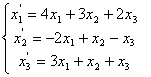
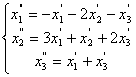
67.
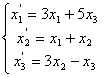
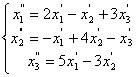
68.
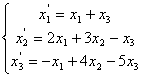
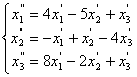
69.
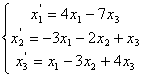
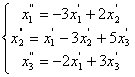
70.
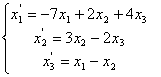
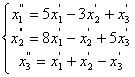
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
71.
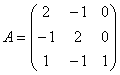 72.
72.
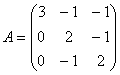 73.
73.
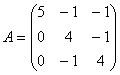 74.
74.
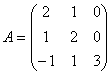
75.
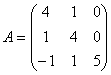 76.
76.
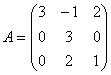 77.
77.
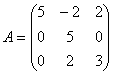 78.
78.
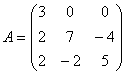
79.
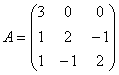 80.
80.
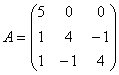
81-90. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка.
81.
![]() 82.
82.
![]() 83.
83.
![]()
84.
![]() 85.
85.
![]() 86.
86.
![]()
87.
![]() 88.
88.
![]() 89.
89.
![]()
90.
![]()
91-100. Дано комплексное число z. Требуется:
1) записать его в алгебраической и тригонометрической формах;
2) найти все корни уравнения
![]() .
.
91.
![]() 92.
92.
![]() 93.
93.
![]() 94.
94.
![]() 95.
95.
![]() 96.
96.
![]()
97.
![]() 98.
98.
![]() 99.
99.
![]() 100.
100.
![]()
3. Введение в математический анализ
101-110. а) найти область определения функции;
б,в) построить графики функций при помощи преобразований графиков
основных элементарных функций.
101. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
102. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
103. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
104. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
105. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
106. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
107. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
108. а)
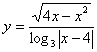 ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
109. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
110. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]()
111-120. Найти пределы функций, не пользуясь правилом Лопиталя.
111. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
112. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
113. а)
![]() ;
б)
;
б)
![]() ;
;
в)
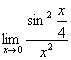 ;
г)
;
г)
![]() .
.
114. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
115. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
116. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
117. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
118. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
119. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
120. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
121-130. Заданы функция
![]() и
два значения аргумента х1
и х2. Требуется: 1) установить,
является ли данная функция непрерывной
или разрывной для каждого из данных
значений аргумента; 2) в случае разрыва
функции найти ее пределы слева и справа;
3) сделать схематический чертеж.
и
два значения аргумента х1
и х2. Требуется: 1) установить,
является ли данная функция непрерывной
или разрывной для каждого из данных
значений аргумента; 2) в случае разрыва
функции найти ее пределы слева и справа;
3) сделать схематический чертеж.
121.
![]() 122.
122.
![]() .
.
123.
![]() .
124.
.
124.
![]() .
.
125.
![]() .
126.
.
126.
![]() .
.
127.
![]() .
128.
.
128.
![]() .
.
129.
![]() .
130.
.
130.
![]()
131-140. Задана функция
![]() .
Найти точки разрыва, если они существуют.
Сделать схематический чертеж.
.
Найти точки разрыва, если они существуют.
Сделать схематический чертеж.
131.
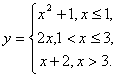 132.
132.
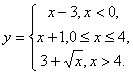 133.
133.
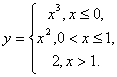
134.
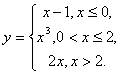 135.
135.
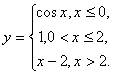 136.
136.

137.
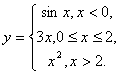 138.
138.
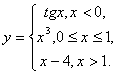 139.
139.

140.
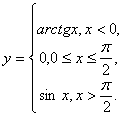
4. Производная и ее приложения
141-150. Найти производные
![]() данных
функций.
данных
функций.
141. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
142. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
143. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
144. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
145. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
146. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
147. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
