
Дифференциальное исчисление функций
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ В ТОЧКЕ
Пусть
функция
 определена в точке
определена в точке и некоторой ее окрестности. Придадим
аргументу
и некоторой ее окрестности. Придадим
аргументу приращение
приращение такое, что точка
такое, что точка попадает в область определения функции.
Функция при этом получит приращение
попадает в область определения функции.
Функция при этом получит приращение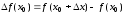 .
.
ОПРЕДЕЛЕНИЕ.
Производной
функции
 в точке
в точке называется предел отношения приращения
функции в этой точке к приращению
аргумента
называется предел отношения приращения
функции в этой точке к приращению
аргумента
 ,
при
,
при (если этот предел существует и конечен),
т.е.
(если этот предел существует и конечен),
т.е.
 .
.
Обозначают:
 ,
, ,
, ,
, .
.
Производной
функции
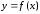 в точке
в точке справа (слева)
называется
справа (слева)
называется


(если этот предел существует и конечен).
Обозначают:
 ,
, – производная
– производная в точке
в точке справа,
справа,
 ,
, – производная
– производная в точке
в точке слева.
слева.
Очевидно, что справедлива следующая теорема.
ТЕОРЕМА.
Функция
 имеет производную в точке
имеет производную в точке тогда и только тогда, когда в этой точке
существуют и равны между собой производные
функции справа и слева. Причем
тогда и только тогда, когда в этой точке
существуют и равны между собой производные
функции справа и слева. Причем
 .
.
Следующая
теорема устанавливает связь между
существованием производной функции в
точке
 и непрерывностью функции в этой точке.
и непрерывностью функции в этой точке.
ТЕОРЕМА
(необходимое условие существования
производной функции в точке). Если
функция
 имеет производную в точке
имеет производную в точке ,
то функция
,
то функция в этой точке непрерывна.
в этой точке непрерывна.
ДОКАЗАТЕЛЬСТВО
Пусть
существует

 .
Тогда
.
Тогда
 ,
,
где
 – бесконечно малая при
– бесконечно малая при .
.
⇒
 ;
;
⇒

 .
.
Но
это означает, что
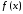 непрерывна в точке
непрерывна в точке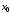 (см. геометрическое определение
непрерывности). ∎
(см. геометрическое определение
непрерывности). ∎
Замечание.
Непрерывность функции в точке
 не является достаточным условием
существования производной этой функции
в точке
не является достаточным условием
существования производной этой функции
в точке .
Например, функция
.
Например, функция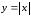 непрерывна, но не имеет производной в
точке
непрерывна, но не имеет производной в
точке .
Действительно,
.
Действительно,

 ,
,

 ,
,
и,
следовательно,
 не существует.
не существует.
Очевидно,
что соответствие
 является функцией, определенной на
некотором множестве
является функцией, определенной на
некотором множестве .
Ее называютпроизводной
функции
.
Ее называютпроизводной
функции
 и обозначают
и обозначают
 ,
,
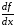 ,
, ,
, .
.
Операцию
нахождения для функции
 ее производной функции называютдифференцированием
функции
ее производной функции называютдифференцированием
функции
 .
.
ГЕОМЕТРИЧЕЧКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ
1)
Физический
смысл производной.
Если функция
 и ее аргумент
и ее аргумент являются физическими величинами, то
производная
являются физическими величинами, то
производная – скорость изменения переменной
– скорость изменения переменной относительно переменной
относительно переменной в точке
в точке .
Например, если
.
Например, если – расстояние, проходимое точкой за
время
– расстояние, проходимое точкой за
время ,
то ее производная
,
то ее производная – скорость в момент времени
– скорость в момент времени .
Если
.
Если – количество электричества, протекающее
через поперечное сечение проводника в
момент времени
– количество электричества, протекающее
через поперечное сечение проводника в
момент времени ,
то
,
то – скорость изменения количества
электричества в момент времени
– скорость изменения количества
электричества в момент времени ,
т.е. сила тока в момент времени
,
т.е. сила тока в момент времени .
.
2) Геометрический смысл производной.
Пусть
 – некоторая кривая,
– некоторая кривая, – точка на кривой
– точка на кривой .
.
Любая
прямая, пересекающая
 не менее чем в двух точках называетсясекущей.
не менее чем в двух точках называетсясекущей.
Касательной
к кривой
 в точке
в точке называется предельное положение секущей
называется предельное положение секущей
 ,
если точка
,
если точка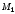 стремится к
стремится к ,
двигаясь по кривой.
,
двигаясь по кривой.
Из
определения очевидно, что если касательная
к кривой в точке
 существует, то она единственная
существует, то она единственная
Рассмотрим
кривую
 (т.е. график функции
(т.е. график функции ).
Пусть в точке
).
Пусть в точке он имеет невертикальную касательную
он имеет невертикальную касательную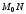 .
Ее уравнение:
.
Ее уравнение: (уравнение прямой, проходящей через
точку
(уравнение прямой, проходящей через
точку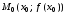 и имеющую угловой коэффициент
и имеющую угловой коэффициент ).
).
По определению углового коэффициента
 ,
,
где
 – угол наклона прямой
– угол наклона прямой к оси
к оси .
.
Пусть
 – угол наклона секущей
– угол наклона секущей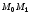 к оси
к оси ,
где
,
где .
Так как
.
Так как – касательная, то при
– касательная, то при

 ,
,
⇒
 ,
,
⇒
 .
.
Следовательно,
 .
.
Таким
образом, получили, что
 – угловой коэффициент касательной к
графику функции
– угловой коэффициент касательной к
графику функции
 в точке
в точке (геометрический смысл производной
функции в точке). Поэтому уравнение
касательной к кривой
(геометрический смысл производной
функции в точке). Поэтому уравнение
касательной к кривой
 в точке
в точке можно записать в виде
можно записать в виде

Замечание.
Прямая, проходящая через точку
 перпендикулярно касательной, проведенной
к кривой в точке
перпендикулярно касательной, проведенной
к кривой в точке ,
называетсянормалью
к кривой в точке
,
называетсянормалью
к кривой в точке
 .
Так как угловые коэффициенты
перпендикулярных прямых связаны
соотношением
.
Так как угловые коэффициенты
перпендикулярных прямых связаны
соотношением
 ,
то уравнение нормали к кривой
,
то уравнение нормали к кривой в точке
в точке будет иметь вид
будет иметь вид
 ,
если
,
если
 .
.
Если
же
 ,
то касательная к кривой
,
то касательная к кривой в точке
в точке будет иметь вид
будет иметь вид
 ,
,
а
нормаль  .
.
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ
Уравнение касательной
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:
y/(x)=limΔx→0ΔyΔx
Δy=f(x+Δx)−f(x).
Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.

Уравнение нормали
Нормаль - это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
ТЕОРЕМА (необходимое условие существования производной функции в точке). Если функция
 имеет производную в точке
имеет производную в точке ,
то функция
,
то функция в этой точке непрерывна.
в этой точке непрерывна.
ДОКАЗАТЕЛЬСТВО
Пусть
существует

 .
Тогда
.
Тогда
 ,
,
где
 – бесконечно малая при
– бесконечно малая при .
.
⇒
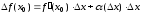 ;
;
⇒

 .
.
Но
это означает, что
 непрерывна в точке
непрерывна в точке (см. геометрическое определение
непрерывности). ∎
(см. геометрическое определение
непрерывности). ∎
Замечание.
Непрерывность функции в точке
 не является достаточным условием
существования производной этой функции
в точке
не является достаточным условием
существования производной этой функции
в точке .
Например, функция
.
Например, функция непрерывна, но не имеет производной в
точке
непрерывна, но не имеет производной в
точке .
Действительно,
.
Действительно,

 ,
,

 ,
,
и,
следовательно,
 не существует.
не существует.
Очевидно,
что соответствие
 является функцией, определенной на
некотором множестве
является функцией, определенной на
некотором множестве .
Ее называютпроизводной
функции
.
Ее называютпроизводной
функции
 и обозначают
и обозначают
 ,
,
 ,
,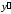 ,
, .
.
Операцию
нахождения для функции
 ее производной функции называютдифференцированием
функции
ее производной функции называютдифференцированием
функции
 .
.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
