Прямой, обратный и дополнительный двоичные коды
В компьютерной арифметике, которая базируется на двоичной системе счисления, операция «вычитания» заменяется операцией «сложения».
Рассмотрим, как это происходит.
Для хранения целых чисел в памяти ЭВМ выделяется фиксированное число двоичных разрядов – бит. Рассмотрим 8–и битовое представление числа. Каждый бит нумеруется «слева – направо» от 0 до 7.
вес разряда
нумерация бит в
байте
|
|
26 |
25 |
24 |
23 |
22 |
21 |
20 |
7 6 5 4 3 2 1 0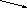
Старший бит – седьмой – используется для знака числа: 0 – это положительное число, 1 – отрицательное.
Если в разрядах байта с 0 по 6 поместить абсолютное значение числа, а в 7-ом бите установить его знак (0 или 1), то полученное представление числа называется прямым двоичным кодом.
Если в прямом коде число представлено как отрицательное (7-ой бит равен 1), то в числе инвертируются 2все разряды, кроме знакового. Такое представление числа называетсяобратный двоичный код.
После прибавления к обратному коду 1 получается дополнительный двоичный код.
Использование дополнительного двоичного кода позволяет создавать схемы, выполняющие вычитание, умножение и деление посредством операции сложения.
Рассмотрим на примерах операцию вычитания для 8-и битовых чисел.
ПРИМЕР 1:Вычесть число 3 из 5 (1012 – 0112).
Запишем абсолютное значение числа -3 в байте
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
В знаковый – седьмой – бит запишем признак отрицательности числа 1 и получим прямой двоичный код числа -3.
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Инвертируем все разряды в числе, кроме знакового
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Получим обратный двоичный код числа -3.
Прибавим к обратному коду единицу
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Получим дополнительный двоичный код числа -3.
Сложим число 5 и дополнительный двоичный код числа -3
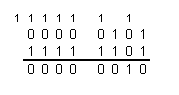
Получили число 0102 = 210.
Ответ:1012 – 0112 = 0102
Проверка:Сделаем проверку, преобразуя двоичные числа к десятичному виду:
510 – 310 = 210
ПРИМЕР 2:Вычесть число 49 из 63
Прямой двоичный код числа -49
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Инверсный код числа -49 (обратный двоичный код)
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Дополнительный код числа -49
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Сложим число 63 и дополнительный код числа -49
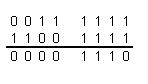
Получили число 11102 = 1410
Ответ: 11 11112 – 11 00012 = 11102
Проверка: 6310 – 4910 = 1410
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.Используя схемы примера 1 или 2, сделайте вычитание целых чисел, используя дополнительный двоичный код.
|
Номер варианта |
Числа |
Номер варианта |
Числа |
|
1 |
81 и 17 |
9 |
64 и 32 |
|
2 |
42 и 18 |
10 |
51 и 28 |
|
3 |
42 и 36 |
11 |
92 и 48 |
|
4 |
61 и 28 |
12 |
67 и 29 |
|
5 |
74 и 28 |
13 |
82 и 29 |
|
6 |
62 и 39 |
14 |
53 и 29 |
|
7 |
43 и 28 |
15 |
83 и 38 |
|
8 |
78 и 49 |
16 |
68 и 29 |