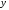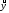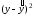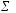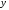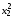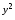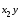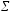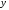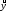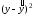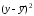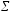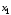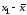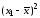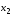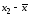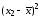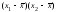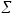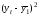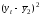8. Проанализируем статистическую значимость коэффициентов множественного уравнения с надежностью 0,95. Расчетное значение t-критерия вычислим по формуле:

,

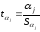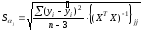
где 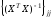- диагональный элемент матрицы .

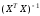166	165,982	0,000
158	157,568	0,187
155	156,307	1,708
177	174,998	4,008
130	131,121	1,258
155	154,734	0,071
172	171,762	0,057
143	142,370	0,397
122	121,793	0,043
149	148,323	0,459
180	180,120	0,014
178	179,205	1,452
150	150,125	0,016
158	158,656	0,430
154	155,281	1,640
126	125,743	0,066
123	123,255	0,065
155	154,276	0,524
128	127,489	0,261
130	129,894	0,011
166	165,982	0,000
158	157,568	0,187
		12,666

,

,

, , ,

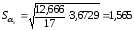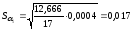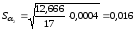
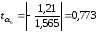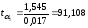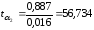Найдем табличное значение критерия:

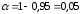
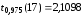
Так как расчетные значения t-критерия параметров 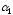и 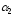больше табличного значения, то эти параметры уравнения множественной регрессии являются статистически значимыми. Расчетное значение t-критерия параметра 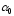меньше табличного значения, значит, этот параметр уравнения множественной регрессии не является статистически значимым.

9. Найдем коэффициенты парной корреляции. Коэффициент корреляции между валовым доходом и стоимостью основных фондов найден в п. 2:

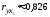
Значение коэффициента корреляции говорит о наличии между валовым доходом и стоимостью основных фондов тесной прямой линейной связи.

Аналогично найдем коэффициент парной корреляции между валовым доходом и стоимостью оборотных средств:

№	x2
1	70	166	4900	27556	11620
2	64	158	4096	24964	10112
3	80	155	6400	24025	12400
4	61	177	3721	31329	10797
5	76	130	5776	16900	9880
6	73	155	5329	24025	11315
7	80	172	6400	29584	13760
8	73	143	5329	20449	10439
9	62	122	3844	14884	7564
10	71	149	5041	22201	10579
11	72	180	5184	32400	12960
12	64	178	4096	31684	11392
13	80	150	6400	22500	12000
14	60	158	3600	24964	9480
15	44	154	1936	23716	6776
16	56	126	3136	15876	7056
17	41	123	1681	15129	5043
18	69	155	4761	24025	10695
19	51	128	2601	16384	6528
20	45	130	2025	16900	5850
	1292	3009	86256	459495	196246

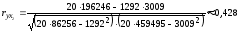
Значение коэффициента корреляции говорит о наличии между валовым доходом и стоимостью оборотных средств заметной прямой линейной связи.

Найдем общий коэффициент детерминации:

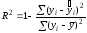
Рассчитаем фактическое значение при :

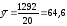166	165,982	0,000		241,803
158	157,568	0,187		57,003
155	156,307	1,708		20,703
177	174,998	4,008		704,903
130	131,121	1,258		418,203
155	154,734	0,071		20,703
172	171,762	0,057		464,403
143	142,370	0,397		55,502
122	121,793	0,043		809,402
149	148,323	0,459		2,102
180	180,120	0,014		873,203
178	179,205	1,452		759,003
150	150,125	0,016		0,202
158	158,656	0,430		57,003
154	155,281	1,640		12,603
126	125,743	0,066		597,802
123	123,255	0,065		753,502
155	154,276	0,524		20,703
128	127,489	0,261		504,002
130	129,894	0,011		418,203
166	165,982	0,000		241,803
158	157,568	0,187		57,003
			12,666	6790,95

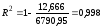
Найдем частные коэффициенты корреляции:

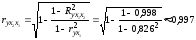
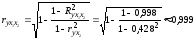
Таким образом, более тесная связь наблюдается между валовым доходом среднегодовой стоимостью оборотных средств.

10. Общий коэффициент детерминации был найден в предыдущем пункте:

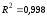
Найдем скорректированный коэффициент детерминации:

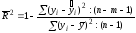
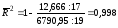
Значение скорректированного коэффициента детерминации совпадает со значением общего.

11. Оценим адекватность уравнения регрессии с помощью F-теста. Проверим гипотезу Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Так как регрессия множественная (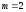), то фактическое значение F-статистики Фишера вычислим по формуле:

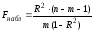
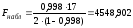
Найдем табличное значение критерия:

,

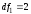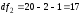
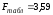
Так как табличное значение критерия меньше расчетного 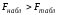, то гипотезу Н₀ отклоняем, то есть данное уравнение регрессии является статистически значимым.

12. Дадим точечный и интервальный прогноз с надежностью 0,95 величины валового дохода для предприятия, на котором стоимость основных фондов составляет 50 млн. руб., а стоимость оборотных средств - 75 млн. руб.:

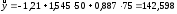млн. руб.

Сделаем интервальный прогноз с надежностью 0,95:

,

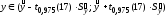
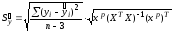где 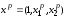- вектор независимых переменных, для которого определяется интервал; .

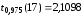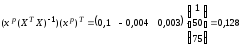
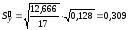
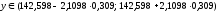
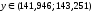
13. Проверим построенное уравнение на наличие мультиколлинеарности по критерию Стьюдента. Для определения мультиколлинеарности найдем коэффициент корреляции :

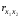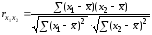
68	6,950	48,303	70	5,40	29,160	37,5300
66	4,950	24,503	64	-0,60	0,360	-2,9700
56	-5,050	25,503	80	15,40	237,160	-77,7700
79	17,950	322,203	61	-3,60	12,960	-64,6200
42	-19,050	362,903	76	11,40	129,960	-217,1700
59	-2,050	4,202	73	8,40	70,560	-17,2200
66	4,950	24,503	80	15,40	237,160	76,2300
51	-10,050	101,003	73	8,40	70,560	-84,4200
44	-17,050	290,703	62	-2,60	6,760	44,3300
56	-5,050	25,503	71	6,40	40,960	-32,3200
76	14,950	223,503	72	7,40	54,760	110,6300
80	18,950	359,103	64	-0,60	0,360	-11,3700
52	-9,050	81,902	80	15,40	237,160	-139,3700
69	7,950	63,203	60	-4,60	21,160	-36,5700
76	14,950	223,503	44	-20,60	424,360	-307,9700
50	-11,050	122,103	56	-8,60	73,960	95,0300
57	-4,050	16,403	41	-23,60	556,960	95,5800
61	-0,050	0,002	69	4,40	19,360	-0,2200
54	-7,050	49,703	51	-13,60	184,960	95,8800
59	-2,050	4,202	45	-19,60	384,160	40,1800
68	6,950	48,303	70	5,40	29,160	37,5300
66	4,950	24,503	64	-0,60	0,360	-2,9700
		2372,95			2792,8	-396,6

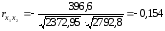
Проверим, что этот коэффициент незначимо отличается от нуля:

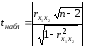
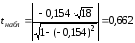
Расчетное значение критерия по модулю меньше табличного, поэтому можно считать, что переменные 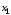и 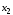не коррелирует между собой и, следовательно, мультиколлинеарность остутствует.

Для проверки по критерию «хи-квадрат» χ² на уровне значимости 0,1 найдем определитель матрицы коэффициентов парной корреляции:

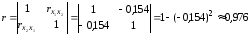
Вычислим χ²-критерий:

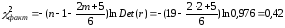
Найдем табличное значение χ² пр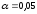и и 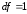: 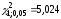. Так как 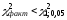, то в соответствии с критерием Пирсона мультиколлинеарность отсутствует.

Таким образом, и тот и другой критерий показали отсутствие мультиколлинеарности.

Ситуационная (практическая) задача № 2

Динамика выпуска продукции за 1994-2011 гг. представлена в таблице.

Год	Выпуск , ед	Год	Выпуск, ед	Год	Выпуск, ед
1994	35	2000	52	2006	57
1995	40	2001	45	2007	55
1996	37	2002	48	2008	52
1997	39	2003	50	2009	51
1998	40	2004	55	2010	54
1999	47	2005	50	2011	58

Требуется:

1. 1. Проверить гипотезу о наличии тренда во временном ряде.

2. 2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3. 3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99.

4. 4. Дать точечный и интервальный прогноз выпуска продукции на 2012 г. с надежностью 0,99.

Решение:

1. Проверим гипотезу о наличии тренда во временном ряде.

,

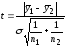где

,

,

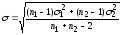
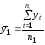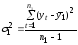
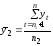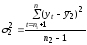
1	35	57,086	10	50	12,642
2	40	6,531	11	55	2,086
3	37	30,864	12	50	12,642
4	39	12,642	13	57	11,864
5	40	6,531	14	55	2,086
6	47	19,753	15	52	2,420
7	52	89,198	16	51	6,531
8	45	5,975	17	54	0,198
9	48	29,642	18	58	19,753
	383	258		482	70,222

,

,

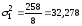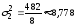
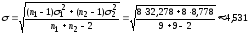
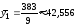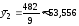
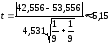
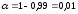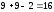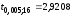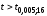Критическим значением критерия Стьюдента при уровне значимости и числе степеней свободы является . Так как , то гипотезу об отсутствии тренда отклоняем, то есть тренд есть.