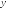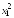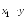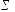1.Практическая часть.

Задача № 1

Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 20 торговым предприятиям были получены данные, приведенные в таблице:

№ пред-приятия	Валовой доход за год, y, млн.руб.	Среднегодовая стоимость, млн. руб.		№ пред-приятия	Валовой доход за год, y, млн.руб. основных фондов	Среднегодовая стоимость, млн. руб.
		основных фондов	оборотных средств			основных фондов	оборотных средств
1	166	68	70	11	180	76	72
2	158	66	64	12	178	80	64
3	155	56	80	13	150	52	80
4	177	79	61	14	158	69	60
5	130	42	76	15	154	76	44
6	155	59	73	16	126	50	56
7	172	66	80	17	123	57	41
8	143	51	73	18	155	61	69
9	122	44	62	19	128	54	51
10	149	56	71	20	130	59	45

Требуется:

1. Построить корреляционное поле между валовым доходом и стоимостью основных фондов. Выдвинуть гипотезу о тесноте и виде зависимости между этими показателями.

2. Оценить тесноту линейной связи между валовым доходом и стоимостью основных фондов с надежностью 0,95.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости валового дохода от стоимости основных фондов.

4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,95 и построить для них доверительные интервалы.

5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,95.

6. Дать точечный и интервальный прогноз с надежностью 0,95 величины валового дохода для предприятия с основными фондами 50 млн. руб.

7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.

8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,95 и построить для них доверительные интервалы.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,95.

12. Дать точечный и интервальный прогноз с надежностью 0,95 величины валового дохода для предприятия, на котором стоимость основных фондов составляет 50 млн. руб., а стоимость оборотных средств - 75 млн. руб.

13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Решение:

1. Построим корреляционное поле между валовым доходом и стоимостью основных фондов:

Видим, что с увеличением стоимости основных фондов валовые доходы растут, поэтому можно предположить, что между среднегодовой стоимостью основных фондов X₁ и валовыми доходами Y существует тесная линейная зависимость 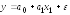, направление связи прямое.

2. Оценим тесноту линейной связи между валовым доходом и стоимостью основных фондов с помощью коэффициента линейной корреляции:

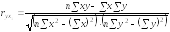
Заполним расчетную таблицу:

№	x1
1	68	166	4624	27556	11288
2	66	158	4356	24964	10428
3	56	155	3136	24025	8680
4	79	177	6241	31329	13983
5	42	130	1764	16900	5460
6	59	155	3481	24025	9145
7	66	172	4356	29584	11352
8	51	143	2601	20449	7293
9	44	122	1936	14884	5368
10	56	149	3136	22201	8344
11	76	180	5776	32400	13680
12	80	178	6400	31684	14240
13	52	150	2704	22500	7800
14	69	158	4761	24964	10902
15	76	154	5776	23716	11704
16	50	126	2500	15876	6300
17	57	123	3249	15129	7011
18	61	155	3721	24025	9455
19	54	128	2916	16384	6912
20	59	130	3481	16900	7670
	1221	3009	76915	459495	187015

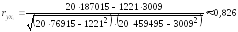
Значение коэффициента корреляции говорит о наличии между валовым доходом и стоимостью основных фондов тесной прямой линейной связи.

Сделаем проверку значимости найденного коэффициента корреляции с помощью t-критерия Стьюдента:

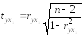
Найдем табличное значение t-критерия:

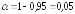
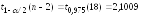
Так как 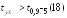, то с надежностью 0,95 можно утверждать, что коэффициент корреляции 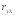является статистически значимым.

3. Рассчитаем коэффициенты линейного уравнения регрессии для зависимости валового дохода от стоимости основных фондов. В соответствии с методом наименьших квадратов расчет произведем по формулам:

,

,

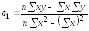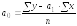
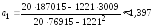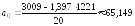
Получили линейное уравнение регрессии для зависимости Y(Х₁):

4. Проверим статистическую значимость параметров полученного уравнения регрессии с надежностью 0,95. Выдвинем гипотезу Н₀: 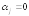о незначимом отклонении от нуля каждого отдельного параметра модели. Эта гипотеза отклоняется при .

,

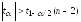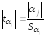
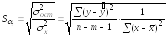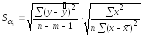
Рассчитаем значение критерия при

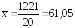
	x
1	68	48,30	166	160,161	34,097
2	66	24,50	158	157,366	0,402
3	56	25,50	155	143,394	134,699
4	79	322,20	177	175,530	2,160
5	42	362,90	130	123,833	38,034
6	59	4,20	155	147,586	54,972
7	66	24,50	172	157,366	214,146
8	51	101,00	143	136,408	43,456
9	44	290,70	122	126,627	21,412
10	56	25,50	149	143,394	31,427
11	76	223,50	180	171,339	75,021
12	80	359,10	178	176,927	1,150
13	52	81,90	150	137,805	148,716
14	69	63,20	158	161,558	12,659
15	76	223,50	154	171,339	300,625
16	50	122,10	126	135,011	81,192
17	57	16,40	123	144,791	474,858
18	61	0,00	155	150,380	21,343
19	54	49,70	128	140,600	158,749
20	59	4,20	130	147,586	309,256
		2372,95			2158,374

,

,

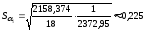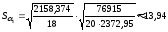
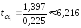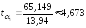
Так как оба расчетных значения t-критерия больше табличного значения 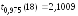, то параметры уравнения регрессии являются статистически значимыми.

Построим доверительный интервал для коэффициента :

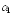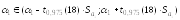
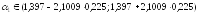
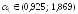
Построим доверительный интервал для коэффициента :

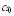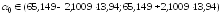
5. Рассчитаем коэффициент детерминации. Так как регрессия парная, то

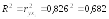
Оценим качество уравнения регрессии с помощью F-критерия Фишера. Проверим гипотезу Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Рассчитаем фактическое значение F-статистики Фишера. Так как регрессия парная, то фактическое значение найдем по формуле:

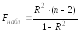
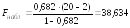
Определим табличное значение критерия:

,

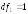Так как табличное значение меньше фактического 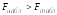, то гипотезу Н₀ отклоняем, то есть данное уравнение регрессии является статистически значимым.

6. Дадим точечный прогноз валового дохода, если среднегодовая стоимость основных фондов составит 50 млн. руб.:

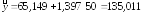млн. руб.

Составим интервальный прогноз с надежностью 0,95:

,

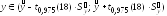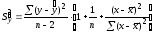
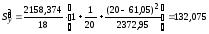
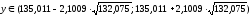
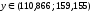
7. Рассчитаем коэффициенты линейного уравнения множественной регрессии. В соответствии с методом наименьших квадратов оценки параметров множественной линейной регрессионной модели вычислим по формуле:

,

где Х – матрица размером 20х3, первый столбец которой является единичным, а два других представляют собой значения 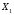и :

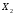Y – столбец значений 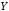. Тогда:

, ,

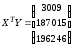
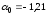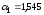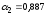
Получили уравнение множественной регрессии:

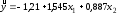
Поясним экономический смысл его параметров. Свободный коэффициент уравнения множественной регрессии, равный -1,21, показывает значение валового дохода при нулевой среднегодовой стоимости основных фондов и нулевой среднегодовой стоимости оборотных средств (в данном случае интерпретация свободного коэффициента не имеет экономического смысла). Коэффициент уравнения 1,545 показывает, что при неизменной среднегодовой стоимости оборотных средств увеличение (уменьшение) среднегодовой стоимости основных фондов на 1 млн. руб. может увеличить (уменьшить) валовой доход на 1,545 млн. руб., а коэффициент уравнения 0,887 показывает, что при неизменной среднегодовой стоимости основных фондов увеличение (уменьшение) среднегодовой стоимости оборотных средств на 1 млн. руб. может увеличить (уменьшить) валовой доход на 0,887 млн. руб.