Вариант № 4
Ситуационная (практическая) задача № 1
Исследовать и
построить график функции
Ситуационная (практическая) задача № 2
Исследовать на экстремум функцию двух переменных
z = x - xy + y - 2x + 4y + 1
Тестовые задания
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. Найти
производную функции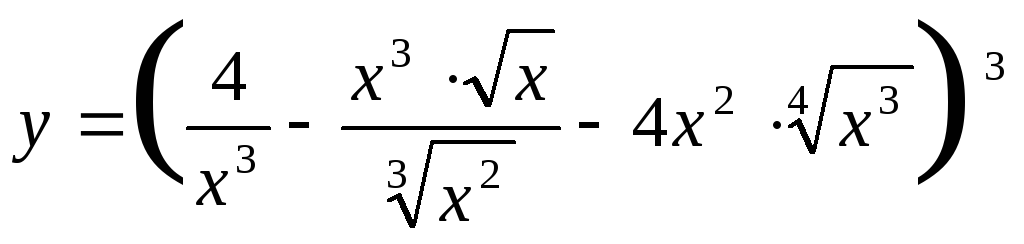 
А.
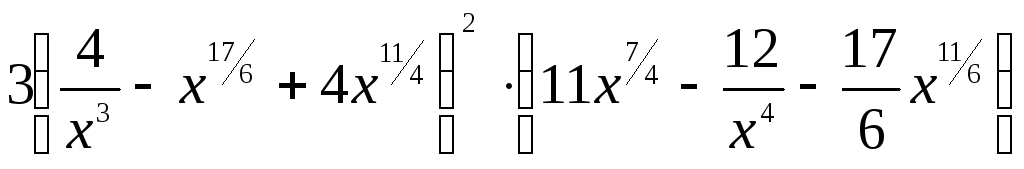
Б.
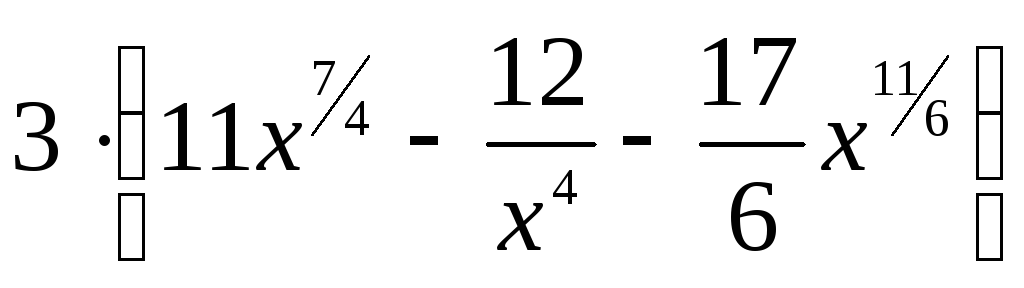
В.
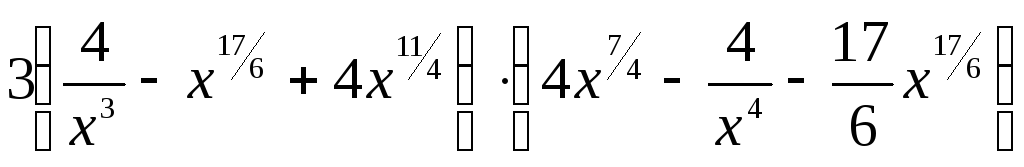
Г.
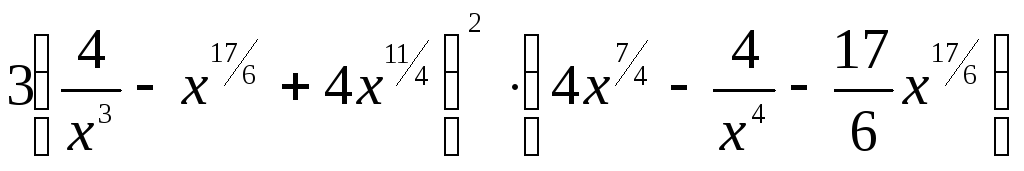
2. Найти
производную функции 
А.
Б.
В.
Г.
3. Найти
производную функции 
А.
Б.
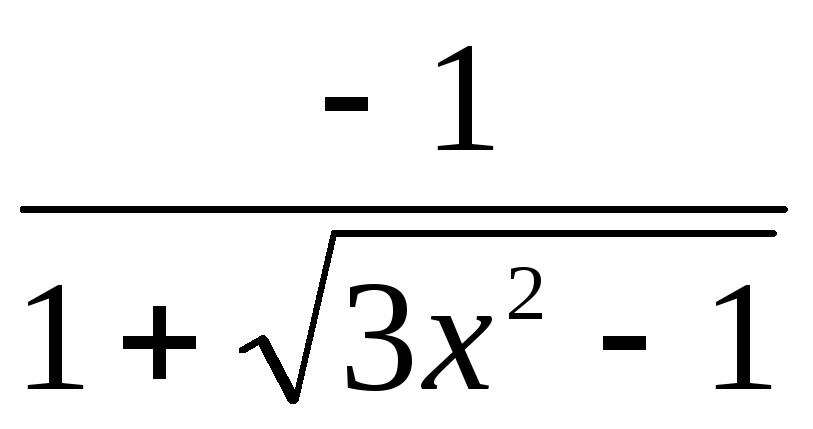
В.
Г.
4. Найти
производную функции 
А.
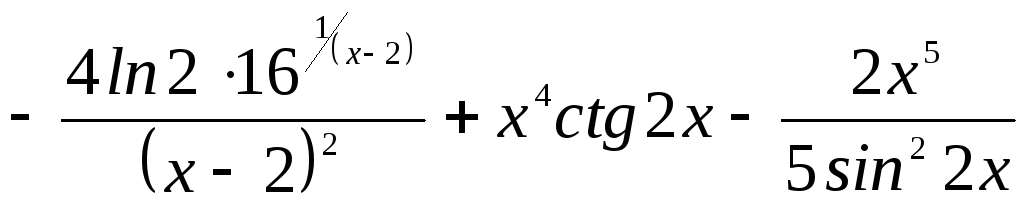
Б.
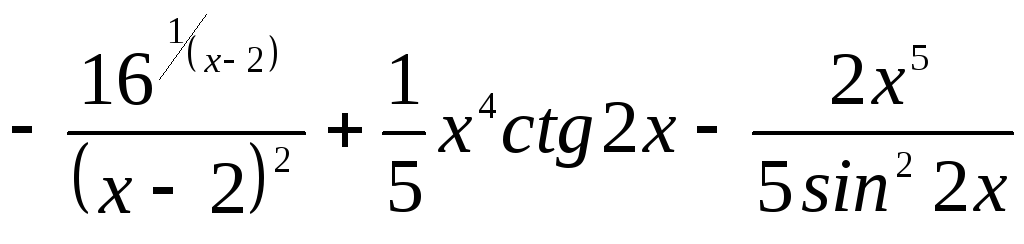
В.
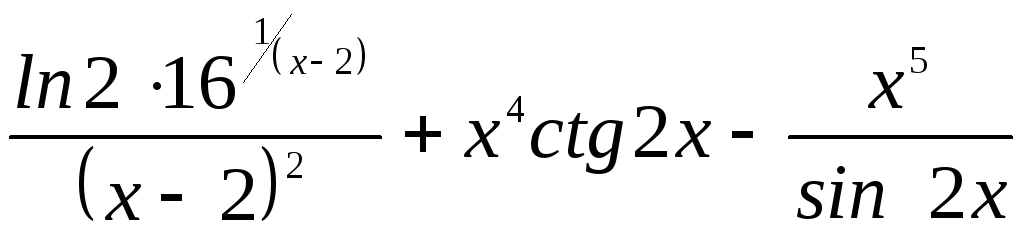
Г.
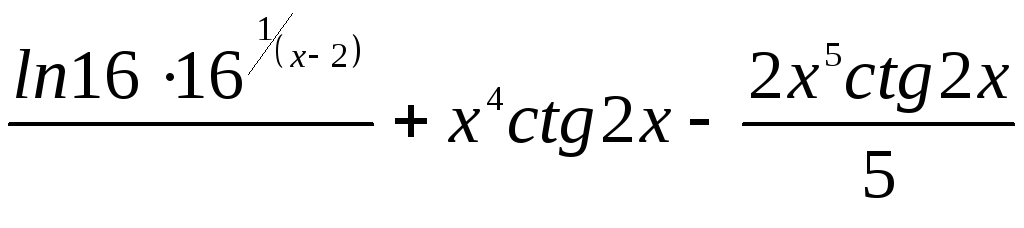
5. Функция
имеет минимум в точке с координатами
А. (1; 4)
Б. (-1; 1)
В. (0; 2)
Г. (-1; 0)
6.
Наклонная асимптота для графика функции
имеет вид
А. у = 1
Б. у = –1
В. у = 2
Г. у = –3
7. Выражение
вида
для функцииz
= 6x
- 12xy
+ 4y
+ 12 x
- 6y
+ 4 является
А.
Б.
В.
Г.
8. Для
функции
найти значение частной производной пох
в точке
:
А. 3
Б. -4
В. 4
Г. 2
9.
Найти
для
функции
А.
Б.
В.
Г.
10.
Для функции
найти значение
смешанной производной в точке А (–2,
2).
А. 2
Б. –4
В. –18
Г. 3
Вариант № 5
Ситуационная (практическая) задача № 1
Исследовать и
построить график функции
Ситуационная (практическая) задача № 2
Исследовать на экстремум функцию двух переменных
z = -3x + 2xy - 4y + 2x - 8y + 1.
Тестовые задания
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. Найти
производную функции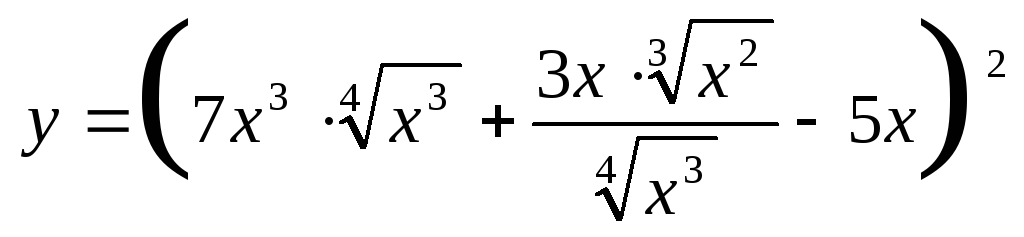 
А.
Б.
В.
Г.
2. Найти
производную функции 
А.
Б.
В.
Г.
3. Найти
производную функции 
А.
Б.
В.
Г.
4. Найти
производную функции 
А.
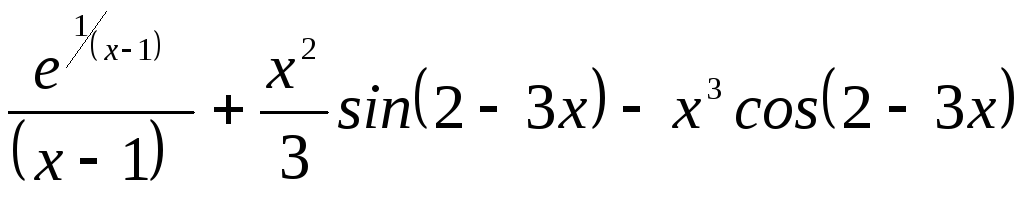
Б.
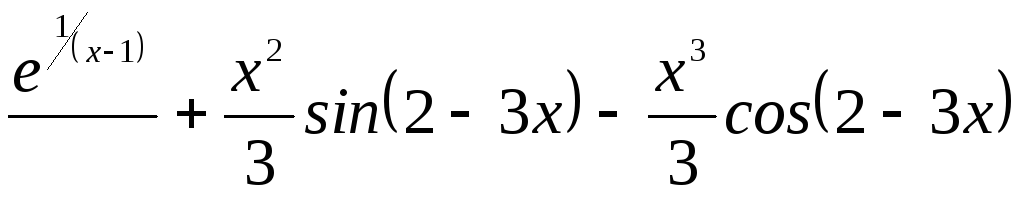
В.
Г.
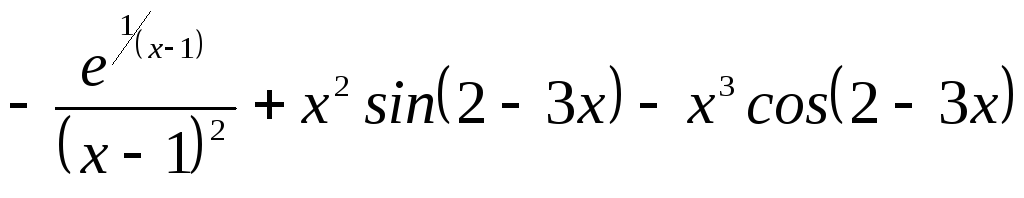
5.
Функция
имеет максимум в точке с координатами
А. (0; 5)
Б. (1; 6)
В. (-1; 10)
Г. (-2; 33)
6.
Наклонная асимптота для графика функции
имеет вид
А. у = 1
Б. у = –1
В. у = 4
Г. у = –3
7. Выражение
вида
для функцииz
= -2x
- 4xy
- 4y
- 4x
- 4y
+ 2 является
А.
Б.
В.
Г.
8. Для
функции
найти значение частной производной пох
в точке
А. 10
Б. 20
В. 30
Г. 40
9.
Найти
для
функции
А.
Б.
В.
Г.
10.
Для функции
найти значение
смешанной производной в точке А (–1,
2).
А. 4
Б. –20
В. –3
Г. 3
Вариант № 6
Ситуационная (практическая) задача № 1
Исследовать и
построить график функции
Ситуационная (практическая) задача № 2
Исследовать на экстремум функцию двух переменных
z
= -3x
- 3xy
- 4y
+ 3x
- 8y
– 3
Тестовые задания
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. Найти
производную функции 
А.
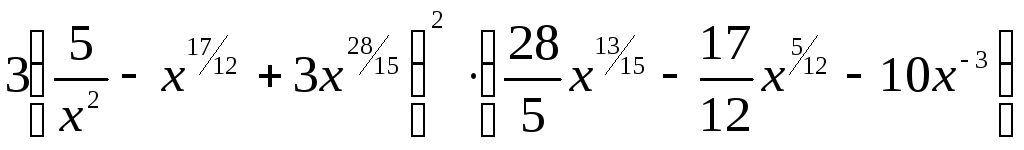
Б.
В.
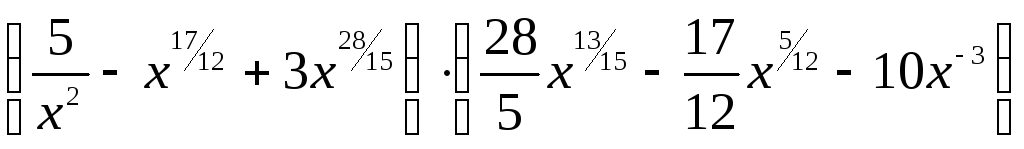
Г.
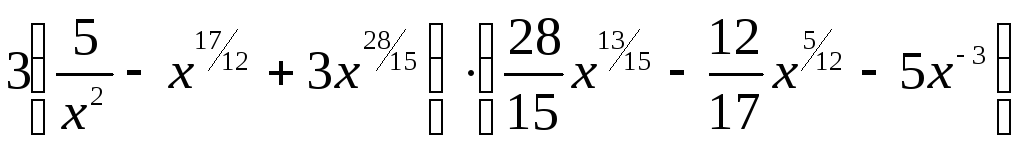
2. Найти
производную функции 
А.
Б.
В.
Г.
3.
Найти
производную функции 
А.
Б.
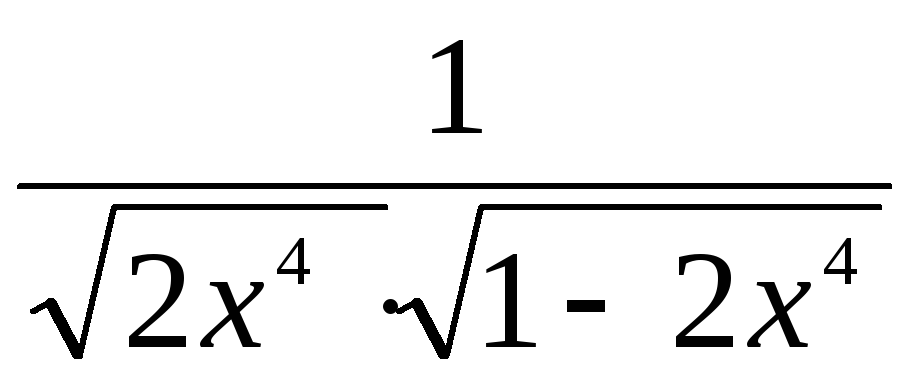
В.
Г.
4. Найти
производную функции 
А.
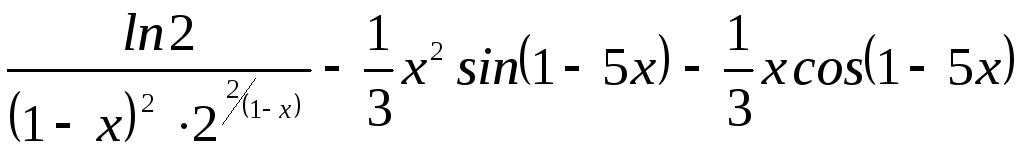
Б.
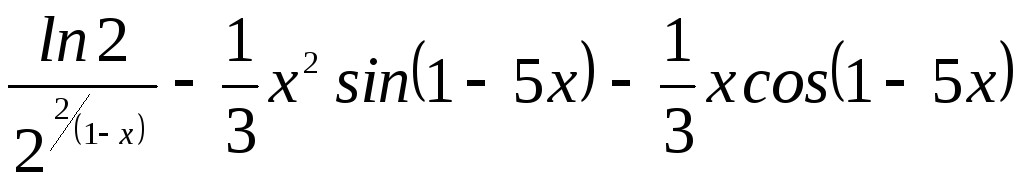
В.
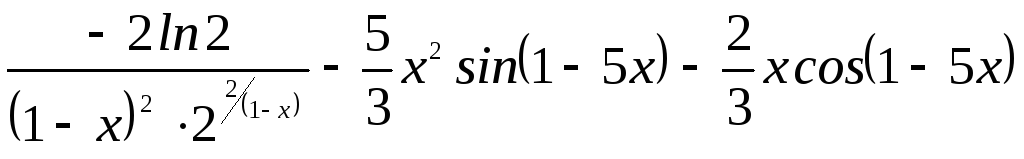
Г.
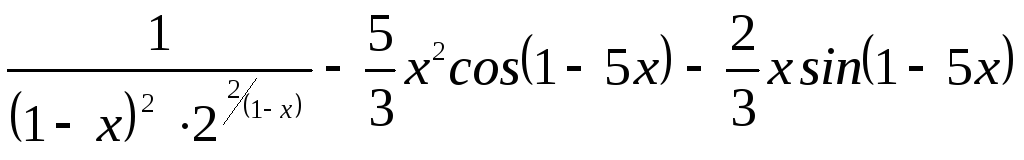
5.
Функция
имеет минимум в точке с координатами
А. (0; 5)
Б. (1; 6)
В. (2; 1)
Г. (3;-22)
6.
Наклонная асимптота для графика функции
имеет вид
А. у = 5
Б. у = –5
В. у = 3
Г. у = –3
7. Выражение
вида
для функцииz
= 3x
- 4xy
+ 2y
+ 6x
+ 4y
+ 7 является
А.
Б
В.
Г.
8. Для
функции
найти значение частной производной пох
в точке
А. -3
Б. -16
В. 16
Г. -8
9.
Найти
для
функции
А.
Б.
В.
Г.
10.
Для функции
найти значение
смешанной производной в точке А (–1,
1).
А. 2
Б. –18
В. –11
Г. 12