
Контрольная по математике
.doc
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ «НИНХ»
Институт________________________________________________
Кафедра________________________________________________
КОНТРОЛЬНАЯ РАБОТА
Учебная дисциплина :________Высшая математика_______________
Номер варианта контрольной работы:__6___
Наименование направления (специальности, профиля подготов-
ки): __
Ф.И.О студента:_____Фомина Ирина валерьевна_________________
Номер группы:_________________МОПО21Н____________________
Номер зачетной книжки___________123726_____________________
Дата регистрации контрольной работы кафедрой_________________
Проверил:__________________________________________________
(Ф.И.О.)
Оценочное заключение:
Новосибирск 2012
Вариант 6
Задача 1.
Дан треугольник АВС: А (2;0), В( -1;4), С (-4;3). Найти:
-
длину стороны АВ;
-
внутренний угол А с точностью до градуса;
-
уравнение и длину высоты, опущенной из вершины С;
-
точку пересечения высот;
-
уравнение медианы, проведенной через вершину С;
-
систему линейных неравенств, определяющих треугольник АВС;
-
Сделать чертеж
Решение.
-
Вычисляем длину стороны АВ: АВ =
 =
= =
5.
=
5. -
Угол — это угол между векторами
 и
и
 .
Координаты этих векторов:
.
Координаты этих векторов:
![]() = (-1 – 2, 4 – 0) = (-3,
4);
= (-1 – 2, 4 – 0) = (-3,
4);
![]() = (-4 – 2, 3 – 0) = (-6, 3).
= (-4 – 2, 3 – 0) = (-6, 3).
Следовательно:
cos
=![]()
По таблице косинусов находим значение угла в радианах: =26,340.
-
Высота СN ортогональна стороне AB. Поскольку сторона AB проходит через две заданные точки и не параллельна осям координат, то она имеет уравнение:
 ;
;
3y+4x-8=0
Расстояние от точки С(-4; 3) до прямой АВ 3y+4x-8=0
![]()
![]()
-
Известно, что высоты треугольника пересекаются в одной точке. Уравнение CN найдено. Аналогично выведем формулу высоты BD, проходящей через точку B перпендикулярна вектору AC (-6;3)
-6(х+1)+3(у-4)=0;
6х-3у+18=0
![]()
отсюда x = 0, y = 6. Таким образом, точка пересечения высот имеет координаты (0, 6).
5. Чтобы получить уравнение медианы CD, определим координаты точки D, являющейся серединой стороны AB. Имеем:
x
0 =
![]() = 0,5; y
0 =
= 0,5; y
0 =
![]() =+2.
=+2.
![]() или 4,5y+x+9,5=0
или 4,5y+x+9,5=0
6. Найдем систему
линейных неравенств, определяющих
треугольник АВС. В пп. 3 и 4 были получены
уравнения сторон АВ и ВС. Сторона АС
имеет уравнение![]() или
2y+x-2=
0.
или
2y+x-2=
0.
Подставим в уравнения прямых, проведенных через две точки, третью.

В результате вычислений получаем:

Следовательно, система, определяющая треугольник имеет вид:
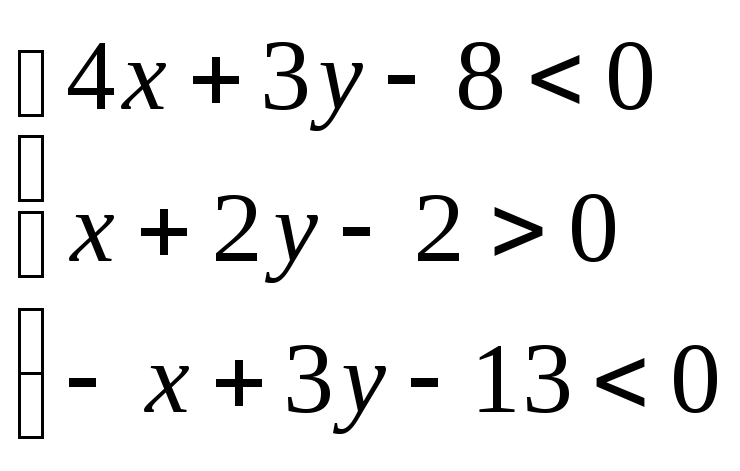
Чертеж:

Задача 2.
Даны векторы:
![]() =
(0;-1;0;2);
=
(0;-1;0;2);
![]() =
(1;-2;2;1);
=
(1;-2;2;1);
![]() =
(-1;1;3;1);
=
(-1;1;3;1);
![]() =
(-2;-1;1;0);
=
(-2;-1;1;0);
![]() =
(-5;-1;0;1). Показать, что векторы
=
(-5;-1;0;1). Показать, что векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() образуют базис четырехмерного векторного
пространства R
(4) и найти
координаты вектора
образуют базис четырехмерного векторного
пространства R
(4) и найти
координаты вектора
![]() в этом базисе.
в этом базисе.
Решение.
Составим определитель из координат
векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() и вычислим его :
и вычислим его :

Прибавим ко третьему столбцу второй, затем к четвертому второй умноженный на 2.

Разложим определитель по первой строке, а затем применим правило треугольников.

Так как
0, то векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() образуют базис, и вектор
образуют базис, и вектор
![]() может
быть разложен по векторам базиса. Пусть
это разложение имеет вид:
может
быть разложен по векторам базиса. Пусть
это разложение имеет вид:
![]()
Для нахождения коэффициентов разложения, используя линейные операции над векторами и условие равенства векторов, перейдем от векторного уравнения к следующей системе линейных уравнений:

Решение системы найдем по формулам Крамера:
x
1 =
![]() ;
x
2 =
;
x
2 =
![]() ;
x
3 =
;
x
3 =
![]() ;
x
4 =
;
x
4 =
![]() ,
,
где определитель системы = -40.
Вычислим далее аналогично:

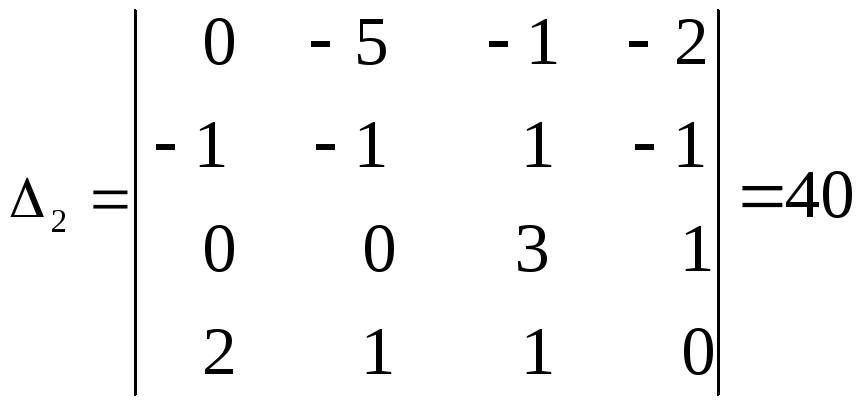


Тогда координаты
вектора
![]() в
базисе
в
базисе
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
x
1 =
![]() ;
x
2 =
;
x
2 =
![]() ;
x
3 =
;
x
3 =
![]() ;
x
4 =
;
x
4 =
![]() ,
,
а разложение
вектора
![]() по базису
по базису
![]() ,
,
![]() ,
,
![]() ,
,
![]() имеет вид:
имеет вид:
![]()
Задача 3.

![]()
y’=![]()

Задача 4.
![]()
-
Функция f (x)
 определена при всех x
(– ;
2)
определена при всех x
(– ;
2) (2;
).
(2;
). -
Поскольку f (– x) f (x) и f (– x) – f (x), то функция не является ни четной, ни нечетной. Следовательно, ее график не симметричен ни относительно оси Oy, ни относительно начала координат.
-
f (x) непериодическая.
-
Вертикальная асимптота

Горизонтальная асимптота.


f (x) имеет вертикальную асимптоту х=2, и горизонтальную у=х+1.
-
Найдем точки пересечения графика с осями координат. Поскольку функция f (x) определена в точке x = 0, то ее график пересекает ось Oy и Ox.
точки пересечения с осями координат при y=0
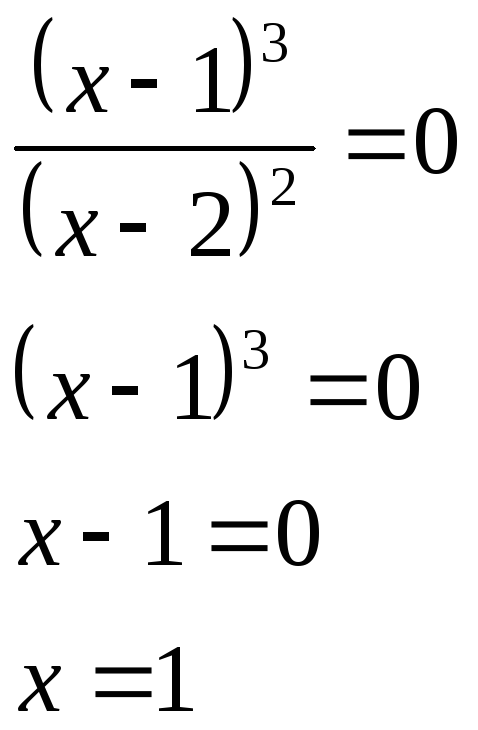
При х=0
![]()
-
Исследуем функцию на возрастание, убывание, экстремумы.

х=2 – стационарная точка первого рода.
![]()
![]()
-
Исследуем функцию на выпуклость, вогнутость, точки перегиба.
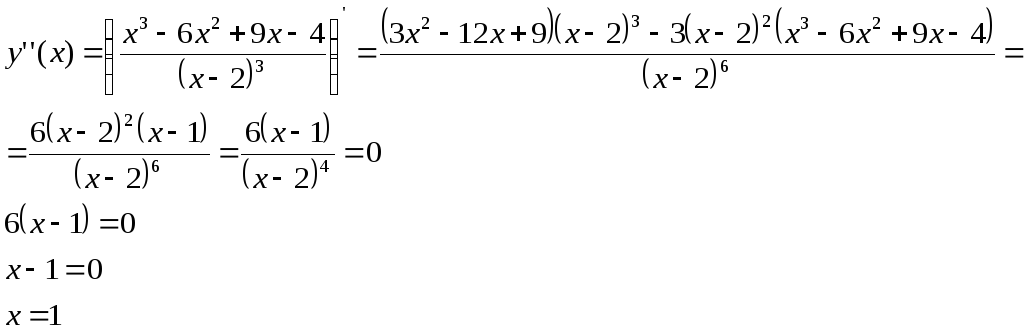
х=2 – стационарная точка первого рода.

![]()
x=1 точка перегиба.

Задача 5.
А)
![]()
Проверка
![]()
Б)

Проверка
![]()
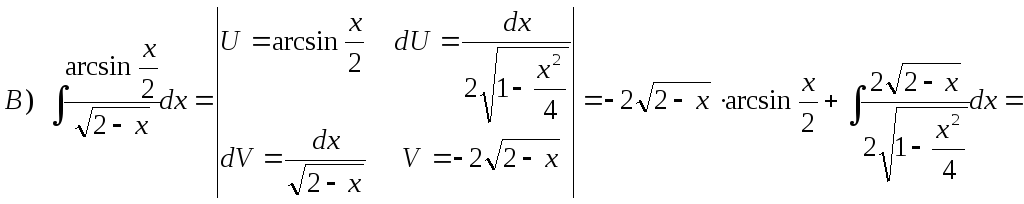
![]()
![]()
проверка

Г)![]()


Задача 6.
Вычислить площадь фигуры, ограниченной графиками функций:
f1(x)=![]()
f2(x)=![]()

![]()
чертеж:

ОСНОВНАЯ ЛИТЕРАТУРА
1. Шипачев В.С. Высшая математика. М: Высшая школа,1998.
2. Сборник задач по математике (для ВТУЗов): линейная алгебра и основы математического анализа / под ред. А.В. Ефимова, Б.П. Демидовича. М: Наука, 1986.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
3. Владимиров Ю.Н. Множества, отображения, функции: учеб. метод. пособие. Новосибирск: НГАЭиУ, 2001.
4. Владимиров Ю.Н. Аналитическая геометрия: краткий справочник. Новосибирск: НГАЭиУ, 2001.
5. Владимиров Ю.Н. Линейная алгебра: краткий справочник. Новосибирск: НГАЭиУ, 2001.
6. Владимиров Ю.Н. Математический анализ функций одной вещественной переменной: краткий справочник. Новосибирск: Сатрен, 1998.
7. Владимиров Ю.Н. Математический анализ функций нескольких веществен-ных переменных: учеб. пособие. Новосибирск: НГАЭиУ, 2004.
8. Владимиров Ю.Н., Гвоздев С.Е., Каленкович Е.Е. и др. Высшая математика: учебно-методический комплекс (для заочной формы обучения). Новосибирск: НГУЭУ, 2005.
9. Каленкович Е.Е. Аналитическая геометрия. Индивидуальное расчетно-графические задание и методические указания по его выполнению. Новосибирск: НГАЭиУ, 1999.
10. Каленкович Е.Е. Интегралы. Индивидуальное расчетно-графическое задание и методические указания по его выполнению. Новосибирск: НГАЭиУ, 2000.
11. Колодко Л.С. Линейная алгебра. Индивидуальное расчетно-графическое задание и методические указания по его выполнению. Новосибирск: НГАЭиУ , 2000.
12. Чиркунов Ю.А. Исследование функций и построение их графиков. Индивидуальное расчетно-графическое задание и методические указания по его выполнению. Новосибирск: НГАЭиУ, 2000.
