Задача 3

Проверка моделей на автокорреляцию и мультиколлинеарность.

1. Для регрессионных моделей:

и

с помощью критерия Дарбина – Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости α=0,05.

2. Для регрессионной модели

проверим наличие или отсутствие мультиколлинеарности, используем:

а) парный коэффициент корреляции (приближённо);

б) критерий «хи - квадрат» χ² на уровне значимости α=0,05.

Решение

1. Для регрессионных моделей

и

с помощью критерия Дарбина – Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости α=0,05.

Статистика Дарбина – Уотсона имеет вид

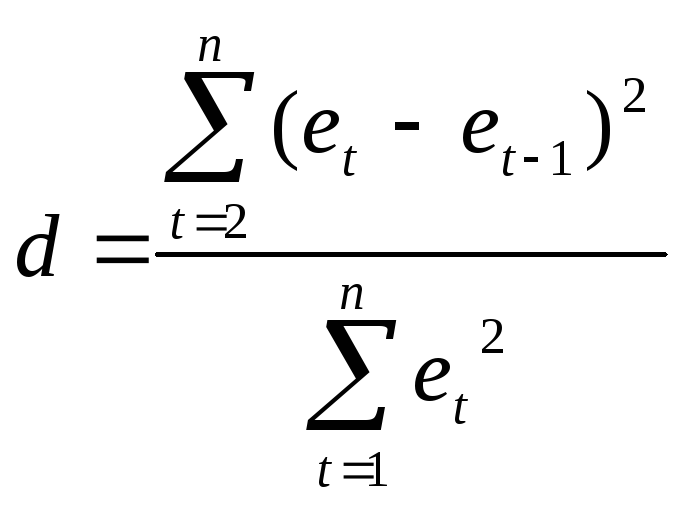
_{Таблица 10.}

Проверим наличие или отсутствие автокорреляции для регрессионной модели

i
	ei	(ei-ei-1)2	ei	(ei-ei-1)2
1	-84,728		40175,83	1614097316
2	-78,912	7178,833984	30794,83	88003161
3	-94,01	33,825856	38759,83	63441225
4	-79,188	227,949604	40765,83	4024036
5	-72,578	219,691684	42476,83	2927521
6	-83,978	43,6921	50146,83	58828900
7	-102,86	129,96	59173,83	81486729
8	-95,634	356,529924	58701,83	222784
9	-57,452	52,215076	60943,83	5026564
10	-76,064	1457,865124	59999,83	891136
11	-118,144	346,406544	71209,83	125664100
12	-138,388	1770,7264	71209,83	0
13	-109,662	409,819536	624358,96	1614097316
14	-64,41	825,183076	40175,83	88003161
15	-124,59	2047,743504	30794,83	63441225
16	-73,864	3621,6324	38759,83	4024036
Итого:	-1454,462	2573,127076	40765,83	2044613472

а)

Получаем

В задаче число наблюдений n=16, число объясняющих переменных m=2.

По таблице находим d₁=0,982; d_u=1,539. В нашем случае условие не выполняется d₁<d<4-d_u, поэтому гипотеза об отсутствии автокорреляции отклоняется.

б)

Получаем

В задаче число наблюдений n=12, число объясняющих переменных m=1.

Согласно теории, d – статистика Дарбина – Уотсона определена для объёмов выборки не менее 15, следовательно, в данном случае применение этой статистики не совсем корректно. Примем n=15, тогда при одной объясняющей переменной m=1 получим:

По таблице находим d₁=0,077; d_u=1,361. В нашем случае не выполняется условие d_u<d<4-d_u, поэтому гипотеза об отсутствии автокорреляции не принимается.

2. Для регрессионной модели

проверим наличие или отсутствие мультиколлинеарности, используем:

а) парный коэффициент корреляции (приближённо);

- уравнение регрессии.

Находим коэффициент парной корреляции между объясняющими переменными, для вычислений воспользуемся Excel (статистическая функция КОРРЕЛ), получаем:

Вычисляем t-статистику:

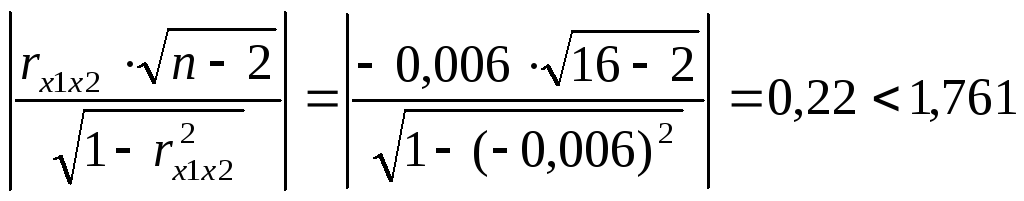- можно говорить, что коэффициенты не коррелируют между собой, следовательно, мультиколлинеарность отсутствует.

б) критерий «хи - квадрат» χ² на уровне значимости α=0,05.

Рассчитаем определитель матрицы коэффициентов парной корреляции:

По формуле получаем:

Табличное значение статистики равно: χ_табл²=3,565

Так как χ_факт²=3,35 меньше χ_табл²=3,565, то можно сделать окончательный вывод об отсутствии мультиколлинеарности.