
- •Теория вероятностей случайные события Основные понятия
- •Операции над событиями
- •Вероятность появления только одного события
- •Формула полной вероятности.
- •Формула Байеса (формула гипотез)
- •Повторение испытаний Формула Бернулли
- •Наивероятнейшее число появлений события в независимых испытаниях
- •Локальная теорема Муавра-Лапласа
- •Интегральная теорема Лапласа
- •Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
- •Формула Пуассона
- •Случайные величины
- •Закон распределения дискретной случайной величины
- •Биноминальное распределение
- •Распределение Пуассона
- •Числовые характеристики дискретных случайных величин
- •Свойства математического ожидания
- •Вычисление дисперсии
- •Свойства дисперсии
- •Среднее квадратическое отклонение
- •Функция распределения
- •Свойства функции распределения
- •Плотность распределения
- •Свойства плотности распределения
- •Числовые характеристики непрерывных случайных величин
- •Законы распределения непрерывных случайных величин
- •Равномерное распределение
- •Показательное распределение
- •Нормальный закон распределения
- •Правило трех
Локальная теорема Муавра-Лапласа
Теорема.
(Локальная теорема Муавра-Лапласа).
Если
вероятность
![]() появления события
появления события![]() в каждом испытании постоянна и отлична
от нуля и единицы, то
в каждом испытании постоянна и отлична
от нуля и единицы, то![]() того, что событие
того, что событие![]() в
в![]() независимых испытаниях появится ровно
независимых испытаниях появится ровно![]() раз, приближенно равна (чем больше
раз, приближенно равна (чем больше![]() ,
тем точнее) :
,
тем точнее) :
![]() ,
где
,
где
![]() - функция Гаусса
- функция Гаусса
Значения
![]() находим
по таблице, при
находим
по таблице, при![]() .
.
Учитываем
,что функция
![]() четная, то есть
четная, то есть![]() .
.
Пример
9. Найти
вероятность того, что событие
![]() (переключение передач) наступит 70 раз
на 243 – километровой трассе, если
вероятность переключения на каждом
километре равна 0,25.
(переключение передач) наступит 70 раз
на 243 – километровой трассе, если
вероятность переключения на каждом
километре равна 0,25.
¦
![]() ,
,![]() ,
,![]() ,
,![]() .
.
1)
![]() .
.
2)
![]()
3)
![]() .
.
Интегральная теорема Лапласа
Пусть
производится
![]() независимых испытаний, в каждом из
которых вероятность появления события
независимых испытаний, в каждом из
которых вероятность появления события![]() равна
равна![]() .
Чтобы вычислить вероятность
.
Чтобы вычислить вероятность![]() ,
того, что событие
,
того, что событие![]() появится не менее
появится не менее![]() не более
не более![]() раз, (
раз, (![]() ),
используем интегральную теорему Лапласа.
),
используем интегральную теорему Лапласа.
Теорема
7. (Интегральная
теорема Муавра-Лапласа).
Если вероятность события
![]() в каждом испытании постоянна и отлична
от нуля и единице, то вероятность
в каждом испытании постоянна и отлична
от нуля и единице, то вероятность![]() того, что событие
того, что событие![]() появится в
появится в![]() испытаниях от
испытаниях от![]() до
до![]() раз, приближенно равна определенному
интегралу:
раз, приближенно равна определенному
интегралу:
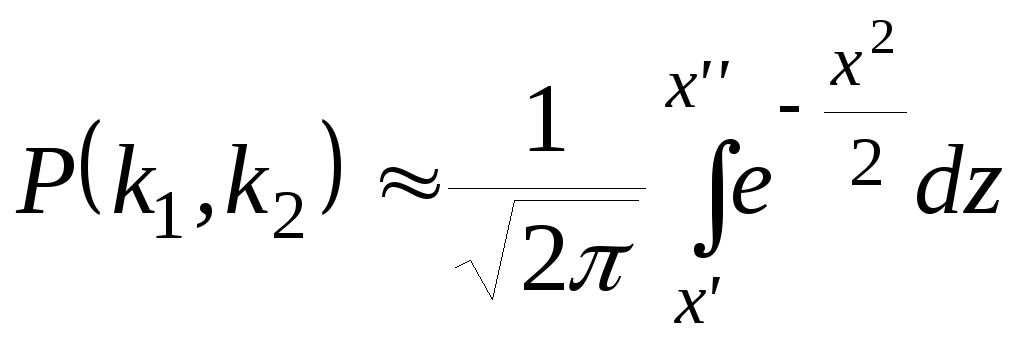 ,
где
,
где
![]() ,
,![]()
Так
как
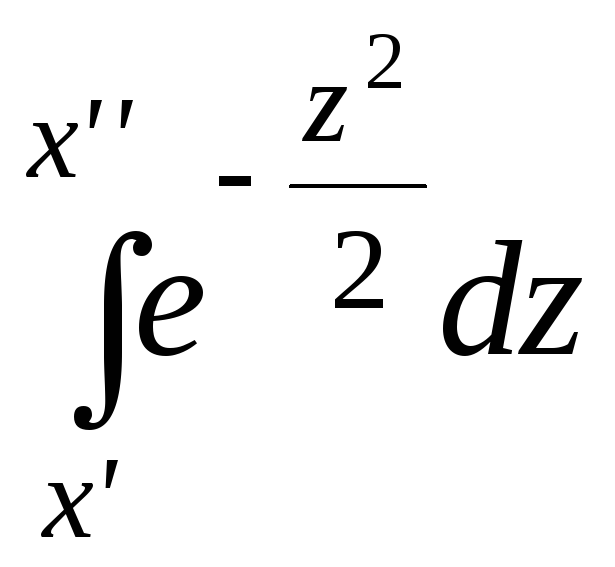 не выражается через элементарные
функции, то его значение находим в
таблице значений функции Лапласа
не выражается через элементарные
функции, то его значение находим в
таблице значений функции Лапласа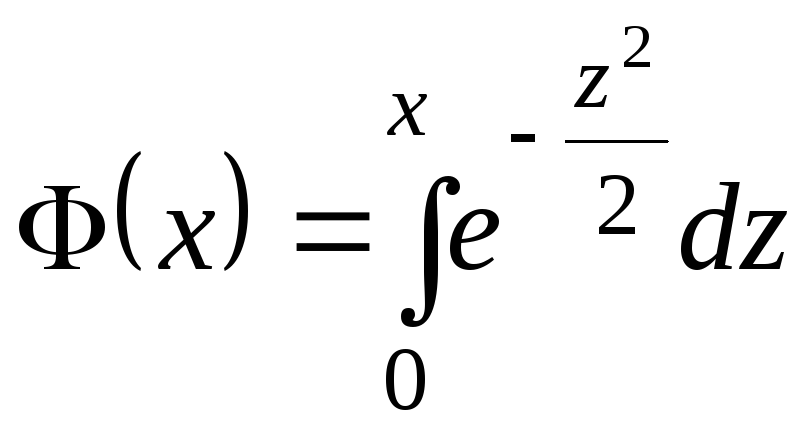 .
.
Учитываем,
что функция
![]() нечетная, то есть
нечетная, то есть![]() .
.
(для
![]() принимаем
принимаем![]() ).
).
Таким образом,
![]() .¢
.¢
Пример
10 . Вероятность
выпуска нестандартной лампы
![]() .
Чему равна вероятность того, что в партии
из 2000 ламп число стандартных не менее
1790 штук.
.
Чему равна вероятность того, что в партии
из 2000 ламп число стандартных не менее
1790 штук.
¦
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]()
![]() .
.
Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
С
помощью функции Лапласа можно найти
вероятность отклонения относительной
частоты
![]() от вероятности
от вероятности![]() в
в![]() независимых испытаниях. Имеет место
формула:
независимых испытаниях. Имеет место
формула:
![]() ,
,
где
![]() - некоторое число.
- некоторое число.
Пример 11. Проверкой качества радиоламп установлено, что 95% из них служит не менее гарантируемого срока. Определить вероятность того, что в партии из 500 ламп, доля ламп, со сроком службы менее гарантируемого срока, будет отличаться от вероятности изготовления не более, чем на 0,02.
¦
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() .
.
Пример 12. Вероятность допущения дефекта при производстве механизмов равна 0,4. Случайным образом отбирается 500 механизмов. Установить величину наибольшего отклонения изготовленных механизмов с дефектами от вероятности 0,4, которую модно гарантировать с вероятностью 0,9973.
¦
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
По
таблице для
![]() находим, что
находим, что
![]() ,
откуда
,
откуда![]() .
.
Формула Пуассона
Если
![]() ,
а вероятность появления события
,
а вероятность появления события
![]() равна
равна![]() ,
так, что
,
так, что![]() остается постоянным и
остается постоянным и![]() ,
то вероятность
,
то вероятность
![]() вычисляем, используя формулу Пуассона:
вычисляем, используя формулу Пуассона:
![]()
Пример 13 . Некоторое электронное устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 часа работы устройства равна 0,004. Какова вероятность того, что за 1000 часов работы устройства придется 5 раз менять микросхему.
¦
![]() ,
,![]() .
.
![]() .
.
По
формуле Пуассона:
![]() .
.
Случайные величины
Выше рассматривались случайные события, являющиеся качественной характеристикой случайного результата опыта. Для получения количественной характеристики вводится понятие случайной величины.
Определение. Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Случайные величины можно разделить на две категории.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
