
- •Федеральное агентство по здравоохранению и социальному развитию
- •I. Материалы ко второму этапу экзамена.
- •Тема №1:«дифференциальное и интегральное исчисления»
- •1. Если производные двух функций тождественно равны, то сами функции
- •26. Если f(X) является одной из первообразных для данной функции f(X), то самое общее выражение, для первообразной имеет вид
- •3. Уравнение, в которое неизвестная функция входит под знаком производной или дифференциала, классифицируется как
- •5. Дифференциальное уравнение относится к
- •6. Особым решением обыкновенного дифференциального уравнения первого порядка является ….
- •7. Общим решением дифференциального уравнения будет
- •11. Уравнение:является
- •16. Случайная величина х дискретного типа принимает два значения 0 и 1 с равными вероятностями. Определите вероятность того, что она примет значение 0
- •46. Дисперсия случайной величины х, имеющей равномерное распределение на отрезке [1, 9] равна
- •13. Задана функция плотности случайной величины, распределенной по нормальному закону:
- •25. Задана функция плотности вероятности случайной величины, распределенной по нормальному закону:
- •26. Статистические данные свидетельствуют о том, что вероятность рождения мальчика равна 0,516. Определите вероятность того, что новорожденный ребёнок окажется девочкой.
- •33. Случайная величина принимает шесть значений: 0, 1, 2, 3, 4, 5 с равными вероятностями. Определите математическое ожидание.
- •50. Применяемый метод лечения приводит к выздоровлению в 90% случаев. Определите вероятность того, что из 5 больных поправятся не менее 4.
- •51. Применяемый метод лечения приводит к выздоровлению в 80% случаев. Определите вероятность того, что из 5 больных поправятся 4.
- •61. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берут на пробу 2 дм3 воздуха. Найдите вероятность того, что в пробе будет обнаружен хотя бы один микроб.
- •Тема №3. «Теория вероятностей и мат.Статистика»
- •Производные и дифференциалы.
- •Частные производные. Применение дифференциального исчисления в теории ошибок измерений.
- •Скалярное поле. Производные по направлению. Градиент.
- •Интегралы. Неопределённые интегралы.
- •Определённые интегралы.
- •Дифференциальные уравнения.
- •Теория вероятностей и математическая статистика.
- •Справочные материалы
- •Оглавление
Тема №3. «Теория вероятностей и мат.Статистика»
|
№ № |
ответы |
№ № |
ответы |
№ № |
ответы |
№ № |
ответы |
№ № |
ответы |
|
1. |
2 |
11. |
3 |
21. |
4 |
31. |
4 |
41. |
2 |
|
2. |
1 |
12. |
2 |
22. |
1 |
32. |
5 |
42. |
3 |
|
3. |
3 |
13. |
2 |
23. |
3 |
33. |
4 |
43. |
4 |
|
4. |
3 |
14. |
1 |
24. |
4 |
34. |
1 |
44. |
5 |
|
5. |
2 |
15. |
1 |
25. |
4 |
35. |
2 |
45. |
2 |
|
6. |
4 |
16. |
2 |
26. |
5 |
36. |
1 |
46. |
4 |
|
7. |
3 |
17. |
3 |
27. |
1 |
37. |
1 |
47. |
1 |
|
8. |
5 |
18. |
3 |
28. |
5 |
38. |
5 |
48. |
1 |
|
9. |
2 |
19. |
3 |
29. |
5 |
39. |
1 |
49. |
2 |
|
10. |
1 |
20. |
3 |
30. |
3 |
40. |
1 |
50. |
3 |
Производные и дифференциалы.
1.1).
Идентифицируем функцию как алгебраическую
сумму. «Производная от суммы равна
сумме производных».2). Представим функцию
в виде степеней аргумента х:
![]() .
.
3).
Вспомним подходящие формулы
дифференцирования y
= xn,y’=
nxn-1.
4).
Применим формулы к заданной функции![]() 5).
Сформулируем окончательный результат:
5).
Сформулируем окончательный результат:![]()
2.
Идентифицируем функцию как алгебраическую
сумму. «Дифференциал от суммы равен
сумме дифференциалов»,т.е.:![]() .
.
Вспомним
подходящие формулы дифференцирования:
y
= xny’=
nxn-1;
y
= sinxy’=
-cosx.Применим
формулы к заданной функции:![]()
Сформулируем окончательный результат:
![]()
3.1). Идентифицируем функцию как
произведение элементарных функций.
Вспомним правило получения производной
от произведения элементарных функций:y=u(x)
· v(x);y’=u´(x)
·v(x) +v´u(x)
(x); 2). Представим функцию
в виде удобном для дифференцирования:
![]() .3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
-sinx. 4). Применим формулы
к заданной функции:
.3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
-sinx. 4). Применим формулы
к заданной функции:![]() .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:![]()
4.1). Идентифицируем функцию как произведение
элементарных функций. Вспомните правило
получения производной от произведения
элементарных функций:y=u(x) · v(x);y’=u´(x)
·v(x) +v´u(x)
(x); 2). Представим функцию
в виде удобном для дифференцирования
:
![]() .3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
=-sinx. 4). Применим
формулы к заданной функции:
.3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
=-sinx. 4). Применим
формулы к заданной функции:![]() .5).
Сформулируем окончательный результат:
.5).
Сформулируем окончательный результат:![]()
5.1). Идентифицируем функцию как частное
элементарных функций. Вспомним правило
получения производной от частного
элементарных функций:
![]() .
2). Представим функцию в виде удобном
для дифференцирования:
.
2). Представим функцию в виде удобном
для дифференцирования: ![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1.4).
Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1.4).
Применим формулы к заданной функции: .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:

6.1).
Идентифицируем функцию как частное
элементарных функций. Вспомним правило
получения дифференциала от частного
элементарных функций:
![]() . 2). Представим функцию в виде удобном
для дифференцирования:
. 2). Представим функцию в виде удобном
для дифференцирования: ![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
-sinx;y=sinxy’=cosx. 4). Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=cosxy’=
-sinx;y=sinxy’=cosx. 4). Применим формулы к заданной функции: .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:

7.1). Идентифицируем функцию как произведение
элементарных функций. Вспомнм правило
получения производной от произведения
элементарных функций:y=u(x) · v(x);y’=u´(x)
·v(x) +v´u(x)
(x);2). Представим функцию
в виде удобном для дифференцирования:
![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=lnxy’=
1/x. 4). Применим формулы к
заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=lnxy’=
1/x. 4). Применим формулы к
заданной функции:![]() .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:
![]()
8.1).
Идентифицируем функцию как произведение
элементарных функций. Вспомним правило
получения производной от произведения
элементарных функций:y=u(x) · v(x);y’=u´(x)
·v(x) +v´u(x)
(x); 2). Представим функцию
в виде удобном для дифференцирования:
![]() .3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=sinxy’=cosx;y=exy’=ex4).
Применим формулы к заданной функции:
.3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=sinxy’=cosx;y=exy’=ex4).
Применим формулы к заданной функции:![]() .5).
Сформулируем окончательный результат,
воспользовавшись определением
дифференциала:
.5).
Сформулируем окончательный результат,
воспользовавшись определением
дифференциала:
9.1).
Идентифицируем функцию как частное от
деления алгебраической суммы элементарных
функций на произведение элементарных
функций. Вспомним правила получения
производной от произведения элементарных
функций:y=u(x)
· v(x);y’=u´(x)
·v(x) +v´u(x)
(x);и
![]() 2). Представим функцию в виде удобном
для дифференцирования:
2). Представим функцию в виде удобном
для дифференцирования: ![]() 3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=sinxy’=cosx;y=lnxy’= 1/x. 4). Применим формулы
к заданной функции:
3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y=xny’=nxn-1;y=sinxy’=cosx;y=lnxy’= 1/x. 4). Применим формулы
к заданной функции: .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:
10.1).
Идентифицируем функцию как частное от
деления произведения элементарных
функций на произведение постоянной и
элементарной функции. Вспомним правила
получения производной от произведения
элементарных функций и от частного:y=u(x) · v(x);y’=u´(x)
·v(x) +v´u(x)
(x); и
![]() .
2). Представим функцию в виде удобном
для дифференцирования:
.
2). Представим функцию в виде удобном
для дифференцирования:
3).
Вспомним подходящие для данного случая
основные формулы дифференцирования: y
= xny’=
nxn-1;
y
= ctgxy’=
-1 /sin2x;
y
= lgxy’
= 1/(x
· ln10).4).
Применим формулы к заданной функции:
 .
5). Сформулируем окончательный результат
вспомнив, что дифференциал функции:dy
= y’dx:
.
5). Сформулируем окончательный результат
вспомнив, что дифференциал функции:dy
= y’dx:

11.
1). Идентифицируем функцию как
частное от деления произведения
элементарных функций на алгебраическую
сумму элементарных функций. Вспомним
правила получения производной от
алгебраической суммы, от произведения
элементарных функций и от частного
элементарных функций:y=u(x) + v(x);y’=u´(x)
+v´(x);y=u(x) ·v(x);y’=u´(x)
·v(x)
+v´(x)u(x);и
![]() .
.
2).
Представим функцию в виде удобном для
дифференцирования: .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y
= xny’=
nxn-1;
y
= sinxy’=
cosx;
y
= cosxy’
= - sinx.4).
Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y
= xny’=
nxn-1;
y
= sinxy’=
cosx;
y
= cosxy’
= - sinx.4).
Применим формулы к заданной функции:
 5).Сформулируемокончательный
результат:
5).Сформулируемокончательный
результат:
12.1).
Идентифицируем функцию как частное от
деления алгебраической суммы элементарных
функций на алгебраическую сумму
элементарных функций. Вспомним правила
получения производной от алгебраической
суммы элементарных функций:
 иy=u(x)
+ v(x);y’=u(x)
+v´(x).
иy=u(x)
+ v(x);y’=u(x)
+v´(x).
2).
Представим функцию в виде удобном для
дифференцирования:
 .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y
= xny’=
nxn-1
. 4).
Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y
= xny’=
nxn-1
. 4).
Применим формулы к заданной функции:
 5). Сформулируем окончательный ответ,
воспользовавшись определением
дифференциала.
5). Сформулируем окончательный ответ,
воспользовавшись определением
дифференциала.
Ответ:
dy
= y’dx;

13.1).
Идентифицируем функцию как алгебраическую
сумм у произведений элементарных
функций. Вспомним правила получения
производной от суммы и от произведения
элементарных функций:y=u(x) +v(x);y’=u´(x)
+v´(x);y=u(x) ·v(x);y’=u´(x)
·v(x) +v´u(x)
(x). 2). Представим функцию
в виде удобном для дифференцирования:![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1.
4). Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1.
4). Применим формулы к заданной функции:![]() .
5). Сформулируем окончательный ответ:
.
5). Сформулируем окончательный ответ:![]()
14.1). Идентифицируем функцию как
алгебраическую сумму элементарных
функций. Вспомним правила получения
производной от суммы и от произведения
элементарных функций:y=u(x) +v(x);y’=u´(x)
+v´(x); 2).
Представим функцию в виде удобном для
дифференцирования:![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=tgxy’= 1/cos2x.
4). Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1;y=tgxy’= 1/cos2x.
4). Применим формулы к заданной функции:![]() .
5). Сформулируем окончательный результат,
вспомнив определение дифференциала:
.
5). Сформулируем окончательный результат,
вспомнив определение дифференциала:![]()
15.1).
Идентифицируем функцию как произведение
элементарных функций. Вспомним правило
получения производной от произведения
элементарных функций:y=u(x) · v(x);y’=u´(x)
·v(x)
+v´(x)u(x);
2). Представим функцию в виде удобном
для дифференцирования: ![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=ctgxy’=
- 1/sinx;y=exy’=ex.
4). Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=ctgxy’=
- 1/sinx;y=exy’=ex.
4). Применим формулы к заданной функции:![]() 5).
Сформулируем окончательный результат:
5).
Сформулируем окончательный результат:
![]()
16.1).
Идентифицируем функцию как частное
элементарных функций. Вспомните правило
получения дифференциала от частного
элементарных функций:
![]() . 2). Представим функцию в виде удобном
для дифференцирования:
. 2). Представим функцию в виде удобном
для дифференцирования: ![]() .
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1. 4). Применим формулы к заданной функции:
.
3). Вспомним подходящие для данного
случая основные формулы дифференцирования:y=xny’=nxn-1. 4). Применим формулы к заданной функции: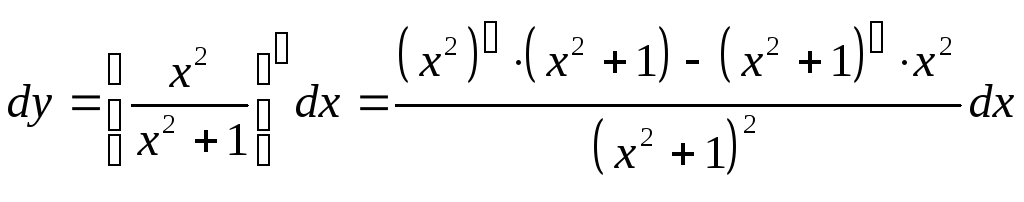 .
5). Сформулируем окончательный результат:
.
5). Сформулируем окончательный результат:

17![]()
18.![]() .
.
19.![]() ;
;
 .
.
20.1). Идентифицируем функцию как частное от деления произведения элементарных функций на произведение постоянной и элементарной функции. Вспомним правила получения производной от произведения элементарных функций и от частного:y=u(x) ·v(x);y’=u´(x) ·v(x) +v´u(x) (x);
и![]() ; f(x) = a · y(x) = a · y’(x).
2).
Представим функцию в виде удобном для
дифференцирования:
; f(x) = a · y(x) = a · y’(x).
2).
Представим функцию в виде удобном для
дифференцирования:
![]() 3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y
= xny’=
nxn-1;
y
= cosxy’=
- sinx;
y
= lnxy’
= 1/x
3).
Вспомним подходящие для данного случая
основные формулы дифференцирования:y
= xny’=
nxn-1;
y
= cosxy’=
- sinx;
y
= lnxy’
= 1/x
4). Применим формулы
к заданной функции:

5).
Сформулируемответ, вспомнив, что
дифференциал функции: dy
= y’dx:
![]()
21.![]() .
.
22.![]()
23.![]() .
.
24.![]()
25. Представим
функцию в виде:![]() где
где
![]() .По
правилу нахождения производной сложной
функции:
.По
правилу нахождения производной сложной
функции:![]() или
или![]() .
.
26.
1). Скорость изменения функции (в данном
случае функция - сила электрического
тока) определяется её производной,
которая, по сформулированному закону,
должна быть наибольшей по величине. 2).
Поскольку требуется построить график,
то следует обратиться к геометрическому
смыслу производной. Геометрически
производная равна тангенсу угла наклона
касательной к оси независимой переменной
- времени. 3). Тангенс будет стремиться
к бесконечности, когда угол стремится
к π/2. 4). Проведём изоклину с максимально
возможным тангенсом наклона. Получаем
перпендикуляр к оси времени в качестве
переднего фронта импульса тока.
27. Рассмотрим амплитуду как функцию частоты вынуждающей силы Ω и обратим внимание на то, что от Ω зависит знаменатель. Следовательно, минимум выражения в знаменателе соответствует максимуму амплитуды.
Рассмотрим
подкоренное выражение в знаменателе
как функцию частоты вынуждающей силы
![]() и проанализируем эту функцию на условия
минимума. Для чего получим выражение
для производной этой функции.
и проанализируем эту функцию на условия
минимума. Для чего получим выражение
для производной этой функции.

Необходимое условие
экстремального значения:
![]() имеет три решения первое очевидно ─
1)
имеет три решения первое очевидно ─
1)![]() ;
второе и третье найдём, решая уравнение:
;
второе и третье найдём, решая уравнение:![]() .
.![]()
![]() 2)
2)
![]() ,
,
3) ![]()
Решение 2) ![]() отбрасываем так, как частота колебаний
не может быть отрицательной. Сформулируем
условие минимума:
отбрасываем так, как частота колебаний
не может быть отрицательной. Сформулируем
условие минимума:

![]()
![]()
Для
![]() ,
учитывая, что при колебаниях,
,
учитывая, что при колебаниях,![]() получаем
получаем
![]() , а это соответствует максимуму знаменателя
формулы:
, а это соответствует максимуму знаменателя
формулы:
При ![]() вторая производная:
вторая производная:
![]()
![]() >
0
>
0
![]() и знаменатель формулы:
и знаменатель формулы: минимален.
минимален.
Следовательно,
резонансной частотой является: ![]() иначе:
иначе:![]() .
.
28. Для определения амплитуды при резонансе подставим найденное значение резонансной частоты (см. задачу 27)
![]() в формулу
в формулу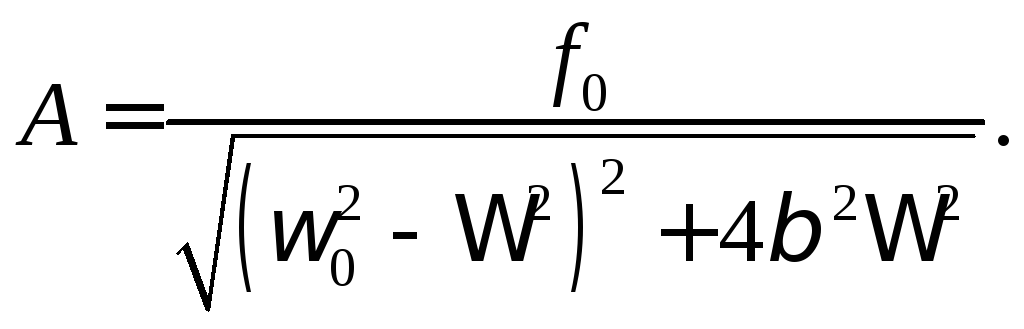

В случае отсутствия
затухания:
![]() и
и![]()
29.
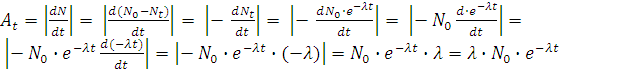 .
.
