4.45. Приведите примеры магнетиков, входящих в состав биологических систем.

4.46. Укажите тип магнетиков, к которому относятся свободные радикалы в биологических системах.

4.47. Определите расстояние от длинного прямого провода с током силы I =5,50 А, с которого начинается «зона безопасности» по отношению к магнитному полю промышленной частоты. За предельно допустимое значение индукции магнитного поля принять стандарт Швеции - 0,2 мкТл.

4.48. В соответствии с теорией Бора в невозбужденном атоме водорода электрон движется вокруг ядра по круговой траектории. Магнитные моменты атомов измеряют в магнетонах Бора. Один магнетон Бора равен μ _B= 9,28 ·10 ^–24 А·м², r = 0,53 ·10^-8 см, v = 2,19 · 10⁶ м/с. Где r - радиус траектории (орбиты), v - скорость электрона на орбите. Определите силу тока, обусловленную орбитальным движением электрона.

4.49. В соответствии с теорией Бора в невозбужденном атоме водорода электрон движется вокруг ядра по круговой траектории. Магнитные моменты атомов измеряют в магнетонах Бора. Один магнетон Бора μ _B= 9,28 ·10 ^–24 А·м², r = 0,53 ·10^-8 см, v = 2,19 · 10⁶ м/с. Где r - радиус траектории (орбиты), v - скорость электрона на орбите. Определите магнитный момент, обусловленный орбитальным движением электрона.

4.50. Круговой виток радиуса r = 3 мм с током силы I = 100 мкА ориентирован так, что его магнитный момент направлен вдоль силовой линии однородного магнитного поля с индукцией B = 40 мТл. Определите работу, которую необходимо совершить, чтобы повернуть виток на угол 120 градусов.

4.51. Круговой виток радиуса r = 2 мм с током силы I= 200 мкА ориентирован так, что его магнитный момент направлен против силовой линии однородного магнитного поля с индукцией B = 50 мТл. Определите работу, которую необходимо совершить, чтобы повернуть виток на угол 30 градусов.

4.52. В однородном магнитном поле свободно с периодом T = 60 с колеблется рамка с током силы I = 0,2 А. Площадь рамки с током S = 10 см², момент инерции J = 0,002 кг·м². Определите магнитную индукцию поля. Максимальный угол отклонения рамки мал.

4.53. В эксперименте были определены значения удельной электрической проводимости тканей головного мозга человека на двух разных частотах электромагнитного поля. При этом были получены данные: 5,06 мСм/см и 5,36 мСм/см. Определите частоту, которой соответствует значение - 5,06 мСм/см. Использованные в эксперименте частоты составляли 50 МГц и 100 МГц.

4.54. Электрическая схема состоит из параллельно соединенных чисто активного сопротивления R = 0,92 кОм и идеальной электрической емкости C = 140 нФ. Определите значение, к которому стремится импеданс схемы, когда частота приложенного к схеме напряжения стремится к бесконечности.

4.55. Электрическая схема состоит из последовательно соединенных чисто активного сопротивления R = 0,77 кОм и идеальной электрической емкости C = 110 нФ. Определите значение, к которому стремится импеданс схемы, когда частота приложенного к схеме напряжения стремится к бесконечности.

4.56. В Вашем распоряжении имеются элементы - модели абсолютных электрических свойств (сопротивления, ёмкости, индуктивности). Соберите их этих элементов эквивалентную схему (схему замещения) электрического импеданса отмирающей биологической ткани.

4.57. При реографии некоторого сосудистого участка, имеющего форму цилиндра с объемом 20,0 мм³, было зарегистрировано уменьшение активной составляющей электрического импеданса на 4 %. Определите конечное значение объема сосудистого участка, которое соответствует зарегистрированному изменению импеданса.

4.58. При реографии некоторого сосудистого участка, имеющего форму цилиндра с объемом 30,0 мм³ , было зарегистрировано увеличение активной составляющей электрического импеданса на 2 %. Определите конечное значение объема сосудистого участка, которое соответствует зарегистрированному изменению импеданса.

4.59. Рассчитайте для живой ткани абсолютную величину тангенса угла между током и напряжением при пропускании через ткань электрического тока низкой частоты 80 Гц, используя для вычислений простейшие эквивалентные схемы. Активное сопротивление ткани составляет 30 кОм, а емкость 4 мкФ.

4.60. Рассчитайте электрический импеданс живой ткани на низкой частоте 40 Гц, используя для вычислений простейшие эквивалентные схемы. Активное сопротивление ткани составляет 40 кОм, а емкость 2 мкФ.

4.61. Рассчитайте для живой ткани абсолютную величину тангенса угла между током и напряжением при пропускании через ткань электрического тока высокой частоты 20 кГц, используя для вычислений простейшие эквивалентные схемы. Активное сопротивление ткани составляет 1 кОм, а емкость 1 нФ.

4.62. Рассчитайте электрический импеданс живой ткани на высокой частоте 100 МГц, используя для вычислений простейшие эквивалентные схемы. Активное сопротивление ткани составляет 10 Ом, а емкость 1 нФ.

4.63. Рассчитайте коэффициент поляризации (коэффициент поляризации Тарусова), для ткани печени после трансплантации органа, используя для вычислений простейшие эквивалентные схемы. Если на частоте зондирующего тока 10 кГц были зарегистрированы значения активной составляющей импеданса R(1) = 0,97 кОм и емкость C(1) = 150 нФ, а на частоте 1 МГц - R(2) = 89 Ом, и емкость C(2) = 23 нФ.

4.64. Оцените жизнеспособность ткани печени после трансплантации органа, если на частоте зондирующего тока 10 кГц были зарегистрированы значения активной составляющей импеданса R(1) = 2,5 кОм и емкость C(1) = 50 нФ, а на частоте 1 МГц - R(2) = 20 Ом, и емкость C(2) = 6 нФ.

4.65. Для тканей межзубного десневого сосочка при остром пульпите рассчитайте электрический импеданс. Используйте эквивалентную схему, состоящую из резистора и конденсатора, присоединённого параллельно резистору. Если на частоте зондирующего тока 1 кГц были зарегистрированы значения активной составляющей импеданса R = 113 кОм и емкость C =11 нФ.

4.66. Для тканей обнаженной пульпы при остром пульпите рассчитайте абсолютную величину угла сдвига фаз между током и напряжением. Используйте эквивалентную схему, состоящую из параллельно соединённых резистора и конденсатора. Если на частоте зондирующего тока 1 кГц были зарегистрированы значения активной составляющей импеданса R = 63 кОм и ёмкости C =5 нФ.

4.67. Определите максимальное значение плотности тока проводимости в однородном проводнике с удельной электрической проводимостью 0,015 См/м, если в нем существует постоянное электрическое поле с напряженностью 50 В/м.

4.68. Определите максимальное значение плотности тока проводимости в однородном проводнике с удельной электрической проводимостью 0,015 См/м, если в нем существует электрическое поле с напряженностью, изменяющейся по закону E = 50 COS(62,8·t) В/м.

4.69. Определите максимальное значение плотности тока смещения в однородном проводнике с удельной электрической проводимостью 0,022 См/м, если в нем существует постоянное электрическое поле с напряженностью 50 В/м.

4.70. Определите максимальное значение плотности тока смещения в однородном проводнике с удельной электрической проводимостью 0,025 См/м и относительной диэлектрической проницаемостью 100 , если в нем существует электрическое поле с напряженностью, изменяющейся по закону E = 90 COS(62,8·t) В/м.

4.71. На поверхность некоторого вещества падает электромагнитная волна с амплитудой напряженности электрического поля равной 700 мВ/м. Определите величину амплитуды напряженности волны на расстоянии от поверхности вещества, равном глубине проникновения.

4.72. На поверхность некоторого вещества падает электромагнитная волна с интенсивностью равной 200 мВт/м². Определите величину интенсивности волны на расстоянии от поверхности вещества, равном глубине проникновения.

4.73. Вещество находится в электрическом поле, напряженность которого изменяется по гармоническому закону с частотой 10 МГц. Удельная электрическая проводимость и относительная диэлектрическая проницаемость вещества на данной частоте составляют γ = 485 См/м и ε_r= 1000. Определите тип электрика, к которому относится вещество при данных обстоятельствах.

4.74. Определите длину волны электромагнитного излучения в веществе с относительной магнитной проницаемостью равной 1 и относительной диэлектрической проницаемостью ε_r = 9 , если частота излучения f = 60 ГГц.

4.75. Определите границу «ближней зоны» для плоской монохроматической электромагнитной волны с частотой f = 20 МГц, излучаемой источником в вакуум.

4.76. Для мышечной ткани экспериментально определенная глубина проникновения электромагнитной волны с частотой 433 МГц составила 3,57 см. Рассчитайте, при прочих равных условиях, глубину проникновения в ткань электромагнитной волны с частотой 5000 МГц.

4.77. Вещество находится в электрическом поле, напряженность которого изменяется по гармоническому закону с частотой 10000 МГц. Удельная электрическая проводимость и относительная диэлектрическая проницаемость вещества на данной частоте составляют γ = 80 См/м и ε_r = 100000. Определите тип электрика, к которому относится вещество при данных обстоятельствах.

РЕШЕНИЯ, УКАЗАНИЯ, ОТВЕТЫ

3. КОЛЕБАНИЯ И ВОЛНЫ, БИОАКУСТИКА.

3.1. Гармонические колебания по закону косинуса происходят в соответствии с формулой:

. Подставим данные из условия задачи в формулу: . Откуда получаем: . И окончательный ответ: .

3.2. Гармонические колебания по закону косинуса происходят в соответствии с формулой:

. Подставим данные из условия задачи в формулу: . Откуда получаем: . И получим окончательный ответ: .

3.3. Из условия ясно, что материальная точка совершает гармонические колебания по закону синуса. Общий вид закона:

. Ускорение получим, дважды продифференцировав смещение по времени.

,

.

Ускорение при гармонических колебаниях изменяется по гармоническому закону с максимальным значением, равным амплитуде ускорения: .

Ответ:.

3.4. Если в колебательной системе происходят гармонические колебания, то частота этих колебаний не зависит от амплитуды колебаний. Таково содержание закона Галилея.

Гармонические колебания – это «малые» колебания, могут происходить с разными, но небольшими амплитудами. Ответ: частота гармонических колебаний осталась неизменной и равна 46 герцам.

3.5. В данном случае мы имеем дело с частным проявлением биений. Биения возникают при сложении однонаправленных гармонических колебаний разных, но близких частот. Для простоты будем считать амплитуды колебаний равными (обозначим их ), круговая частота первого колебания - , второго –, причём. , . Результат сложения колебаний: . Воспользовавшись известной формулой тригонометрии:

и, положив и , получим:. Учитывая, что:

, получим:

. Полученное соотношение допускает следующее формальное истолкование. Произведениемало меняетсяза товремя, за которое произойдёт много колебаний с круговой частотой . На этом основании будем считать амплитудой биений. Но частота изменения абсолютной величины косинуса в два раза больше частоты изменения самого косинуса. Эту удвоенную частоту назовём частотой биений. Применив эти соображения к задаче, получим:

частоту изменений амплитуды результирующего колебания (частоту биений) = (6003-6000) Гц = 3 Гц. Круговая частота биений Ответ: 3 Гц.

3.6. В данном случае мы имеем дело с частным проявлением биений. Биения возникают при сложении однонаправленных гармонических колебаний разных, но близких частот. Для простоты будем считать амплитуды колебаний равными (обозначим их ), круговая частота первого колебания - , второго –, причём . , . Результат сложения колебаний: . Воспользовавшись известной формулой тригонометрии:

и, положив и , получим: . Учитывая, что:,

. Полученное соотношение допускает следующее формальное истолкование. Произведениемало меняетсяза товремя, за которое произойдёт много колебаний с круговой частотой . На этом основании будем считать амплитудой биений. Но период изменения абсолютной величины косинуса в два раза меньше периода изменения самого косинуса. Применив эти соображения к задаче, получим: .

3.7. Для ответа на поставленный вопрос достаточно вспомнить уравнение гармонических колебаний.

далее, разделив на массу,

, и обозначив , получим уравнение динамики гармонического движения в каноническом виде: .

Круговая частота гармонических колебаний связана с периодом однозначно: ..

Ответ:.

3.8. ЭКГ, в лучшем случае, представляет собою график периодически повторяющихся комплексов, т.е. не является синусоидой.

Если допустить правильное чередование комплексов – периодичность, то ЭКГ можно представить в виде гармонического ряда (ряда Фурье). Первая гармоническая составляющая в таком ряду (первая или основная гармоника) будет иметь частоту обратную периоду и численно равную ЧСС в секунду. Вторая гармоника будет иметь вдвое большую частоту. Следовательно: = 1,1 ,

Ответ:

3.9. Для ответа на поставленный вопрос достаточно вспомнить уравнение гармонических колебаний.

далее, разделив на массу,

, и обозначив , получим уравнение динамики гармонического движения в каноническом виде: .

Круговая частота гармонических колебаний однозначно связана с частотой: ..

Ответ: .

3.10. Для ответа на поставленный вопрос достаточно вспомнить уравнение гармонических колебаний.

далее, разделив на массу,

, и обозначив , получим уравнение динамики гармонического движения в каноническом виде: .

,

Ответ:.

3.11. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения потенциальной энергии при гармонических колебаниях.

, где , m.

=

=

Полученное выражение потенциальной энергии

говорит о том, что потенциальная энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда потенциальной энергии равна: .

В нашем случае: частота смещения равна: . Частота изменения потенциальной энергии:

. Ответ: .

3.12. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения кинетической энергии при гармонических колебаниях.

, где.

=

.

Полученное выражение кинетической энергии

говорит о том, что кинетическая энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда кинетической энергии равна: .

В нашем случае: частота смещения равна: . Частота изменения кинетической энергии:

.

Ответ: .

3.13. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения потенциальной энергии при гармонических колебаниях.

, где, m.

=

=

.

Полученное выражение потенциальной энергии

говорит о том, что потенциальная энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда потенциальной энергии равна: .

В нашем случае: частота смещения равна: . Частота изменения потенциальной энергии: . Период колебаний потенциальной энергии:

Ответ: .

3.14. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения кинетической энергии при гармонических колебаниях.

, где .

=

.

Полученное выражение кинетической энергии

говорит о том, что кинетическая энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда кинетической энергии равна: .

В нашем случае: частота смещения равна: . Частота изменения кинетической энергии: . Период колебаний кинетической энергии:

Ответ: .

3.15. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения потенциальной энергии при гармонических колебаниях.

, где , m.

=

=

Полученное выражение потенциальной энергии

говорит о том, что потенциальная энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда потенциальной энергии равна: .

В нашем случае: круговая частота смещения равна: . Круговая частота изменения потенциальной энергии:

. Ответ: .

3.16. По условию задачи гармонические колебания происходят по закону косинуса. Запишем закон гармонических колебаний и получим из него закон изменения кинетической энергии при гармонических колебаниях.

, где .

=

.

Полученное выражение кинетической энергии

говорит о том, что кинетическая энергия при гармонических колебаниях изменяется по гармоническому закону с частотой в два раза большей, чем частота колебаний смещения точки от положения равновесия и амплитуда кинетической энергии равна: .

В нашем случае: круговая частота смещения равна: . Круговая частота изменения кинетической энергии:

.

Ответ: .

3.17. По условию задачи гармонические колебания происходят по закону косинуса. Гармонические колебания происходят в изолированной системе и в случае механических колебаний сумма потенциальной и кинетической энергии в любой момент времени равна полной механической энергии. Полная энергия колебательной системы остаётся постоянной. Запишем закон гармонических колебаний и получим из него закон изменения потенциальной энергии при гармонических колебаниях.

, где , m.

=

=.

Закон изменения кинетической энергии при гармонических колебаниях, происходящих по закону косинуса

(

, где .

Выражение для полной энергии колебаний:

+.

В нашем случае:

.

Ответ: Полная энергия колебательной системы при гармонических колебаниях остаётся постоянной. . ..

3.18. Выражение для полной энергии колебаний:

+ .

Найдём отношение энергий гармонических колебаний для рассматриваемых случаев: . Откуда следует расчётная формула: .

Ответ: = 2

3.19 . По определению . Далее воспользуемся законом изменения амплитуды при затухающих колебаниях

ч.т.д..

3.20. Время, в течение которого произойдут колебаний равно , где период затухающих колебаний. По определению

. Из условия задачи:

или

3.21. Будем предполагать, что имеем дело со случаем, когда в системе наблюдаются затухающие колебания, амплитуда которых экспоненциально убывает со временем по закону: . Пусть – время, за которое произошли n полных колебаний.и. . Откуда: .

Ответ: логарифмический декремент затухания

.

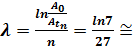
3.22. До предела упрощая ситуацию, будем считать формулу для силы Стокса применимой, хотя скорость шарика при гармонических колебаниях не является постоянной. Сила Стокса - пример диссипативной силы, пропорциональной скорости. Вспомнив дифференциальное уравнение затухающих колебаний: (или, , обозначив , представив в каноническом виде:

убеждаемся, что: . Коэффициент затухания легко находится из времени, за которое амплитуда колебаний уменьшится в «е» раз.

, .

, .

Ответ:.

3.23. Используя формулу амплитуды затухающих колебаний, запишем выражение для отношения амплитуды в начальный момент A₀ к амплитуде в момент времени t(A_t) :Прологарифмируем полученный результат по основаниюe: Запишем формулу для промежутка времениt, используя число полных колебаний n и период колебаний T: t = n · T. Вспомним выражение для логарифмического декремента затухания: Получим расчётную формулу, подставим числовые значения, получим окончательный ответ: