4.56. Решение. Для ответа на поставленный вопрос необходимо располагать данными о дисперсии импеданса живых и отмирающих биологических тканей. Эти данные представлены на рисунке.

Из рисунка следует, что для отмирающей ткани дисперсия импеданса отсутствует. Точно также будет себя вести при изменении частоты идеальное сопротивление (идеальный резистор).

Ответ. Эквивалентная схема (схема замещения) электрического импеданса отмирающей биологической ткани содержит один элемент – идеальное активное сопротивление (резистор).

4.57. Решение. Рассмотрим объём крови с удельным сопротивлением - ρ в виде цилиндра высоты - l и площади поперечного сечения -S. Запишем формулу объёма цилиндра: V = S · l. Получим формулу для относительного изменения объёма цилиндра:

Получим формулу для относительного изменения электрического сопротивления цилиндрического проводника с удельным сопротивлением ρ, длиной lи площадью поперечного сечения –S:

;; считая ρ и постоянными и перейдя к конечным приращениям: .

Сравнив, полученные выражения, получим формулу Кедрова для реографии: . Применим формулу Кедрова к данным из условия задачи и получим окончательный ответ. Правильная интерпретация формулы Кедрова состоит в том, что увеличение цилиндрического объёма, происходящее только за счёт увеличения площади поперечного сечения, при постоянной длине сопровождается уменьшением электрического сопротивления, и поэтому:

.

4.58. Решение. Рассмотрим объём крови с удельным сопротивлением - ρ в виде цилиндра высоты - l и площади поперечного сечения -S. Запишем формулу объёма цилиндра: V = S · l. Получим формулу для относительного изменения объёма цилиндра:

Получим формулу для относительного изменения электрического сопротивления цилиндрического проводника с удельным сопротивлением ρ, длиной lи площадью поперечного сечения –S:

;; считая ρ и постоянными и перейдя к конечным приращениям:.

Сравнив, полученные выражения, получим формулу Кедрова для реографии: . Применим формулу Кедрова к данным из условия задачи и получим окончательный ответ. Правильная интерпретация формулы Кедрова состоит в том, что уменьшение цилиндрического объёма, происходящее только за счёт уменьшения площади поперечного сечения, при постоянной длине сопровождается увеличением активной составляющей электрического сопротивления, и поэтому:

Ответ.

4.59. Решение. Выбор эквивалентной электрической схемы определяется ходом зависимости импеданса биологических тканей от частоты. Эта зависимость (дисперсия импеданса) такова, что наилучшей эквивалентной схемой для низких частот является схема параллельно соединённых резистора и конденсатора.

При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.

Рассматривая векторную диаграмму токов, получаем:

, ,

.

Ответ:

,

4.60. Решение. Выбор эквивалентной электрической схемы определяется ходом зависимости импеданса биологических тканей от частоты. Эта зависимость (дисперсия импеданса) такова, что наилучшей эквивалентной схемой для низких частот является схема параллельно соединённых резистора и конденсатора.

При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.

Рассматривая векторную диаграмму токов, получаем:

, ,

, , ,

.

Ответ.

.

4.61. Решение. При последовательно соединённых элементах сила тока через каждый элемент схемы одинакова. Напряжение, приложенное к схеме, складывается из напряжения на резисторе и напряжения на ёмкости. Напряжение и сила переменного квазистационарного электрического тока на ёмкости и резисторе не совпадают по фазе. Чтобы рассчитать абсолютную величину тангенса угла между током и напряжением для такой схемы используют векторную диаграмму напряжений.

, ,

.

Ответ: , .

4.62. Решение. Выбор эквивалентной электрической схемы определяется ходом зависимости импеданса биологических тканей от частоты. Эта зависимость (дисперсия импеданса) такова, что наилучшей эквивалентной схемой для высоких частот является схема последовательно соединённых резистора и конденсатора.

При последовательно соединённых элементах сила тока через каждый элемент схемы одинакова. Напряжение, приложенное к схеме, складывается из напряжения на резисторе и напряжения на ёмкости. Напряжение и сила переменного квазистационарного электрического тока на ёмкости и резисторе не совпадают по фазе. Чтобы рассчитать импеданс схемы используют векторную диаграмму напряжений.

, , .

=

Ответ: Z= . .

4.63. Решение. Характер дисперсии импеданса живых и отмирающих биологических тканей лежит в основе оценки их жизнеспособности. Коэффициент поляризации (коэффициент поляризации Тарусова) удобный критерий жизнеспособности. Коэффициент является отношением значения импеданса на низкой частоте к значению импеданса на высокой частоте . Коэффициент близкий по величине к единице характерен для отмирающей ткани. Это хорошо видно из зависимостей импеданса от частоты (дисперсий импеданса).

Эквивалентной схемой для низких частот является схема параллельно соединённых резистора и конденсатора.

При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.

Рассматривая векторную диаграмму токов, получаем:

, ,

, , ,

.

.

Эквивалентной схемой для высоких частот является схема последовательно соединённых резистора и конденсатора. При последовательно соединённых элементах сила тока через каждый элемент схемы одинакова. Напряжение, приложенное к схеме, складывается из напряжения на резисторе и напряжения на ёмкости. Напряжение и сила переменного квазистационарного электрического тока на ёмкости и резисторе не совпадают по фазе. Чтобы рассчитать импеданс схемы используют векторную диаграмму напряжений.

, , .

1,18

Ответ.1,18. Ткань не жизнеспособна.

4.64. Решение. Жизнеспособность ткани оценим по значению коэффициента поляризации Тарусова. Коэффициент является отношением значения импеданса на низкой частоте к значению импеданса на высокой частоте . Коэффициент близкий по величине к единице характерен для отмирающей ткани. Это хорошо видно из зависимостей импеданса от частоты (дисперсий импеданса).

Эквивалентной схемой для низких частот является схема параллельно соединённых резистора и конденсатора.

При параллельно соединённых элементах напряжение на каждом из элементов схемы одинаковое.

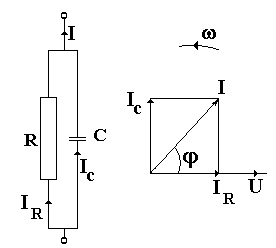
Рассматривая векторную диаграмму токов, получаем:

, ,

, , ,

.

.

Эквивалентной схемой для высоких частот является схема последовательно соединённых резистора и конденсатора. При последовательно соединённых элементах сила тока через каждый элемент схемы одинакова. Напряжение, приложенное к схеме, складывается из напряжения на резисторе и напряжения на ёмкости. Напряжение и сила переменного квазистационарного электрического тока на ёмкости и резисторе не совпадают по фазе. Чтобы рассчитать импеданс схемы используют векторную диаграмму напряжений.

, , .

Ответ.. Ткань жизнеспособна.