Математический анализ / Паша

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

(1 cos x )- 2-й порядок малости относительно

x при x 0 .

.pdf

Скачиваний:

Добавлен:

31.03.2015

Размер:

1.4 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

БИЛЕТ 16. Два определения предела

функции. Эквивалентность определений.

Пусть f (x) определена в некоторой выколотой окрестности т.
U (a, ) U (a, ) \ a x 0 x a

Определение 1 (Гейне):					lim	f (x) A , если		xn : xn	a ,
						x a
lim xn a , lim				f (xn ) A
	n			n
Замечание: xn
Замечание: xn				U (a, )
Определение 2 (Коши):					lim	f (x) A , если		0
						x a
( ) : x 0 x a .

	f (x) A	.

Замечание: , то есть U (a, ) U (a, ) .
Теорема: Определение 1 <=> Определение 2.
Имеем 0			( ) : x 0 x a .

	f (x) A	.
Возьмем произвольную					xn : xn a,		lim xn	= a =>
							n
N0 ( ) : n N0 ( )					xn a .
Обозначим N( ) N0					( ( )) . Тогда		n N( )
	0< an a .
Т.обр.
0		N( ) : n N( )
	f (xn ) A		., то есть lim			f (xn ) A
						n

БИЛЕТ 17. Теорема об арифметике пределов функций.

Теорема: Если существуют lim			f (x) и lim g(x) , то:
		x x		x x
		0			0
1).	lim f (x) g(x) lim f (x) lim g(x) .
	x x0	x x0		x x0
2).	lim kf (x) = k lim f (x) ( k - постоянная).
	x x	x x
	0	0
3).	lim	f (x)g(x) lim f (x)	* lim g(x) .
	x x0	x x0	x x0
4).	lim	f (x) g(x) lim f	(x)	lim g(x) ,
	x x0	x x0		x x0

если lim g(x) 0 .
	x x
		0
Доказательства:
Доопределив по непрерывности функции					f (x) и g(x)
в точке x0 , положив f (x0 ) = lim f (x) и					g(x0 )	= lim g(x)
		x x0				x x0
(это изменение функций не влияет на их пределы).
В точке x0 будут непрерывны функции f (x) g(x) ,
kf (x) ,		f (x)g(x) , f (x) g(x) (так как g(x0 )

= lim g(x) 0 . Поэтому в силу равенства

x x0

lim f (x) = f (x0 ) получим:

x x0

1).

2).

3).

lim f (x) g(x)
x x
0
lim kf (x) = kf (x0 )
x x
0
lim	f (x)g(x)	f
x x
0

f (x0 )

= k lim
		x x
		0
(x	0	)g(
	0

g(x0 ) = lim
	x x
		0
f (x)
x0 )	= lim	f
	x x
	0

(

(x) lim g(x) x x0

x) * lim g(x) x x0

. 4).

lim	f (x) g(x)
x x
0

(x	0	)
	0

g(x	0

)

	lim
	lim
		0
x x

f (x)

		lim

		0
	x x

g(x)

БИЛЕТ 19. Свойства пределов функций, связанные с неравенствами.

Теорема: Пусть lim	f (xn ) A
n
тогда A B .

Теорема: (Локальн. Огр.): Пусть

0 , M 0	: x 0 x
f ( x) M .

и lim x a

lim f x a

f (x	n

(x	n	)
	n

) B ,

A , тогда

( ) :

0 x a ( ) f ( x) A .

Возьмем 1. Тогда

A K f (x) A K

(1) : f (x)

0 x a

(1)

(1), M A

Теорема: Пусть lim f x 0

x 0 x a f (

1 (x x)

) A , lim g(x x a

g(x) . Тогда

) A

B и B

Возьмем произвольный

x	n	: x	n

lim x	n	a
n			ГЕЙНЕ

lim	f (x
n	n
n

	f (x		n	)
			n
				0
x				0
x		u
	0

) A, lim g(xn ) B , причем N0 : n N0

g(xn ) .
(a, )			(по теореме о предельном переходе в

неравенство) A B .

Теорема: Пусть lim f (x) A , lim g(x) B
x a	x a

: tx
	0	x a

f (x) h(x) g(x) . Тогда существует lim h
		x a
Возьмем произв. xn : xn	a , lim xn	a
	n

(x)

		lim	f (xn ) A , lim g(xn ) A , причем
ГЕЙНЕ		n				n
N	0	: n N		0	f (x	) h(x	) g(x	)
	0			0	n	n	n
						lim h(x) A
		0			сущ. x a				.
x0		u(a, )			сущ. x a				.

Теорема (об отделимости от нуля): Пусть lim f (xn ) A 0

x a

0 , M 0	: x
Доказательство:

0 x a

f (x) M

0 ( ) : x 0 x a ( )

f (x) A .

Возьмем

0 , тогда

(

) : x

x a

f (x) A

f (x)

A 2

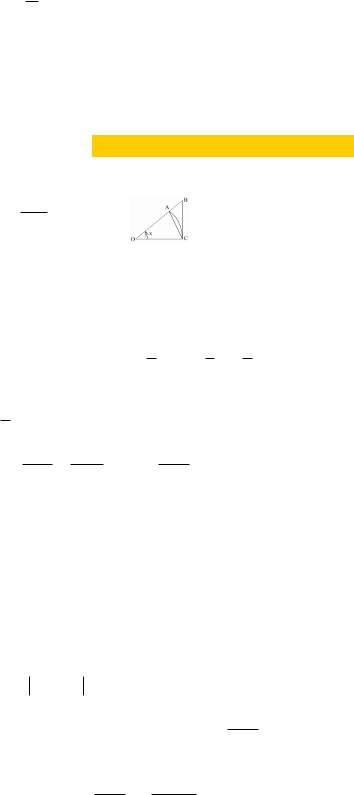
БИЛЕТ 21. Первый замечательный предел.

lim	sin x	1
	x
x 0
Для доказательства			возьмем вектор OAC

окружности радиуса 1 с центральным углом,

равным x (радиан), 0

BC OC . Тогда пл.

OAC < пл. OBC или

x			и проведем
	2

OAC		< пл. сект.

12 sin x 12 x 12 tgx .

Разделив все части этого неравенства на

1	sin x > 0, получим
2	sin x > 0, получим
2
1		x	1	или 1	sin x	cos x
1		sin x	cos x	или 1	x	cos x
		sin x	cos x		x
неравенство, доказанное для любых							x из

. Это

	интервала (0;
	интервала (0;	2
		2

	интервала (-
	интервала (-	2
		2

), верно для любого			x 0 из
;		) в силу четности функций,
	2

входящих в это неравенство.

Докажем, что lim cos x 1 x 0

( 0 1 cos x 2sin

) при x

А раз lim cos x 1 и

lim1 1, то lim

sin x

1 .

x 0

Кроме того: lim sin x

= lim

sin y

y x

x 0

x y

y 0

БИЛЕТ 22. Второй замечательный предел.

e lim (1 x)	1/ x	.
e lim (1 x)		.
x 0
На первый взгляд кажется, что (1 x)			1/ x	при
На первый взгляд кажется, что (1 x)				при
x 0 имеет пределом единицу (так как 1+ x

при x 0 имеет пределом единицу, а единица в любой степени есть единица). Но в степень

1/ x возводится 1+ x , а не единица. И вот из-за этой бесконечно малой добавки x предел не равен единице. Чтобы приблизительно представить себе

поведение функции	(1 x)	1	/ x	при малых	x

приведем таблицу значений этой функции:

x
(1 x)	1/ x
(1 x)

1/2	1/3	1/4	0.01	0.00
				1
2.25	2.37…	2.44…	2.7047…	2.71
				69
				…

Из этой таблицы видно, что с уменьшением x функция увеличивается. Оказывается, что это имеет место для всех x >0, а из этого следует, что функция имеет предел.

Доказательство:

Рассмотрим этот предел, как предел функции натурального аргумента на бесконечность. Тогда:

По определению Гейне:

lim

)

= e

Вычислим lim

(1 x)1/ x . Рассмотрим

(1 x)1/ x

) y .

lim

= y

= lim

x 0

По определению Гейне рассмотрим yk : lim yk .

nk N : nk yk nk 1 lim nk

	1	nk		1	yK
1			1
1			1
	nk 1
	nk 1			yk

	1	nK 1		1	nk		1
1			1			* 1
1			1			* 1

	nk			nk			nk

lim

(1 x)

1/ x

То есть

)

= e = x

= lim

x 0

(1 x)

1/ x

Также

lim

= y

lim

)

x 0

lim (

) y = lim

) y 1 (1

) e

y 1

БИЛЕТ 25. Сравнение бесконечно малых функций. Примеры.

Определение: (x) бесконечно малая функция при x x0 , если lim			(x) 0 .
		x x
		0
Определение: Пусть (x) и (x) - бесконечно малые функции при x x0 . Тогда:
1)	(x) и (x)	эквивалентны при x x0 ( (x) ~ (x) , x x0 ), если	lim		(x)		1.
1)	(x) и (x)	эквивалентны при x x0 ( (x) ~ (x) , x x0 ), если	lim		(x)		1.
			x x	0	(x)
			x x
2)	(x) , (x)	- бесконечно малые одного порядка малости при x x0	, если		lim		(x)
2)	(x) , (x)	- бесконечно малые одного порядка малости при x x0	, если		lim		(x)
					x x	0	(x)
					x x

малая более высокого порядка малость, чем

(x) .

(x)

- бесконечно

( (x) = 0	( (x) ), x x0 ), если lim			(x)	0 .
( (x) = 0	( (x) ), x x0 ), если lim			(x)	0 .
		x x	0	(x)
		x x
4). (x)	имеет	k -й порядок малости относительно (x) при x x0				, если lim		(x)		k 0 .
4). (x)	имеет	k -й порядок малости относительно (x) при x x0				, если lim		( (x))	k	k 0 .
						x x	0		k
							0

5). (x)	называется ограниченной относительно бесконечно малой функции (x) при x x0 , если
0 x x0		(x) C (x) .

Примеры:

1). lim x 0

2). lim x 0

3). lim

x 0

sin x	1	sin x ~ x
x

1 x 1		lim
x		lim
		x 0		x(			1
				x(			1
			sin			x
1 cos x	lim
1 cos x						2
x
x		x 0			x
				2
	1			0

при

x x

(sin

	x 0 .
			1
	1)		2

2x ) 0

(

1 x

cos x

x -бесконечные малости одного порядка).

x), cos x 1 0(x) )

С 0, 0 : x

5). x2 sin 1 x2

x2 sin x12

0 (x2 ),

x2 , c 1,

0 - произвольная.

БИЛЕТ 26. Эквивалентные бесконечно малые функции. Критерий эквивалентности.

Определение: функция (x) называется бесконечно малой при

Теорема (критерий эквивалентности):

x	0

, если

lim (x) x x0

=0.

Пусть (x) , (x)

(x) (x) - (

Доказательства:

-бесконечно малые функции при

x) . Тогда (x) ~ (x) при x

x x0 .

x	(x)
0

0( (x)), x

x	0

( ). Пусть (x) ~ (x) , x x0 , то есть

lim

(x)

x x

lim

(x)

(x) (x)

lim

(x)

1 =0,

(x)

x x0

то есть (x) 0( (x)), x x0 .

( ). (x)

0( (x)), x x0 ., lim

(x)

0 .

(x)

x x

lim

(x)

(x) (x) (x)

lim

(x)

=1.

(x)

x x0

Эквивалентные бесконечно малые функции. Теорема о замене на эквивалентные.

Определение: функция (x) называется бесконечно малой при	x x0	, если	lim (x)
			x x
			0
Теорема (о замене на эквивалентные):

=0.

Пусть функция (x) ~ (x) , (x) ~ (x) при x x0

и существует lim

x x0

(x)

. То есть выражение или функцию можно заменять на эквивалентное.

(x)

lim

(x)

= lim

(x)

= lim

(x)

x x

(x)(x)

, тогда существует и lim	(x)	= lim
x x0	(x)	x x0

1 1

БИЛЕТ 27. Сравнение бесконечно малых функций. Примеры.

Определение: (x) бесконечно малая функция при x x0 , если lim			(x) 0 .
		x x
		0
Определение: Пусть (x) и (x) - бесконечно малые функции при x x0 . Тогда:
1)	(x) и (x)	эквивалентны при x x0 ( (x) ~ (x) , x x0 ), если	lim		(x)		1.
1)	(x) и (x)	эквивалентны при x x0 ( (x) ~ (x) , x x0 ), если	lim		(x)		1.
			x x	0	(x)
			x x
2)	(x) , (x)	- бесконечно малые одного порядка малости при x x0	, если		lim		(x)
2)	(x) , (x)	- бесконечно малые одного порядка малости при x x0	, если		lim		(x)
					x x	0	(x)
					x x

малая более высокого порядка малость, чем

(x) .

(x)

- бесконечно

( (x) = 0	( (x) ), x x0 ), если lim		(x)	0 .
( (x) = 0	( (x) ), x x0 ), если lim		(x)	0 .
		x x0	(x)
4). (x)	имеет k -й порядок малости относительно (x) при x x0 , если lim					(x)		k 0 .
4). (x)						( (x))	k	k 0 .
				x x	0	( (x))
				x x
5). (x)	называется ограниченной относительно бесконечно малой функции (x) при x x0 , если
0 x x0		(x) C (x) .

Примеры:

1). lim	sin x	1 sin x ~ x
	x
x 0

2). lim	1 x 1		lim
2). lim	x		lim
x 0			x 0		x(			1
					x(			1
				sin			x
	1 cos x	lim
3). lim	1 cos x						2
3). lim	x
x 0	x		x 0			x
					2
		1			0

при

x x

(sin

	x 0 .
			1
	1)		2

2x ) 0

(

(1 cos

1, x -бесконечные малости одного порядка).

0(x), cos x 1 0(x) )

4). (x) …
lim	1 cos x				1	(1 cos x )- 2-й порядок малости относительно x при x 0 .
lim						(1 cos x )- 2-й порядок малости относительно x при x 0 .
x 0		x2		2
5). x2 sin			1	0 (x2 ), x 0
5). x2 sin			x2	0 (x2 ), x 0
			x2
x2 sin		1	x2 , c 1, 0 - произвольная.
x2 sin		x2	x2 , c 1, 0 - произвольная.
		x2

С 0, 0 : x

БИЛЕТ 28. Определения непрерывности функции в точке. Простейшие свойства непрерывных функций.

Определение 1: Функция		f (x) непрерывна в точке		x0	, если	lim f (x) f (x0 ) .
						x x
						0
Определение 2: Функция		f (x) непрерывна в точке		x0	, если	xn :		lim xn x0 ,		lim f (xn )	f (x0
								n		n
Определение 3: Функция		f (x) непрерывна в точке		x0	, если	0		( ) : x		x x0
f (x) f (x0 ) .
Свойства непрерывных функций:
Теорема 1 (локальная огр.): Пусть функция f (x) непрерывна в точке								x0	, тогда 0, M 0 :		x
f (x) M .
Теорема 2 (отделимость от 0): Пусть функция f (x) непрерывна в точке									x0 и f (x0 ) 0 , тогда
0, M 0 : x x x0			f (x) M . ( A		f (x0 )) .
Теорема 3 (арифметика непрерывных функций): Пусть f (x) , g(x)							непрерывны в точке x0 , тогда:
1).	f (x) g(x) непрерывна в точке x0 .
2).	f (x) g(x) непрерывно в точке		x0 .

) .

x x	0
	0

3). Если g(x) 0 , то	f (x)	непрерывно в точке x0 .

	g(x)
	g(x)
БИЛЕТ 29. Непрерывность сложной функции.
Теорема: если функция t g(x) непрерывна в точке x0 , а функция				y f (t) непрерывна в точке t0 g(x0 ),	то сложная
функция f (g(x)) непрерывна в точке x0 .
Доказательство:
Возьмем число >0. Так как функция f (t) непрерывна в точке t0			g(x0 ), то можно подобрать такое число 1		0 , что
f (t) f (t0 ) для любого t , такого, что t t0 . (1)

А так как функция t	g(x) непрерывна в точке x0 , то для положительного числа 1 можно подобрать такое число
что
g(x) g(x0 ) 1	для любого x	, такого, что		x x0 . (2)
Возьмем любое число x такое, что		x x0		. Тогда в силу (2) число t g(x) удовлетворяет неравенству
g(x) g(x0 ) 1	, и поэтому в силу (1)		f (g(x)) f (g(x0 )) . Так как все эти вычисления проведены для любого
>0, то непрерывность функции f (g(x)) в точке				x0 доказана

0 ,

БИЛЕТ 30. Классификация разрывов. Примеры.

Определение:	x0 -точка разрыва функции f (x) , если в точке x0
Определение:	точка x0 -точка устранимого разрыва функции f (x

функция f (x) не является непрерывной.

) , если существует lim f (x) , но f (x) неопределена в

точке	x0	, либо	lim	f (x)	f (x0 ) .
			x x
			0

Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:

~		f (x), x

f			f (x), x
	lim
	x x0

x	0

x		0

   

- непрерывна в точке

x	0

Пример:

f (x)

x x

lim f (x) 1,			x 0 - точка устранимого разрыва f (x) .
x 0
Если	lim	f (x)	не существует, то x0 -точка неустранимого
	x x
	0
разрыва		f (x) .

Определение: Пусть точка x0

-точка неустранимого разрыва функции f (x) , тогда:

1)	если существует					lim	f (x) A , то lim		f (x) B .
						x x0 0	x x0	0
2)	если		A B	, то		x0 -точка разрыва функции			f (x) 1-го рода.
3)	если		A B	, то x0 -точка разрыва функции					f (x) 2-го рода.
Примеры:
1). f (x) sgn x				1, x 0
1). f (x) sgn x							.
				1, x 0
lim f (x) 1, lim				f (x) 1
x 0			x 0
x 0 - точка разрыва					f (x) 1-го рода.
2). f (x)		1	.
2). f (x)			.
		x
lim f (x) , lim					f (x)
x 0			x 0

x 0	- точка разрыва
	1

f (x)

2-го рода.

3).

f (x) 2	x

lim f x 0

x 0 4). f (

(x) ,		lim
		x 0
- точка разрыва
x) sin	1
	x

f (x) f (x)

2-го рода.

x	n

y	n



1	0	f (x		) sin(2 n) 0 0
			n
2 n				n
	n

	1	0	f ( y		) sin(		2 n) 1	1
		0	f ( y	n	) sin(	2	2 n) 1	1
		n		n				n
	2 n

2
2

lim sin 1

x 0 x

lim	f (x)
x 0

не существует

, lim	f
x 0

(x)

точка

x 0 - точка разрыва f (x) 2-го рода.

. Точка x 0 - точка разрыва f (x) 2-го рода

БИЛЕТ

Пусть

f (x)

32.

Первая теорема Вейерштрасса.

a,b . Тогда

f (x) ограничена на a,b .

Доказательство:
Докажем, что M : x [a,b]		( f (x)) M .
Предположим противное, то есть M 0 x [a,b] :					f (x) * M . Возьмем M		=1,2,3…
Получим xn :
1) xn [a,b] n
2)	f (xn ) n
Из этих определений получаем		lim f (xn ) .
		n
xn	[a,b]=> xnk -подпоследовательность последовательности xn :
lim xnk x * .
n
xnk [a,b] x* [a,b] f (x) -непрерывна в точке					x * =>	lim f (xnk ) f (x*) .
						n
xnk -подпоследовательность последовательности			xn : lim f (xn ) => lim f (xnk ) . Противоречие.
					n	n
Замечание: Замкнутость [a,b] по существу. f (x)			1	, x (0,1]		, f (x) C(0,1] , но	f (x)
Замечание: Замкнутость [a,b] по существу. f (x)				, x (0,1]		, f (x) C(0,1] , но	f (x)
			x

Не является ограниченной на

(0,1] .

БИЛЕТ 33. Вторая теорема Вейерштрасса.

Пусть f (x) C a,b . Тогда x1 , x2	[a,b] : f (x1 ) sup f (x), f (x2 ) inf f (x),
	[a,b]	[a,b]
	[a,b]

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в папке Математический анализ

#
31.03.20153.96 Mб81Ответы.doc
#
31.03.20151.8 Mб41Ответы.pdf
#
31.03.20151.4 Mб21Паша.pdf