56. Локальный экстремум функции. Необходимое условие локального экстремума.

57. Первое достаточное условие локального экстремума.

58. Второе достаточное условие локального экстремума.

Теорема 1. Необходимое условие экстремума.

Пусть точка х0 является точка экстремума для функции f(x). Тогда, если существует f’(x0), то f’(x0)=0, либо f’(x0) не существует.

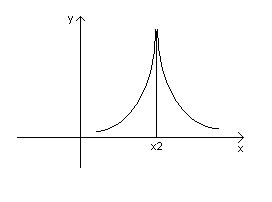
В точке х1 – min; в точке х2 – max.

Теорема 2. Достаточное условие строгого extr в терминах первой производной.

Пусть f(x) дифференцируема в некой окрестности точки х0, и в точке х0 f(x) непрерывна. Если f’(x) при переходе через точку х0 меняет знак, то точка х0 является точкой строгого экстремума, при этом 1)если при , а при

то в точке х0 – минимум. 2)если при , а прито в точке х0 максимум.

Доказательство.

Докажем 1) .Теорема Лагранжа. а) Если х-х0>0 и. б) если х-х0<0 и, т.е при переходе через точку х0не меняет свой знак:>0, т.е точка х0-точка минимума.

2)Доказательство аналогично.

Достаточное условие строгого экстремума в терминах старшей производной.

Пусть в точке х0 у функции f(x) существует n производных, причём Тогда, еслиn=2k, то в точке х0 экстремум, и если Еслиn=2k+1 в точке х0 нет экстремума и точка х0 точка возрастания. Если и точка убывания,если.

Следствие. Если в точке х0 у функции f(x) существует, то, если>0, то в точке х0 минимум,<0,то в точке х0 максимум (k=1).

Доказательство.

Разложим функцию f(x) в ряд Тейлора.

или знакопределяется первым слагаемым, еслиn – четное, то знак зависит от знака. По этому, еслито>0 – минимум.то<0 – максимум. Еслиn – нечетное, то знак зависит оти, т.е. при переходе через точку х0 знакменяется, следовательно в точке х0 экстремума нет.

Следствие.

. f’’(x0)>0, >0 – минимум;f’’(x0)<0, <0 – максимум.

59. Выпуклость функции. Достаточное условие выпуклости функции.

Выпуклости функции. Точка перегиба.

Опр. Функция f(x) на интервале (a,b) называется выпуклой вверх (выпуклой вниз), если

()

Геометрически это означает что кривая y=f(x) лежит выше(ниже) прямой.

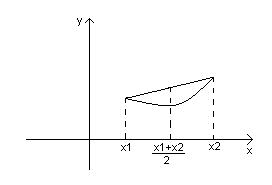
Достаточное условие строго выпуклости.

Теорема. Если на интервале (a,b) f’’(x)>0, то f(x) выпукло вниз, если f’’(x)<0, то f(x) выпукло вверх.

Доказательство

Рассмотрим разность х2-х1>0

а)Если выпукла вниз.

б) Если выпукла вверх.

60. Связь выпуклости функции и касательной к графику функции

(формулировка).

64. Точка перегиба функции. Необходимое условие для точки перегиба.

Опр. Точка х0 для функции f(x) называется точкой перегиба, если она является концом интервала выпуклота вверх(вниз) и началом интервала выпуклота вниз(вверх)

Необходимое условие точек перегиба.

Если функция дважды непрерывна, дифференцируема в точке х0 и если точка х0 является точкой перегиба, то f’’(x0) = 0

Доказательство. Если бы f’’(x0)>0 то в некоторой окрестности точке х0 f(x) была выпукла вниз. Если бы f’’(x0)<0 то в некоторой окрестности точке х0 f(x) была выпукла вверх. Но это противоречит определению точке перегиба: точка перегиба не принадлежит ни какому интервалу выпуклости.

65. Достаточные условия для точки перегиба (2 теоремы).

Достаточное условие точки перегиба.

Если функция f(x) дважды дифференцируема в некоторой окрестности точке х0 кроме, быть может, самой точки х0, но f(x) непрерывна в точке х0 и ее производная меняет знак при переходе через точку х0, то в точке х0 – точка перегиба.

Доказательство.

Т.е. в случае (1) точка х0 является концом интервала выпуклости вверх и началом интервала выпуклости вниз, следовательно точка х0 точка перегиба. В случае (2) точка х0 является концом интервала выпуклости вниз и началом интервала выпуклости вверх, следовательно х0 точка перегиба.

Замечание. Заметим, что если функция y=f(x) выпукла вниз, то ее график лежит выше касательной, если функция y=f(x) выпукла вверх, то ее график лежит ниже касательной.

Теорема. Пусть функция f(x) обладает следующим условием непрерывна в точкеx0 и .n-четное y= f(x) выпукла вверх, если и выпукла вниз, если,n+1-нечетное- точка x0-точка перегиба.

Доказательство.

66. Асимптоты графика функции.