50. Теорема Коши для дифференцируемых функций.

Теорема Коши (обобщенная формула конечных приращений).

Теорема Коши.

Пусть функции иg(x) определены на интервале (a,b)

1) иg(x) непрерывны на [a,b];

2) иg(x) дифференцируемы на (a,b) причем , тогда

Доказательство.

Рассмотрим функцию параметрвыбрали из условия

.

Для функции F(x) выполнены условия теоремы Ролля. Формулировка теоремы Ролля Сравнивания формулы для, получим утверждение теоремы.

Следствие.

Теорема Лагранжа. Если ,то.

51. Правило Лопиталя.

Правило Лопиталя.

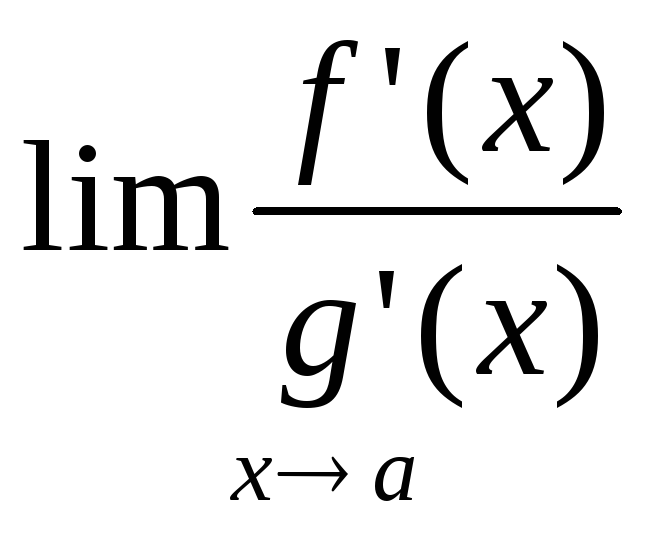Для раскрытия неопределенности вида .Пустьиg(x) определены в окрестности точки а, кроме, быть может, самой точки а и . И пусть в окрестности точки а существуют. Если существует, то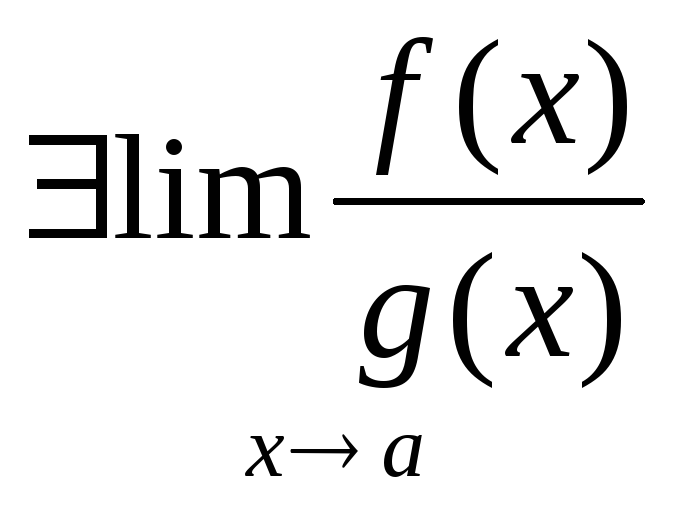и эти пределы равны.

Доказательство.

1. а - конечное число. Доопределим функции иg(x) в точке х=а, по непрерывности: f(a)=g(a)=0. Рассмотрим отношение . Здесь(использовали теорему Коши). Перейдем к пределу при(т.ки если, то).

2. надо сделать замену, x=1/t, тогда ,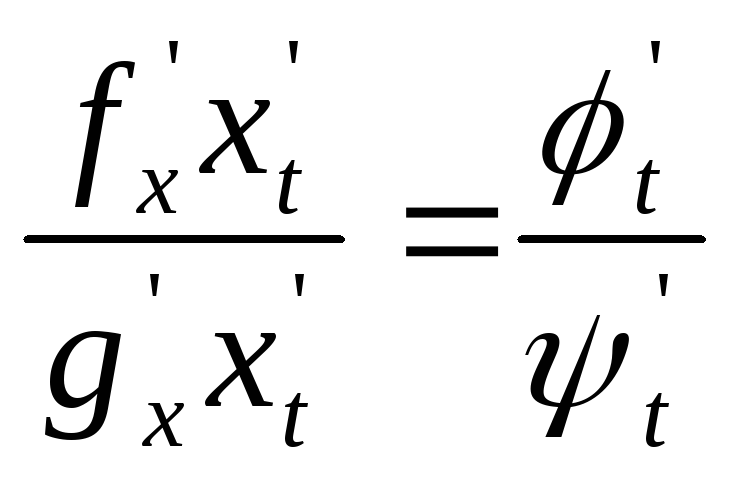и правило применяется к новой функции.

Теорема 2.

Пусть иg(x) определены и дифференцируемы в окрестности точки а и .Если, тои они равны.

Замечание.

В формулировке теорем необходимо потребовать, чтобы .

-теорема 1 доказана. -теорема 2 формулировка.

.

Пример, когда нельзя применять правило Лопиталя .

Вычислим предел отношения производных он не существует, т.к. не существует предел числителя и знаменателя. Правило Лопиталя применять нельзя.

Вычислить.

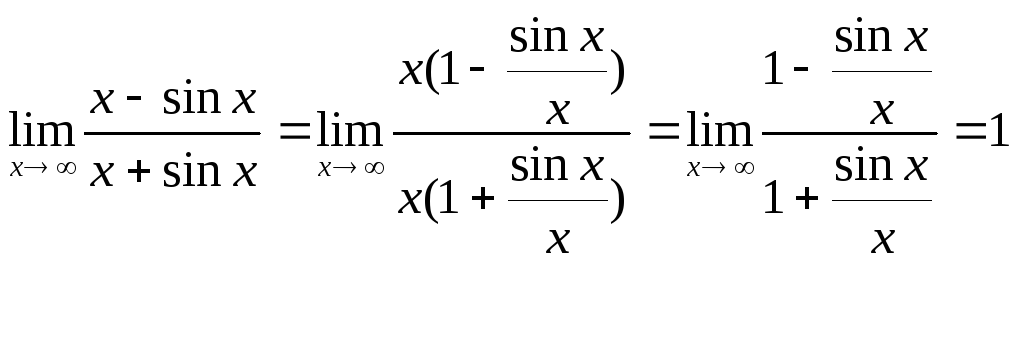
52.53.54 Формула Тейлора с остаточным членом в форме Пеано. Формула Тейлора с остаточным членом в форме Лагранжа. Формулы Тейлора для элементарных функций.

Формула Тейлора.

Пусть функция дифференцируема в точке, тогда, где-бесконечно малая более высокого порядка чем., гделинейная функция, причем.

Можно расписать, что , т.е в окрестности точкифункцияf(x) ведет себя как линейная. Поставим более общую задачу: для функции y=f(x) найти многочлен порядка n, который обладает следующими свойствами:

Многочлен будем писать в виде

первые равенства получаются путем дифференцирования формулы для и подстановки. Вторые равенства - это требуемые свойства.f(x) у которого существует производная до n порядка включительно можно найти коэффициенты

Многочлен ,,многочлен Тейлора для функцииf(x).

Обозначим

Рассмотрим функцию и вычислим

Т.о получим ,остаточный член формулы Тейлора.

Пусть функцияf(x) определена на интервале (a,b) и в каждой точке x0 принадлежащей интервалу (a,b) имеем производную до n порядка включительно, тогда , где

Единственность многочлена Тейлора.

Пусть функция представлена в окрестности точкимногочлена вида

Доказательство.

Если гдееё многочлен Тейлора и есть у нас другой многочленнадо показать, что коэффициенты одинаковы

Пусть сократим на

. пусть сократим наи т.д.многочлен Тейлора единственен.

55. Признак монотонности функции.

На рисунке нарисован график функции, всюду имеющей производную. В точкекасательная ки осьобразуют острый угол, поэтому ее угловой коэффициент, равный, положителен. Но. Следовательно,. И так будет в любой точке интервала, где функциямонотонно возрастает. Напрашивается вывод: если на интервале, то на этом интервале функция монотонно возрастает. Далее, в точкекасательная кобразует с осьютупой угол, поэтому ее угловой коэффициент, равныйотрицателен. А так как, то. Вывод: если на интервале, то на этом интервале функция монотонно убывает. В точкефункция имеет максимум. На чертеже ясно, что в этой точке касательная кпараллельна оси, и поэтому ее угловой коэффициент равен нулю, так что. При этом слева от этой точки, а справа.

Теорема (достаточный признак монотонности).

1). Если на отрезке, томонотонно возрастает на.

2). Если на отрезке, томонотонно убывает на.

Доказательство:

Возьмем любые числа и, причем<, из интервала. По формуле Лагранжа получаем:,, и поэтомупринадлежит интервалу. Так как, то в первом случае, то есть, а во втором, то есть, что и требовалось доказать.