18

Лабораторная работа № 2 определение длины волны света методом колец Ньютона

Цель работы: изучение явления интерференции на примере колец Ньютона.

1. Введение

Явление интерференции наблюдается при наложении когерентных волн (см. введение к работе 1). Любые два "естественных" источника света (солнце, свеча, лампа накаливания) не являются когерентными. Для наблюдения интерференции пользуются методом разделения световой волны от одного источника на две волны, идущие разными путями в одну точку. В области наложения волн возникает интерференционная картина. Разделение волн осуществляется различными способами. Одним из них является метод колец Ньютона.

Кольца Ньютона представляют собой так называемые линии равной толщины – частный случай интерференции в тонких пленках.

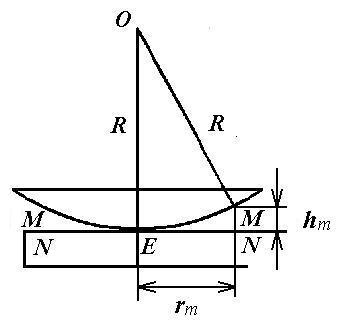
Когерентные волны получаются делением одной волны на две, образующиеся при отражении падающего света от верхней и нижней границ воздушной прослойки. Воздушная прослойка MEN располагается между поверхностью плоской пластинки и соприкасающейся с ней в точке E сферической поверхностью линзы (рис. 1).

Рис. 1	Рис. 2

Кольца Ньютона можно наблюдать как в отраженном, так и в проходящем свете. В данной работе наблюдение ведется в отраженном свете.

Рассмотрим тонкую воздушную прослойку клиновидной формы между поверхностями ME и NE (см. рис. 2). На нее падает почти по нормали плоская монохроматическая световая волна. На рис.2 угол падения этой волны  для наглядности увеличен (реально   0).

Падающая волна, направление распространения которой характеризуется лучом 1, частично отражается от поверхности ME (луч 2), а частично, преломляясь, проходит через воздушный зазор (луч AB). Отразившись от поверхности NE (луч BC) и вновь преломившись на поверхности линзы ME, эта волна формирует когерентный световой пучок (луч 3). Полученные таким образом две когерентные световые волны (лучи 2 и 3), заполняющие всё пространство выше воздушного клина, перекрываются и, накладываясь друг на друга, дают интерференционный эффект вблизи и выше выпуклой поверхности линзы MEM. Амплитуды этих волн мало отличаются друг от друга, что важно для получения контрастной интерференционной картины. Локализованные вблизи выпуклой поверхности линзы интерференционные полосы, в виде колец, можно наблюдать непосредственно глазом, фокусируя его на поверхность MEM. Микроскоп позволяет увеличить наблюдаемую картину.

Оптическую разность хода волн 2 и 3 можно найти по разности хода их лучей (луч – это перпендикуляр к волновой поверхности). Из рисунка 2 получим

,

здесь n – показатель преломления стекла линзы.

Так как и и, кроме того, , то в результате подстановки получим

, (1)

здесь h = BK – толщина клина в данной области.

Слагаемое /2 появляется в формуле (1) из-за того, что условия отражения волн 2 и 3 на границе раздела двух сред различны. Волна 3 сформирована путем отражения от пластинки (от среды оптически более плотной, чем воздух), в результате чего фаза отраженной волны меняется на  или, как говорят, происходит "потеря" полуволны ( /2). Волна 2 формируется при отражении от воздушной среды (оптически менее плотной, чем стекло) без потери полуволны.

В нашем случае одной из границ воздушной прослойки является сферическая поверхность линзы, поэтому интерференционная картина будет представлять собой систему чередующихся темных и светлых колец – колец Ньютона. В условиях эксперимента свет падает нормально к плоской поверхности линзы (рис. 1).

Тогда формула (1) с учетом того, что   0 и   0, примет вид

. (2)

С другой стороны, если

,m = 0, 1, 2, 3, ...,. (3)

то будет наблюдаться интерференционный максимум (m – порядок интерференции), при

(4)

будет наблюдаться минимум интенсивности света.

Из (2) и (3) получаем условие интерференционного максимума

или. (5)

Условие интерференционного минимума

. (6)

Очевидно, что m одновременно является номером светлого или темного кольца.

Толщина прослойки может быть определена по известному радиусу кривизны линзы R и радиусу кольца r_m (см. рис. 1)

(здесь мы пренебрегаем , учитывая, чтоR >> h_m). Тогда

. (7)

Учитывая (6), получим для темного кольца

или. (8)

Так как обеспечить идеальный контакт линзы и пластинки в точке E (рис. 1) невозможно из-за попадания пылинок, то номер кольца, вообще говоря, не соответствует порядку интерференции m. Дело в том, что если линзу немного приподнять над пластинкой, то кольца стянуться к центру, так как данное значение h будет реализовано ближе к центру. Поэтому в формуле для расчета длины волны следует использовать комбинацию из двух значений радиусов интерференционных колец r_k и r_m, в которую входит разность (m – k), что позволяет исключить влияние зазора на результат расчета.

, где (m  k)

или, выражая радиусы колец через их диаметры, получим

, (9)

где d_m и d_k– диаметр соответствующего темного кольца.

Если падающий свет немонохроматичен и имеет спектральный интервал от  до +_ф, то количество видимых интерференционных колец будет ограничено величиной m = /_ф (см. лаб. раб. № 1, формулу 4). Соответственно толщина слоя для области интерференции будет иметь предельное значение

.

Найденное значение m позволяет также оценить длину когерентности

.