Лекция № 4

Простое и сложное нагружение.

Теорема А.А.Ильюшина о

Простом нагружении.

1 Простым называется такое нагружение, при котором компоненты девиатора

напряжений возрастают пропорционально некоторому параметру.

В противном случае нагружение сложное :

S_jk=S_jk⁰

2 Иногда (по Качанову) простым называется , когда _jk=_jk⁰

при этом формулировка 1 выполняется.

Теорем а.А. Ильюшина. Для того , чтобы нагружение было простым , достаточно , чтобы:

1. Все внешние нагрузки изменялись пропорционально одному параметру:

X_j=X_j⁰ ;P_j=P_j⁰

2.Между напряжениями и деформациями существовала степенная

зависимость :T=A^m ,m1

_j =A^m_j m=0-условие пластичности Губера-Мизеса.

3.Материал был несжимаем =0.

Пример: тонкостенная труба

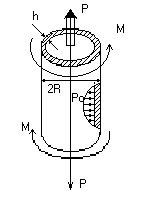₁₁=P/2Rh ₂₂=P₀R/h ₁₂=M/2R²h

Если P=P₀ ; P₀=P₀⁰ ; M=M⁰ то нагружение простое.

O₁ – простое нагружение ; О₂ – сложное нагружение.

Сначала скручиваем , потом растягиваем, затем загружаем давлением P₀ ,

Получаем сложное (ступенчатое) нагружение(0О₃).

При простом нагружении форма тензора напряжений и его главные оси все время сохраняются.

При сложном нагружении направление главных осей и взаимоотношение главных напряжений могут изменятся.

Вывод соотношений деформационной

теории из уравнений Прандтля-Рейсса

при простом нагружении для тела

с изотропным упрочнением.

Теории течения (основанные на постулате Дракера) и деформационная теория в случае простого нагружения приводят к одинаковым уравнениям:

d_jk=æ_jklmd_lm+d(T)(_jk-_jk) использованы соотношения Леви-Мизеса.

æ_jklmd_lm=d_jk^(e) d(T)(_jk-_jk)=d_jk^(p)

Пусть материал изотропен , девиаторы  и  подобны:

(_jk-_jk)=2(_jk^(e)-1/3_jk)

=G – модуль сдвига.

Тогда:

(_jk^(e)-1/3_jk)=(1/2)* (_jk-_jk)  _jk^(e)= (1/2)* (_jk-_jk)+ 1/3_jk (1)

Для пластической деформации.

Т.к. нагружение простое, то S_jk=S_jk⁰

T=1/2(_jk-_jk) (_jk-_jk)=T₀ =T/T₀

Таким образом ,для каждого пути нагружения параметр (Т) зависит от величины  (изменяется только ).

Т=Т⁰

d_jk^p=d(T) (_jk-_jk); d_jk^p= d(T⁰) (_jk⁰-⁰_jk);

d_jk^p= (T⁰)T⁰d (_jk⁰-⁰_jk);

d_jk^p= F()d (_jk⁰-⁰_jk); F()=(T⁰)T₀;

d_jk^p= F()(_jk⁰-⁰_jk)=(T)(_jk-_jk) ;

(T)=F()/ ; _jk^p=l_jk^p ; l_jk=l_jk^e +l_jk^p;

l_jk=S_jk ; l_jk=(T)S_jk+1/2G*S_jk;

l_jk=S_jk

=(T)+1/2G

Мы получили соотношения деформационной теории из соотношений теории течения. Значит, в случае простого нагружения обе теории течения для тела с изотропным упрочнением и деформационная теория дают одинаковые результаты.

Аналогичные результаты можно получить для тела с анизотропным упрочнением.

Достоинства и недостатки

деформационной теории.

Достоинства :простота пользования теории. Напряжения и деформации связанны однозначно, нет необходимости решать уравнение Прандтля-Рейсса. Достаточно знать лишь конечное напряженное состояние.

Недостатки : Результаты не зависят от пути нагружения по этому в случае

простого нагружения эту теорию можно применять , а в случае сложного нагружения она приводит к неверным результатам.

Постановка задач в теории

идеального упругопластического

тела.

НаSp:P_j=_jkn_k; P_j=_jkn_k

На Su: заданыu_j=u_{j0 ,} u_j=u_j0

В V:_jk/x_k+X_j=0 - статически возможное поле напряжений.

Существенное влияние оказывает способ приложения нагрузки, а также предыстория нагружения(см. занятие №3).

При нагружении , если _тТ , тело целиком находится в упругой области.

При дальнейшем увеличении нагрузки (Т=_т) в теле образуются пластические области.

Понятие о границах раздела.

Вообще говоря ,в теле , при нагружении возможны три области:

V_l– деформации все время упругие(упругая область)

V_p– в данный момент появляется пластическая деформация

V₀– ранее были пластические деформации , но в данный момент закон деформирования упругий (есть остаточные пластические деформации).

Границами (поверхностями) раздела называют поверхности , которые разделяют V_p иV_l,V_p иV₀.

Следует отличать упругие области в теле и упругую область в пространстве напряжений (внутри S_p) .

Обычно рассматривают V_pиV_l

“+” кV_p

“-” кV_l

Условия на границах

слабого разрыва.

Здесь переход от V_lкV_pидет безтрещин и сдвигов

1) u_j⁺=u_j^- - нет трещин и проскальзывания

2) _jk⁺=_jk^-- т.е. условие непрерывности деформаций..

Т.к. для упругой области d=0 , то на границе:

3) d=0d_jk⁺=æ_jklmd_lm⁺d_jk^-=æ_jklmd_lm^-

т.е. на границе деформации упругие.

4) _кз⁺=_кз^-- условие равновесия.

5) Для изотропного материала:

₁₁⁺=1/E[₁₁⁺-(₂₂⁺+₃₃⁺)]=₁₁^-=1/E[₁₁^--(₂₂^-+₃₃^-)] 

 (2)

₂₂⁺=1/E[₂₂⁺-(₁₁⁺+₃₃⁺)]=₂₂^-=1/E[₂₂^--(₁₁^-+₃₃^-)] 

Из условия непрерывности ₃₃следует непрерывность₁₁,₂₂

Т.е. _jk⁺=_jk^-(3)

Итак на границе слабого разрыва должны выполнятся соотношения:

uj+=uj- (jk+=jk-) jk+=jk- d=0

(4)

Эти условия не зависят от того, используется ли теория течения или деформационная теория. Для некоторых пластических тел оказывается возможным и реализуемым разрывные решения. Общая теория таких решений берет начало с работ С.А.. Христиановича / 1936 г./ и получила существенное развитие в работах В. Прагера /1956 г./

Условие на границах сильного разрыва.

Здесь переход отVp к Vl без трещин , но со сдвигами :

т.е. U₃⁺=U₃^- - нет трещин.

Взаимное смещение допускается , т.е.

U_1,2⁺U_1,2^- - хотя бы одно из перемещений разрывно.

_k3⁺=_k3^- - условия равновесия.

Пример:

П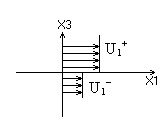оверхность разрыва тангенциальных смещений.

Пусть U₁ на границе меняется скачком.

Можно рассмотреть это как предельный переход.

Применим ассоциированный закон течения (соотношение Леви-Мизеса):

d_jk^(p)=d (_jk-_jk); d0.

Здесь толькоd₁₃^(p)0 , остальные d_jk^(p)=0 - на границе

₁₃0 ,остальные _jk=0

Условие текучести Мизеса: T² - _T²=0 

1/2(_jk-_jk) (_jk-_jk)= _T²,тогда ,очевидно , что т.к. только ₁₃0 , то получим, что на поверхности разрыва:

₁₃=_T ! d₁₃^(p)= d_T (5)

Таким образом ,поверхности сильного разрыва направлены по площадкам, где действуют максимальные касательные напряжения и называются поверхностями скольжения .