Лекция № 5.

Теория предельного равновесия идеальной упруго-пластической среды.

На тело или конструкцию, закреплённую определённым образом, действуют статические нагрузки. Требуется определить максимальную эффективность нагрузок, соответствующих пластическому деформированию конструкции. Такие значения нагрузок приводят к превращению конструкции в пластический механизм, причём деформации конструкции могут возрастать неограниченно при постоянном достигнутом значении нагрузок. Соответствующие значения нагрузок называются предельными, их величина определяет несущую способность конструкции.

Для принятой идеально-пластической схемы деформирования материала уровень напряжений является при этом максимальным, т.е. предельным. В связи с чем называется задача о предельном равновесии.

Пусть все внешние усилия возрастают пропорционально одному параметру. Введём обозначения.

Статически возможное состояние называется безопасным, если во всех точках тела напряжения лежат строго внутри поверхности текучести (т.е.) .

С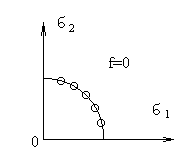татически возможное состояние называется допустимым, если для всех точек тела выполняется условие .

Коэффициентом запаса, соответствующим некоторой системе нагрузок , не превышающих предельные, назовём некоторое число n1, если нагрузки образуют систему предельных нагрузок.

Если системе внешних сил соответствует некоторое статически безопасное поле напряжений , то можно найти такое число , что напряжения станут статически допустимыми. Число назовём статически допустимым множителем.

Распределение скоростей перемещений назовём кинетически допустимым, если оно удовлетворяет условию несжимаемости и граничным условиям . Распределение скоростей деформации , соответствующие кинематическому допустимому полю скоростей перемещений, назовём кинематически допустимым.

Первая теорема теории предельного равновесия.

Нагрузка, прикладываемая к телу в любой последовательности, будет меньше предельной, если в любом случае существует статически безопасное распределение напряжений.

Другая формулировка :

Коэффициент запаса является наибольшим допустимым множителем . Статически допустимый множитель является нижней оценкой коэффициента запаса.

Покажем эквивалентность обеих формулировок :

Если в теле при данных нагрузках существует безопасное поле напряжений , то поле напряжений /- малое число / будет также статически безопасным и следует согласно формулировке. А нагрузки будут меньше предельных , откуда .

Доказательство первой теоремы.

Поставим некоторые ограничения (упрощения) :

Рассмотрим вначале вспомогательную задачу. Докажем что при пластическом течении , для действительных напряжений и деформаций. Применим минимальный принцип для скоростей напряжений :

второй член = 0, т.к. .

- любое статически возможное состояние, т.е. может быть .

Согласно минимальному принципу , где - функционал действительных состояний.

г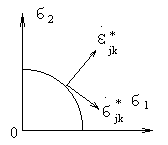де первый член суммы – положительно определённая квадратичная форма, а второй =0 т.к. тело идеальное упруго-пластическое

Т.к. тело идеальное упруго пластическое, т.е. пластические деформации достигаются при .

при этих условиях задача имеет тривиальное решение .

Значит , но т.к. для действительного состояния .

Т.е. в предельном состоянии упругие составляющие деформаций приращений не получат.

Перейдём к доказательству.

Действуют нагрузки и . Пластическое ткчение появляется при определённых нагрузках и . Предположим, что при исходных нагрузках в теле в теле существует безопасное поле напряжений . Используем уравнения скоростей виртуальных работ применительно к компонентам , , где - действительные распределения напряжений и скоростей деформации, соответствующих предельным нагрузкам.

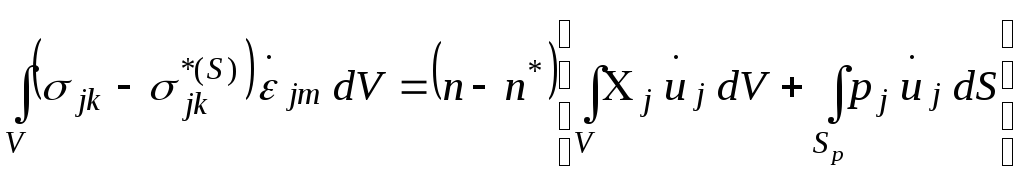
Учтём, что .

Интеграл в правой части неотрицателен/следствие из постулата Драккера/

Выражение в квадратных скобках представляет скорость работы внешних сил и всегда положительно.

Поэтому, окончательно , что доказывает теорему.

Если в теле определено некоторое кинематически допустимое поле скоростей деформаций , то ему соответствует диссипация механической энергии .

Системе внешних усилий , не превышающих предельные и скоростям перемещений будет соответствовать некоторая скорость изменения работы / мощность / внешних сил . Можно найти такое число , которое обеспечит равенство . Число назовём кинематически допустимым множителем.

Вторая теорема предельного равновесия.

A. Система внешних нагрузок будет больше предельной, если существует кинематически допустимое поле скоростей деформации , для которого мощность внешних нагрузок больше, чем мощность / интенсивность / диссипации энергии в теле.

B. Коэффициент запаса n является наименьшим кинематически допустимым множителем, . Другими словами кинематически допустимый множитель является верхней оценкой коэффициента запаса.

Покажем эквивалентность обеих формулировок.

Пусть на тело действуют нагрузки не превышающие предельных. Пластическое течение впервые возникает при нагрузках . Пусть, далее, нагрузки , где - малое число перемещений обеспечивают неравенство . Тогда согласно формулировке А, нагрузки больше предельных откуда .

Доказательство.

Предположим, что действуют нагрузки и , не превосходящие предельные. Пластическое течение возникает при предельных нагрузках , . Предположим, что для нагрузок существует некоторое кинематически допустимое поле скоростей деформаций , для которого скорость диссипации механической энергии равна мощности внешних сил .

(1)

- напряжённое состояние, соответствующее течению по данному механизму .

Используем уравнение скорости виртуальных работ для действительных компонентов напряжений и компонент :

(2)

Вычитая из (1) (2), получим :

Здесь учтено, что .

Единственность распределения напряжений, соответствующих предельной нагрузке.

Пусть существуют два напряжённых состояния и , отвечающие одной предельной нагрузке. Пусть им соответствует некоторые скорости деформаций , .

Возникает вопрос о различии:

Составим уравнение виртуальных работ :

Вычитая эти равенства при одинаковых  и различных  получим :

Подъинтегральное выражение 0 (постулат Драккера ) ,т.е. подъинтегральное выражение =0.

Тогда :

1. Для строго выпуклой поверхности текучести в пластической зоне .

2. В той же части тела, которая остаётся упругой напряжённое состояние определено не однозначно.

3. Для невогнутой поверхности текучести вытекает, что и должны находиться на одной грани поверхности текучести.

Постановка задачи линейного программирования в теории предельного равновесия.

Пусть . Требуется найти максимум параметра при удовлетворении следующих условий :

Выполнение условий пластичности :

(может выражаться нелинейным образом)

Возможные нелинейные условия пластичности следует линеаризовывать, вводя кусочно-линейную аппроксимацию.

Для решения задач линейного программирования разработаны специальные методы, самым распространённым из которых является симплекс-метод. Пусть . Найти минимум параметра при удовлетворении следующих условий :