Лабораторная работа № 7 тарировка и определение метрологических характеристик тензометрической измерительной системы

1. Вводные сведения

Широкое распространение получили электрические системы измерения различных гидромеханических величин, построенные на мостовых схемах включения первичного преобразователя. Измеряемая величина, которую будем обозначать через , оказывает, как правило, механическое воздействие на первичный преобразователь, который переводит это воздействие в пропорциональное изменение активного, индуктивного или емкостного сопротивления электрическому току. Дальнейшая цепочка преобразований производится вторичной измерительной системой (тензостанцией) и заканчивается индикацией или записью выходного сигнала системы измерения, величину которого будем обозначать через I. Физически эта величина является напряжением или силой электрического тока в соответствующих единицах измерения.

Зависимость где выходной сигнал при =0 (условный ноль выхода, чаще всего называется тарировочной характеристикой. Она позволяет по индицируемому значению определить измеряемую величину .

Часто тарировочная характеристика определяется в форме зависимости от безразмерного приведенного выходного сигнала

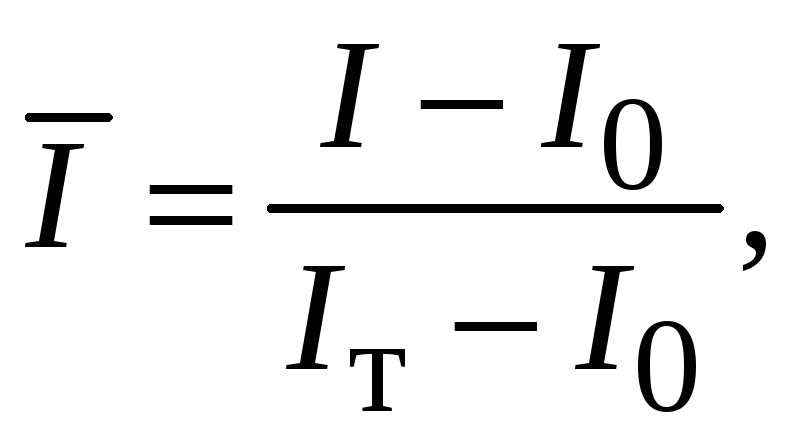(7.1)

где нормирующая величина, тарировочный сигнал, являющийся выходным сигналом при и при подачи на выход вторичной измерительной подсистемы высокостабильного электрического воздействия, имитирующего воздействие первичного преобразователя. Разность характеризует передаточное отношение вторичной подсистемы в данный момент времени так, что изменение этого отношения, произошедшее случайно или намеренно, например, путем переключения показывающего прибора (индикатора выходного сигнала) на другую чувствительность, не скажется на величине если остальные сигналы получены сразу же после , либо перед ним (более конкретно – см. подраздел 7.3). В дальнейшем под тарировочной характеристикой преимущественно будем понимать зависимость вида .

Определение тарировочной характеристики в заданной форме называется тарированием измерительной системы. Тарирование, чаще всего, производится путем подачи на вход системы ряда эталонных воздействий измеряемой величины (физическая природа этих воздействий может быть отличной от природы измеряемой величины). Фиксируются соответствующие значения выходного сигнала или , которые записанные в табличной форме вместе со значениями , образуют исходную тарировочную характеристику. Возможно ее непосредственное использование при определении измеряемой величины путем кусочно-линейной аппроксимации по точкам () (см. примечание 1). Но чаще используют графическую форму характеристики, получаемую путем соединения плавной линией точек (), нанесенных на график в соответствующих координатах (рис.7.1). Построение может производиться как вручную на миллиметровой бумаге, так и на компьютере.

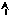
R

R_л

R,

R_л

0

Р

ис.7.1. Тарировочная характеристика и ее линейная аппроксимация

Если зависимость достаточно близка к линейной, то целесообразно использовать ее линейную аппроксимацию

, (7.2)

где М – коэффициент пропорциональности, называемый масштабом. При получим и , т.е. величина масштаба приближенно равна определенному значению измеряемой величины R, воздействие которой индуцирует на выходе сигнал .

Если результат измерения определяется по (7.2) как значение , то образуется погрешность нелинейности , где – значение по исходной тарировочной характеристике в графической или табличной форме.

Максимальная в рабочем диапазоне измерений погрешность нелинейности (см. рис. 7.1) сравнивается с пределом основной погрешности системы измерения в данном диапазоне измерений (относительно величины см. п. 7.1.4). Если существенно больше значения , то использовать линейную зависимость (7.2) не рекомендуется.

Если значение пренебрежимо мало по сравнению с , то тарировочная характеристика совпадает с зависимостью (7.2), которая и рекомендуется к использованию. При этом процесс тарирования может быть сокращен до определения масштаба М по одной экспериментальной точке (). Дополнительные преимущества использования зависимости (7.2), а также наиболее прогрессивный способ тарирования приводятся в примечании 2. Если величина сравнима с , то возможно ограниченное использование линейной зависимости (7.2) с определением масштаба по исходной тарировочной характеристике из условия минимизации погрешности нелинейности (см. рис. 7.1). Для решения отмеченных вопросов необходимо определение соответствующих метрологических характеристик измерительной системы (см. п.п. 7.1.2 – 7.1.5).

Примечание 1. Кусочно-линейная аппроксимация по тарировочным точкам () используется тогда, когда имеется существенная нелинейность зависимости , но точки () расположены на ней достаточно часто и ее участки между данными точками с пренебрежимо малой погрешностью аппроксимируются линейными зависимостями , где

При использовании этих зависимостей не требуется графическое изображение характеристики, что позволяет производить соответствующее тарирование достаточно часто, в пределе после или перед каждым измерением величины R. Это повышает точность измерений, а также позволяет отказаться от использования тарировочного сигнала и при точной установке нуля () перейти к зависимости R от физической величины I выходного сигнала.

Примечание 2. Перед измерениями выходной сигнал I принято устанавливать на нулевое значение (). Однако, настройка на точное значение требует наличия в системе соответствующих элементов точной настройки. Если их нет, то линейный характер зависимости (7.2) позволяет ограничиться грубой настройкой и использовать произвольное значение , которое и называется условным нулем. Причем, при повторных измерениях настройку можно не производить, а просто измерять выходной сигнал при R = 0, что особенно удобно при автоматизированном эксперименте и необходимо в случае наличия у системы измерения существенного дрейфа нуля (в этом случае определение производится два раза – перед измерением величины R и после него, затем в качестве используется среднеарифметическое этих двух значений).

Отметим, что тензометрические системы часто используются для измерения роста или уменьшения величины R воздействия на первичный преобразователь от некоторого первоначального значения . Часто это первоначальное воздействие связано с весом различных механических элементов механоэлектрического преобразователя, переводящего механическое воздействие R в электрический сигнал. При измерениях повышения давления на фронте ударной волны, например, во время гидравлического удара в трубах связано с воздействием на мембрану, первоначального гидростатического давления перед фронтом ударной волны. Можно привести множество других примеров наличия первоначального воздействия.

Очевидно значение должно определяться при начальном воздействии , . Данное условие выполняется как при построении тарировочной характеристики, так и при последующих измерениях. Точка является условным нулем системы измерения. Причем, значение может оставаться неизвестным.

В случае, если тарировочная характеристика обладает существенной нелинейностью, воздействие и сигнал должны быть строго постоянными. Это не всегда удобно, например, нежелателен перевод первичного преобразователя во время тарировки из горизонтального положения в вертикальное с целью использования в качестве эталонного силового воздействия веса аналитических гирь, так как к этому весу добавится собственный вес определенных элементов первичного преобразователя (см. подраздел 7.3).

Этого недостатка нет, если зависимость между линейная – . Действительно, при любом условном нуле (,) из диапазона измерения система с линейной тарировочной характеристикой обеспечивает пропорциональность изменения входного воздействия и выходного сигнала Проинтегрировав левую часть данного равенства от до , а правую, соответственно, от до , получим

. (7.3)

Значения в (7.3) могут быть произвольными, так как коэффициент К от них не зависит. Аналогично при имитационном (электрическом) тарировочном воздействии

(7.4)

Как отмечалось, это воздействие, называемое масштабом (), более стабильно, чем коэффициент , и также, как , не зависит от . Из (7.3) и (7.4) получим

где измеряемая величина не зависит от условного нуля. Причем, этот ноль в (7.3) и в (7.4), а также при тарировке с целью определения масштаба может быть различным.

Если тарировочная характеристика нелинейная, то коэффициент К в (7.3) и (7.4) зависит от значений условного нуля. Отклонение этих значений во время измерений от условного нуля при тарировке является источником дополнительной погрешности измерения, максимальное значение которой при использовании (7.2) равно максимальной погрешности нелинейности и добавляется к последней.

Однако, если данное отклонение мало по сравнению с частью диапазона измерения, на которой образуется (см. рис. 7.1), то и эта дополнительная погрешность будет мала по сравнению с . В настоящей работе данное соотношение считается выполненным, и указанным дополнительным источником погрешности пренебрегаем.

Использование зависимости (7.2) при наличии линейной характеристики повышает точность измерений за счет более высокой стабильности имитационного воздействия по сравнению с коэффициентом (см. подраздел 7.3). Однако, появляется недостаток, связанный с необходимостью соответствующих расчетов. В этой связи отметим, что существует более удобный способ использования имитационного воздействия . Он заключается в том, что при подаче данного воздействия путем варьирования передаточным отношением вторичной измерительной подсистемы выставляется значение выходного сигнала, численно равное . Зависимость превращается при этом в зависимость в определенных единицах измерения, т.е. с индикатора непосредственно снимается измеряемая величина . Данный метод используется, например, в измерительных комплексах ИПДЦ (измерительный преобразователь давления цифровой). Но для универсальных тензостанций, предназначенных для работы с различными датчиками различных величин в очень широком диапазоне измерений, этот метод трудно осуществим и в настоящей работе не используется.

2. Ниже приводится метод определения масштаба зависимости (7.2) и максимальной нелинейности тарировочной характеристики.

Как отмечалось в п. (7.1.1), тарировочная характеристика в общем случае нелинейна и определяется рядом экспериментальных точек (), – число этих точек, возрастающий ряд эталонных воздействий, имитирующих измеряемую величину – соответствующий, приведенный по (7.1), выходной сигнал. Число точек берется, как правило, не менее 8÷10. Последнее значение равно назначенному пределу измерений. Начальная точка характеристики включается в диапазон измерений по самому определению зависимости (1.2), т.е. общее число точек . Ряд значений заполняет диапазон измерений равномерно.

Возможен последовательный план тарировки, когда подаваемые воздействия следуют в возрастающем, или убывающем порядке, и рандамизированный план, когда эти воздействия следуют в случайном порядке. Последний применяют в случае обнаружения зависимости от времени выходного сигнала для одного и того же воздействия . Тогда случайный выбор величины этого воздействия снижает негативное влияние данной зависимости на точность определения масштаба. Очевидно, если при тарировании используется рандамизированный план, то и измерения при использовании системы целесообразно проводить по такому же плану. Отметим, что зависимость от времени выходного сигнала может существовать по многим причинам. Обычно рассматривается монотонная зависимость, иногда называемая трендом показаний. Наиболее часто встречаемая его причина связана с постепенным прогревом работающей установки (рекомендуется приступать к работе на тензостанции после 30-45 минут ее прогрева). Другая причина, специфическая для измерений в области гидромеханики и гидравлических машин, может быть связана с постепенным изменением влажности воздуха под воздействием перемещаемых масс воды на работающей установке. Разумеется надежная изоляция электрических элементов предотвращает подобное, но остается вопрос, насколько она надежна.

Тарировочная характеристика будет построена точнее, если тарировка по ряду значений производится несколько раз, а затем используются среднеарифметические значения выходного сигнала

(7.5)

где - число повторов, - приведенное значение выходного сигнала для -го повтора воздействия .

Для определения масштаба и погрешности нелинейности исходную тарировочную характеристику целесообразно представить в графической форме. Чаще всего она имеет два экстремума погрешности нелинейности – в центре ) и в конце ) – см. рис. 7.1. Очевидно, условие минимизации максимальной погрешности при определении линейной аппроксимационной зависимости (7.2) сводится к равенству

(7.6)

По условию (7.6) зависимость (7.2) определяется фактически по двум точкам исходной тарировочной характеристики с максимальными отклонениями от линейности и . Обозначим значения и в этих точках , соответственно (рис. 1.1). Аппроксимационные значения в этих точках равны Перепишем (7.6) в следующем виде:

.

Отсюда получим выражение для определения масштаба

. (7.7)

При этом отсутствует графическая погрешность, возникающая в случае определения каких-либо значений по графику.

Максимальная нелинейность () тарировочной характеристики в процентах от предела измерений равна

(7.9)

где - предел измерения, совпадающий с максимальным эталонным воздействием.

Выражение (7.8) с определенной достоверностью характеризует действительную погрешность нелинейности при назначенном масштабе только тогда, когда доверительная погрешность правой части (7.8) существенно (по крайней мере в два раза) меньше расчетного по (7.8) значения . Это требование эквивалентно тому, что при условии пренебрежимо малых погрешностей эталонных воздействий и при условии достаточно большого числа повторных измерений при тарировании (по крайней мере ) погрешность нелинейности по (7.8) не меньше предела основной погрешности системы измерения , т.е. (обоснование данного положения см. в примечании 3).

Определенная с достаточной достоверностью, погрешность нелинейности учитывается как добавочная погрешность измерения путем арифметического сложения с , если используется линейная аппроксимация (7.2). Погрешность рассматривается как предельное с заданной доверительной вероятностью отклонение, измеренного и определенного по исходной нелинейной тарировочной характеристике (в табличной или графической формах), воздействия от его действительного значения.

В противном случае (при указанных выше условиях в случае ) за исходную тарировочную характеристику принимается линейная аппроксимация (1.2) (в п. 7.1.1 данный случай отмечается как вариант строго линейной характеристики). Погрешность нелинейности включается в предел основной погрешности системы измерения, которая рассматривается как предельное с заданной доверительной вероятностью отклонение (), где определяется по (7.2), и которую для отличия от предыдущего случая обозначим через . Отметим также, что в данном случае аппрксимационную зависимость (7.2) и масштабом целесообразно определять методом наименьших квадратов.

Примечание 3. Определим относительную доверительную погрешность величины , вычисляемый по формуле (7.8) при условиях , погрешности эталонных воздействий пренебрежимо малы, , функции распределения вероятностей для всех погрешностей являются нормальными. Из (7.8) и (7.7) получим следующее выражение

.

Имеем следующую функцию двух случайных величин (погрешностями пренебрегаем):

Общее выражение для определения половины ширины доверительного интервала функции двух случайных величин имеет следующий вид:

, (7.10)

где - половинки ширины доверительных интервалов неопределенности данных случайных величин.

В рассматриваемом случае под величинами следует понимать искомую доверительную погрешность и доверительные погрешности значений исходной тарировочной характеристики.

Для производных в (1.10) имеем

С учетом (7.7) из (7.10) получим

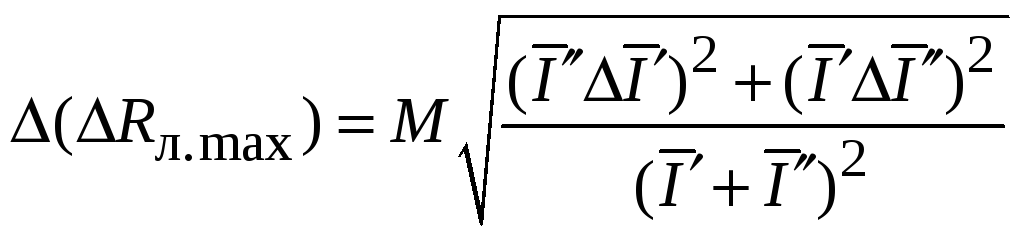. (7.11)

Отметим, очевидные соотношения , где предел погрешности тарирования, приведенный к выходу системы измерения и определяемый как максимальная доверительная погрешность по ряду значений исходной тарировочной характеристики. Как показано в (7.1.3), данная погрешность связана с пределом основной погрешности измерения соотношением В результате из (7.11) получим

С учетом условий и использовав неравенство <, будем иметь

.

Данная точность достаточна для принятия качественного решения о форме использования исходной тарировочной характеристики по п. 7.1.1.

2. Ниже рассматривается доверительная погрешность тарирования тензометрической измерительной системы. Ее источниками являются доверительные погрешности 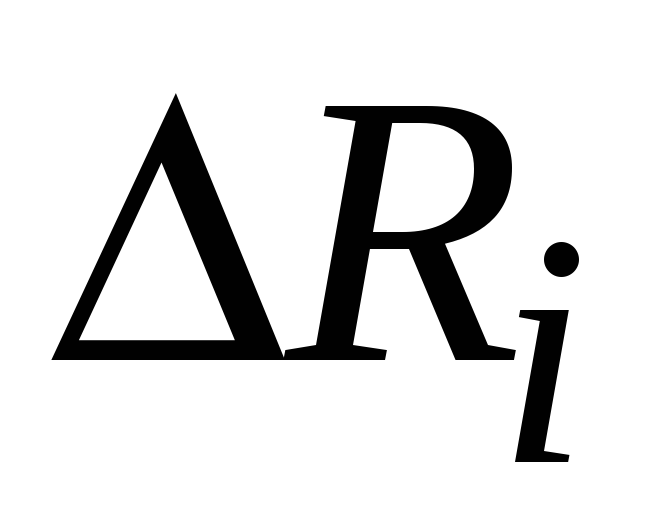используемых эталонных воздействий и стохастический разброс приведенного выходного сигнала возникающий при повторных воздействиях ( одной и той же входной величины в определенных условиях тарирования, принятых за номинальные условия измерения.

Данный разброс определяется как отклонение от математического ожидания величины при номинальных условиях измерения. Его среднеквадратичное значение в квадрате, получаемое как предел при бесконечно большом числе повторных измерений называется дисперсией воспроизводимости. Соответствующая доверительная погрешность выходного сигнала, которую обозначим через является половиной ширины интервала неопределенности, в который значение попадает с заданной вероятностью, называемой доверительной.

Значение является центром данного интервала. Среднеарифметическое значение , получаемое по формуле (7.5), является оценкой величины . Отклонение этой оценки от действительного значения характеризуется своей дисперсией воспроизводимости и своей доверительной погрешностью, которую обозначим через .

По центральной теореме статистики дисперсия воспроизводимости среднеарифметического значения в раз меньше дисперсии воспроизводимости сигнала . Причем, погрешности для тензометрических систем обычно рассматриваются как случайные величины с нормальной (Гаусовской) функцией распределения вероятностей. Исходя из этого, можно записать

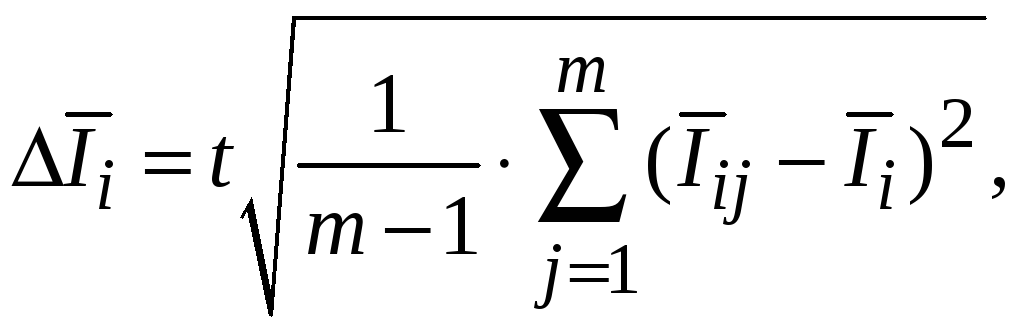(7.12)

(7.13)

где – коэффициент Стьюдента (см. лаб. раб. №1).

Погрешности являются погрешностями определения точек исходной тарировочной характеристики по соответствующим координатам. Суммарное доверительное отклонение () по координате исходной тарировочной характеристики от действительной (истинной) характеристики в окрестности точки в общем случае равно

(7.14)

где - производная функции в данной точке.

Максимальная по всем значениям величина является пределом погрешности тарировки для исходной тарировочной характеристики, приведенным ко входу измерительной системы, т.е. определяемым по координате зависимости Иногда более удобно использовать предел погрешности тарировки , приведенный к выходу системы измерения, т.е. определенный по координате обратной зависимости

Обычно погрешность эталонного воздействия мала и ею можно пренебречь. Тарировочная характеристика в данной работе достаточно близка к линейной и можно принять Тогда из (7.14) и (7.13) получим

(7.15)

где – максимальное значение доверительной погрешности по всему ряду измерений.

Для предела погрешности тарировки будем иметь следующую зависимость

(7.16)

Точность тарировки охарактеризуем пределом приведенной погрешности в процентах от предела измерения, который совпадает в данной работе со значением для для .

По (7.15) и (7.16) с учетом запишем

(7.17)

Данные равенства показывают одно из свойств линейной характеристики, заключающееся в том, что величина приведенной погрешности не зависит от того, по какой координате характеристики эта погрешность берется.

Точность определения аппроксимации (7.2) тарировочной характеристики оценивается доверительной приведенной погрешностью масштаба

(7.18)

где – доверительная погрешность .

В соответствии с формулой (7.7), пренебрегая погрешностями эталонных воздействий, запишем

(7.19)

где, - доверительные погрешности величин (см. п. 7.1.2), равные соответствующим значениям по (7.13). Из (7.19) и (7.18) легко получить следующее выражение:

(7.20)

2. Точность тензометрической измерительной системы характеризуется прежде всего пределом основной – приведенной погрешности системы измерения . В данной работе под пределом основной погрешности системы измерений понимается максимальная в диапазоне измерений доверительная погрешность измерения, выполняемого в условиях, соответствующих нормальным условиям тарировки, с использованием исходной тарировочной характеристики (см. п.7.1.2).

Источниками погрешности являются дисперсия воспроизводимости выходного сигнала с соответствующей ей по формуле (7.12) доверительной погрешностью (учитывается максимальное значение в диапазоне измерений), а также погрешность тарировки , характеризующая точность используемой исходной тарировочной характеристики по координате (см. п. 7.1.3). Общее выражение для суммирования этих погрешностей запишется в следующем виде:

, (7.22)

где - производная зависимости С учетом (7.15), (7.21) и соотношения получим

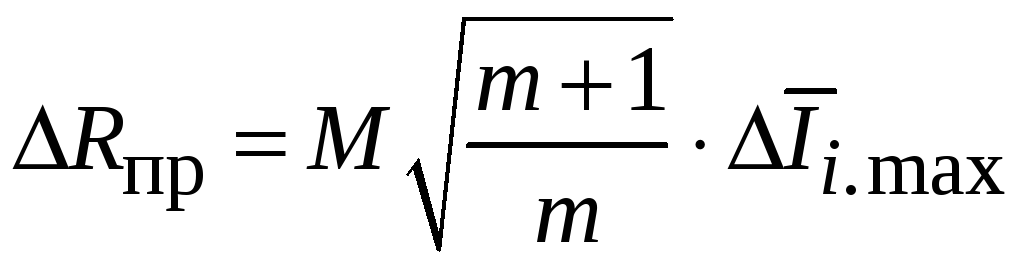, (7.23)

(7.24)

При использовании линейной аппроксимации (7.2) возникает добавочная погрешность нелинейности . В случае, если она определена с достаточной степенью достоверности, то предел основной погрешности измерения (обозначим его через ) в соответствии с замечанием, сделанным в п. 7.1.2 следует определить по следующей формуле:

. (7.25)

В противном случае величина мала и ее следует учесть при расчете основной погрешности путем замены в (7.12) значений на модельные величины . При этом .

7.1.5. При отличии условий измерения от нормальных условий тарировки возникают дополнительные погрешности, определить значение такой погрешности можно по формуле:

, (7.26)

где - среднеарифметические значения приведенного выходного сигнала, полученные для ряда эталонных воздействий , соответственно, в нормальных условиях и в условиях существенно отличающихся от нормальных, но возможных при эксплуатации измерительной системы.

Значение исследуется по величине и характеру влияния различных факторов, определяющих условия работы измерительной системы. В данной работе проводится исследование влияния лишь одного наиболее важного фактора – водо-воздушного режима работы экспериментальной установки (см. подраздел 7.3). Наиболее простой и надежный способ учета дополнительной погрешности измерения как составляющей предела погрешности измерения производится по формуле

, (7.27)

где – максимальное обнаруженное значение . Недостаток этого способа заключается в существенном росте величины .

Более точен способ, по которому значение учитывается как поправка к результату измерения. Но соответствующие исследования значения выходят за рамки данной работы из-за их сложности.

Отметим, что в данной работе рассматриваются предел основной погрешности системы измерения, включающий погрешности, зависящие только от самой системы и исходной тарировочной характеристики, предел основной погрешности измерения, дополнительно включающий погрешность, нелинейности характеристики при использовании ее линейной апроксимации, и предел погрешности измерения, добавочно включающий дополнительные погрешности.

Примечание 4. Ниже рассмотрена цифровая погрешность округления () выходного сигнала и графическая погрешность () считывания показаний с исходной тарировочной характеристики в графической форме. В данной работе используется цифровой индикатор выходного сигнала. При измерениях воздействия , связанного с какими-либо гидромеханическими процессами, это воздействие обычно содержит пульсационную стохастическую составляющую (часто она определяется турбулентными пульсациями скорости и давления потока жидкости). При определении выходного сигнала для такого пульсационного воздействия показания младших разрядов цифрового индикатора могут оказаться нестабильными. Тогда учитываются только те разряды сигнала, значения которых достаточно стабильны (либо постоянны, либо очевидным образом превалируют над редкими отклонениями). Обозначим единичное значение младшего из учитываемых разрядов через .

Очевидно, ширина интервала неопределенности, отбрасываемых при округлении величин, равна . Округленное значение на числовой оси модуля выходного сигнала является нижней границей данного интервала. Центр последнего, т.е. значение

(7.28)

следует принять в качестве наиболее правдоподобной оценки выходного сигнала. Причем, доверительная погрешность округления по (7.27) равна (половине ширины интервала). Соответствующая доверительная погрешность округления приведенного по (7.1) выходного сигнала равна

Возможны две формы записи выходного сигнала . Первая из них – запись с поправкой по (7.28). Тогда по правилам учета погрешности с равномерной плотностью распределения для предела погрешности измерения вместо (7.27) приближенно можно записать

. (7.29)

Вторая форма записи является упрощенной. Принимается , а поправка по (7.28) - в приведенном виде, равная , добавляется арифметически, как детерминированное значение.

В результате получим

. (7.30)

Отметим, что значение в (7.29) и (7.30) определяется по максимальной величине в диапазоне измерения (как правило, при ).

При использовании исходной тарировочной характеристики в графической форме для определения воздействия по измеренному выходному сигналу образуются случайные графические погрешности, как по оси , так и по оси графика. Обозначим соответствующий предельный размер линейного отклонения через . Для графика на миллиметровой бумаге можно принять =0,5 мм. Отметим, что значения , используемые при тарировке, целочисленны и соответствуют линиям миллиметровой бумаги графика. Поэтому отклонение по оси проявляется только один раз – при считывании определяемой величины с графика. По оси отклонение проявляется два раза – при нанесении графика на миллиметровую бумагу после тарировки и при считывании величины с графика по измеренному сигналу .

Исходя из этого, итоговую доверительную графическую по погрешность величины и ее приведенное значение по пределу измерения можно определить как сумму приведенных значений предельных отклонений по осям и графика по следующей формуле:

, (7.31)

где ходя из этого, итоговую доверительную графическу. ровки и при считывании величины аги графика. ствия 0000000000000000000000000, - размеры графика по осям , ограниченные пределами измерений .

Погрешность следует отнести как добавочную к пределу основной погрешности системы измерения . Рекомендуется при построении графика исходной тарировочной характеристики выбирать его размеры такими достаточно большими, чтобы выполнялось . Тогда графической погрешностью можно пренебречь.