
- •Лабораторная работа № 7 тарировка и определение метрологических характеристик тензометрической измерительной системы
- •7.3. Описание установки и тензометрической системы измерения
- •2 1 3 4 6 5 R
- •7.5. Обработка данных тарировки
- •7.6. Анализ результатов
- •П 7.2. Взаимосвязь погрешностей, приведенных ко входу и выходу системы измерения
- •П 7.3. Уточненный расчет предела погрешности по ее случайным и детерминированным систематическим составляющим
- •П 7.4. Погрешности округления выходного сигнала и считывания показаний с графика
- •П 7.5. Электрическая схема измерений
Лабораторная работа № 7 тарировка и определение метрологических характеристик тензометрической измерительной системы
Вводные сведения
Широкое распространение
получили электрические системы измерения
различных гидромеханических величин,
построенные на мостовых схемах включения
первичного преобразователя. Измеряемая
величина, которую будем обозначать
через
![]() ,
оказывает, как правило, механическое
воздействие на первичный преобразователь,
который переводит это воздействие в
пропорциональное изменение активного,
индуктивного или емкостного сопротивления
электрическому току. Дальнейшая цепочка
преобразований производится вторичной
измерительной системой (тензостанцией)
и заканчивается индикацией или записью
выходного сигнала системы измерения,
величину которого будем обозначать
черезI.
Физически эта величина является
напряжением или силой электрического
тока в соответствующих единицах
измерения.
,
оказывает, как правило, механическое
воздействие на первичный преобразователь,
который переводит это воздействие в
пропорциональное изменение активного,
индуктивного или емкостного сопротивления
электрическому току. Дальнейшая цепочка
преобразований производится вторичной
измерительной системой (тензостанцией)
и заканчивается индикацией или записью
выходного сигнала системы измерения,
величину которого будем обозначать
черезI.
Физически эта величина является
напряжением или силой электрического
тока в соответствующих единицах
измерения.
Зависимость
![]() где
где![]() — выходной сигнал при
— выходной сигнал при![]() = 0
(условный ноль выхода, чаще всего
= 0
(условный ноль выхода, чаще всего![]() называется тарировочной характеристикой.
Она позволяет по индицируемому значению
называется тарировочной характеристикой.
Она позволяет по индицируемому значению![]() определить измеряемую величину
определить измеряемую величину![]() .
.
Часто тарировочная
характеристика определяется в форме
зависимости
![]() от безразмерного приведенного выходного
сигнала:
от безразмерного приведенного выходного
сигнала:
 (7.1)
(7.1)
где
![]() — нормирующая величина;
— нормирующая величина;![]() — тарировочный сигнал, являющийся
выходным сигналом при
— тарировочный сигнал, являющийся
выходным сигналом при![]() и при подаче на вход вторичной измерительной
подсистемы высокостабильного
электрического воздействия, имитирующего
воздействие первичного преобразователя.
Разность
и при подаче на вход вторичной измерительной
подсистемы высокостабильного
электрического воздействия, имитирующего
воздействие первичного преобразователя.
Разность![]() характеризует передаточное отношение
вторичной подсистемы в данный момент
времени. Изменение этого отношения,
произошедшее за пределами процесса
измерения вследствие, например, колебаний
температуры окружающей среды, не скажется
на величине
характеризует передаточное отношение
вторичной подсистемы в данный момент
времени. Изменение этого отношения,
произошедшее за пределами процесса
измерения вследствие, например, колебаний
температуры окружающей среды, не скажется
на величине![]() (более конкретно – см. § 7.3). В дальнейшем
под тарировочной характеристикой будем
понимать зависимость вида
(более конкретно – см. § 7.3). В дальнейшем
под тарировочной характеристикой будем
понимать зависимость вида![]() .
.
Определение
тарировочной характеристики в заданной
форме называется тарированием
измерительной системы. Чаще всего оно
производится путем подачи на вход
системы ряда эталонных воздействий
![]() измеряемой величины
измеряемой величины![]() (физическая природа этих воздействий
может быть отличной от природы измеряемой
величины). Фиксируются соответствующие
значения выходного сигнала
(физическая природа этих воздействий
может быть отличной от природы измеряемой
величины). Фиксируются соответствующие
значения выходного сигнала![]() или
или![]() ,
которые, записанные в табличной форме
вместе со значениями
,
которые, записанные в табличной форме
вместе со значениями![]() ,
образуют исходную тарировочную
характеристику. Возможно ее непосредственное
использование при определении измеряемой
величины
,
образуют исходную тарировочную
характеристику. Возможно ее непосредственное
использование при определении измеряемой
величины![]() путем кусочно-линейной аппроксимации
по точкам (
путем кусочно-линейной аппроксимации
по точкам (![]() )
(см. примечание 1). Но чаще используют
графическую форму характеристики,
получаемую путем соединения плавной
линией точек (
)
(см. примечание 1). Но чаще используют
графическую форму характеристики,
получаемую путем соединения плавной
линией точек (![]() ),
нанесенных на график в соответствующих
координатах (рис.7.1).
),
нанесенных на график в соответствующих
координатах (рис.7.1).
R
Rл R,
Rл
0
![]()





![]()
![]()
![]()
![]()







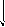






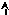
Рис.7.1. Тарировочная характеристика и ее линейная аппроксимация
Если зависимость
![]() достаточно близка к линейной, то
целесообразно использовать ее в форме
линейной аппроксимации
достаточно близка к линейной, то
целесообразно использовать ее в форме
линейной аппроксимации
![]() ,
(7.2)
,
(7.2)
где М — коэффициент пропорциональности, называемый масштабом.
Если результат
измерения определяется по (7.2) как
значение
![]() ,
то образуется погрешность нелинейности
,
то образуется погрешность нелинейности![]() ,
где
,
где![]() — значение по исходной тарировочной
характеристике в графической или
табличной форме.
— значение по исходной тарировочной
характеристике в графической или
табличной форме.
Максимальная в
рабочем диапазоне измерений погрешность
нелинейности
![]() (см. рис. 7.1) сравнивается с пределом
основной погрешности системы измерения
(см. рис. 7.1) сравнивается с пределом
основной погрешности системы измерения![]() ,
который характеризует точность этой
системы вне зависимости от формы
использования тарировочной характеристики
и условий измерения (подробнее о величине
,
который характеризует точность этой
системы вне зависимости от формы
использования тарировочной характеристики
и условий измерения (подробнее о величине![]() см. пп. 7.1.3). Сравнение производится
также с пределом погрешности измерения
см. пп. 7.1.3). Сравнение производится
также с пределом погрешности измерения![]() ,
учитывающим все составляющие погрешности
измерения, производимого с использованием
тарировочной характеристики в табличной
форме (см. пп. 7.1.6).
,
учитывающим все составляющие погрешности
измерения, производимого с использованием
тарировочной характеристики в табличной
форме (см. пп. 7.1.6).
Если значение
![]() пренебрежимо мало по сравнению с
пренебрежимо мало по сравнению с![]() (ориентировочно
(ориентировочно![]() ≤ 0,4
≤ 0,4![]() ),
то тарировочную характеристику можно
считать строго линейной, совпадающей
с зависимостью (7.2). При этом процесс
тарирования может быть сокращен до
определения масштабаМ
по одной экспериментальной точке,
соответствующей пределу измерения (
),
то тарировочную характеристику можно
считать строго линейной, совпадающей
с зависимостью (7.2). При этом процесс
тарирования может быть сокращен до
определения масштабаМ
по одной экспериментальной точке,
соответствующей пределу измерения (![]() в данной работе). При наличии ряда
экспериментальных точек масштабM
целесообразно
определять по этому ряду методом
наименьших квадратов.
в данной работе). При наличии ряда
экспериментальных точек масштабM
целесообразно
определять по этому ряду методом
наименьших квадратов.
Дополнительные
преимущества использования зависимости
(7.2) приводятся в прилож. П 7.1. Ввиду
этих преимуществ зависимость (7.2) часто
используют и в том случае, когда величина
![]() сравнима с
сравнима с![]() .
При этом предел погрешности измерения
возрастает на величину
.
При этом предел погрешности измерения
возрастает на величину![]() .
Поэтому масштаб рекомендуется определять
по исходной тарировочной характеристике
из условия минимизации погрешности
нелинейности
.
Поэтому масштаб рекомендуется определять
по исходной тарировочной характеристике
из условия минимизации погрешности
нелинейности![]() (см.
рис. 7.1). В этом случае тарировочную
характеристику будем называть условно
линейной.
(см.
рис. 7.1). В этом случае тарировочную
характеристику будем называть условно
линейной.
Если значение
![]() существенно больше погрешности
существенно больше погрешности![]() ,
либо
,
либо![]() ≥
≥![]() ,
то использовать линейную зависимость
(7.2) не рекомендуется. Тарировочную
характеристику в этом случае будем
называть нелинейной.
,
то использовать линейную зависимость
(7.2) не рекомендуется. Тарировочную
характеристику в этом случае будем
называть нелинейной.
Точность тарировки
не всегда достаточна для обоснованного
разграничения вида характеристики на
строго и условно линейную. В этом случае
рекомендуется дополнительно учесть
характер отклонений ряда экспериментальных
точек (![]() )
от линейной аппроксимации (7.2). Эти
отклонения по ходу строго линейной
характеристики носят четко выраженный
стохастический характер. Наоборот, для
условно линейной характеристики
присутствует определенная закономерность
типа закономерности, показанной на
рис. 7.1.
)
от линейной аппроксимации (7.2). Эти
отклонения по ходу строго линейной
характеристики носят четко выраженный
стохастический характер. Наоборот, для
условно линейной характеристики
присутствует определенная закономерность
типа закономерности, показанной на
рис. 7.1.
Примечание 1.Кусочно-линейная
аппроксимация по тарировочным точкам
(![]() )
используется тогда, когда имеется
существенная нелинейность зависимости
)
используется тогда, когда имеется
существенная нелинейность зависимости
![]() ,
но точки (
,
но точки (![]() )
расположены на ней достаточно часто и
ее участки между данными точками с
пренебрежимо малой погрешностью
аппроксимируются линейными зависимостями
)
расположены на ней достаточно часто и
ее участки между данными точками с
пренебрежимо малой погрешностью
аппроксимируются линейными зависимостями
![]() ,
где
,
где![]()
Ниже приводится метод определения масштаба
 зависимости (7.2) и максимальной
нелинейности тарировочной характеристики.
зависимости (7.2) и максимальной
нелинейности тарировочной характеристики.
Как отмечалось в
пп. 7.1.1, тарировочная характеристика в
общем случае не является линейной и
определяется рядом экспериментальных
точек (![]() ),
),![]() — число этих точек;
— число этих точек;![]() — возрастающий ряд эталонных воздействий,
имитирующих измеряемую величинуR;
— возрастающий ряд эталонных воздействий,
имитирующих измеряемую величинуR;
![]() — соответствующий приведенный выходной
сигнал. Число
— соответствующий приведенный выходной
сигнал. Число![]() точек берется, как правило, не менее
8÷10. Последнее значение
точек берется, как правило, не менее
8÷10. Последнее значение![]() равно назначенному пределу измерений.
Начальная точка характеристики
равно назначенному пределу измерений.
Начальная точка характеристики![]() включается в диапазон измерений по
самому определению зависимости (1.2),
т.е. общее число точек равно
включается в диапазон измерений по
самому определению зависимости (1.2),
т.е. общее число точек равно![]() .
Ряд значений
.
Ряд значений![]() заполняет диапазон измерений равномерно.
заполняет диапазон измерений равномерно.
Тарировочная
характеристика будет построена точнее,
если тарировка по ряду значений
![]() производится несколько раз, а затем
используются среднеарифметические
значения выходного сигнала:
производится несколько раз, а затем
используются среднеарифметические
значения выходного сигнала:
 (7.3)
(7.3)
где
![]() — число повторов;
— число повторов;![]() — приведенное по (7.1) значение выходного
сигнала для
— приведенное по (7.1) значение выходного
сигнала для![]() -го
повтора воздействия
-го
повтора воздействия![]() .
.
Для определения
масштаба и погрешности нелинейности
исходную тарировочную характеристику
целесообразно представить в графической
форме. Чаще всего она имеет два экстремума
погрешности нелинейности – в центре
графика
![]() и в его конце
и в его конце![]() (см. рис. 7.1). Условие минимизации
максимальной погрешности нелинейности,
необходимость использования которого
обоснована в пп. 7.1.1, сводится к равенству
(см. рис. 7.1). Условие минимизации
максимальной погрешности нелинейности,
необходимость использования которого
обоснована в пп. 7.1.1, сводится к равенству
![]() .
(7.4)
.
(7.4)
По условию (7.4)
зависимость (7.2) определяется фактически
по двум точкам исходной тарировочной
характеристики с максимальными
отклонениями от линейности
![]() и
и![]() .
Обозначим значенияR
и
.
Обозначим значенияR
и
![]() в этих точках через
в этих точках через![]() соответственно (см. рис. 7.1). Аппроксимационные
значения
соответственно (см. рис. 7.1). Аппроксимационные
значения![]() в этих точках равны
в этих точках равны![]() Перепишем (7.4) в следующем виде:
Перепишем (7.4) в следующем виде:![]() .
.
Отсюда получим выражение для определения масштаба:
![]() .
(7.5)
.
(7.5)
Данные для формулы
(7.5) целесообразно брать непосредственно
по исходной тарировочной характеристике
в табличной форме, использовав ее
графическую форму (см. рис. 7.1) для
предварительного определения номеров
(i)
точек, соответствующих максимальнойпогрешности
нелинейности ![]() .
Последнюю,зная
масштаб,можно
определить по следующей формуле:
.
Последнюю,зная
масштаб,можно
определить по следующей формуле:
![]() (7.6)
(7.6)
При этом отсутствует графическая погрешность, возникающая в случае определения каких-либо значений по графику.
Максимальная
нелинейность (![]() )
тарировочной характеристики в процентах
от предела измерений, который в данной
работе совпадает с максимальным эталонным
воздействием
)
тарировочной характеристики в процентах
от предела измерений, который в данной
работе совпадает с максимальным эталонным
воздействием![]() ,
равна
,
равна
 .
(7.7)
.
(7.7)
Если воздействия
![]() определены с достаточной достоверностью,
то процесс тарирования при дальнейшей
эксплуатации системы с условно линейной
характеристикой может быть сокращен
до определения величин
определены с достаточной достоверностью,
то процесс тарирования при дальнейшей
эксплуатации системы с условно линейной
характеристикой может быть сокращен
до определения величин![]() и масштабаM
по формуле
(7.5). Такая тарировка менее трудоемка и
может производиться более часто с целью
снижения прогрессирующей и дополнительной
температурной погрешностей.
и масштабаM
по формуле
(7.5). Такая тарировка менее трудоемка и
может производиться более часто с целью
снижения прогрессирующей и дополнительной
температурной погрешностей.
Достоверность
оценки величины
![]() и определения воздействий
и определения воздействий![]() может быть установлена качественно по
зависимости отR
отклонения
может быть установлена качественно по
зависимости отR
отклонения
![]() тарировочной характеристики. Данная
зависимость в достаточно больших
диапазонах справа и слева от значения
тарировочной характеристики. Данная
зависимость в достаточно больших
диапазонах справа и слева от значения![]() ,
а также справа и слева от значения
,
а также справа и слева от значения![]() должна быть монотонной (см. рис. 7.1). В
настоящей работе эти диапазоны кроме
точек
должна быть монотонной (см. рис. 7.1). В
настоящей работе эти диапазоны кроме
точек![]() должны включать еще минимум по две
экспериментальные точки (диапазон
справа от
должны включать еще минимум по две
экспериментальные точки (диапазон
справа от![]() отсутствует).
отсутствует).
7.1.3. Ниже
рассматривается основная погрешность
системы измерения. На результат измерения
оказывает влияние совокупность условий,
при которых это измерение производится
(температура воды, температура и влажность
окружающего воздуха и т. д.). Условия,
при которых произведена тарировка,
принимаются, как правило, за нормальные
условия измерения.
Погрешности измерений в нормальных
условиях называются основными. Ряд
значений
![]() (
(![]() )
выходного сигнала, полученный при
повторных воздействиях одной и той же
входной величины
)
выходного сигнала, полученный при
повторных воздействиях одной и той же
входной величины![]() в нормальных условиях измерения, имеет
определенный стохастический разброс.
Соответствующая дисперсия называетсядисперсией
воспроизводимости.
Она определяет точность системы как ее
внутреннее свойство, не зависящее от
характера тарировки, формы используемой
тарировочной характеристики и условий
измерения. Соответствующую доверительную
погрешность можно назвать основной
погрешностью системы измерения. Оценку
ее величины, обозначаемую далее через
в нормальных условиях измерения, имеет
определенный стохастический разброс.
Соответствующая дисперсия называетсядисперсией
воспроизводимости.
Она определяет точность системы как ее
внутреннее свойство, не зависящее от
характера тарировки, формы используемой
тарировочной характеристики и условий
измерения. Соответствующую доверительную
погрешность можно назвать основной
погрешностью системы измерения. Оценку
ее величины, обозначаемую далее через
![]() для ряда воздействий
для ряда воздействий![]() можно определить по формуле
можно определить по формуле

![]() ,
(7.8)
,
(7.8)
где
![]() — коэффициент Стьюдента (см. лаб. работу
№1); величина под корнем квадратным
является оценкой дисперсии воспроизводимости;
среднеарифметическое значение
— коэффициент Стьюдента (см. лаб. работу
№1); величина под корнем квадратным
является оценкой дисперсии воспроизводимости;
среднеарифметическое значение![]() вычисляется по формуле (7.3) и является
оценкой математического ожидания
выходного сигнала в нормальных условиях
измерения.
вычисляется по формуле (7.3) и является
оценкой математического ожидания
выходного сигнала в нормальных условиях
измерения.
Оценка
![]() характеризуется своей дисперсией
воспроизводимости и своей доверительной
погрешностью, которую обозначим через
характеризуется своей дисперсией
воспроизводимости и своей доверительной
погрешностью, которую обозначим через![]() .
.
По центральной
теореме математической статистики
дисперсия воспроизводимости
среднеарифметического значения
![]() в
в![]() раз меньше дисперсии воспроизводимости
сигнала
раз меньше дисперсии воспроизводимости
сигнала![]() .
Можно записать:
.
Можно записать:
![]() ,
,
![]() .
(7.9)
.
(7.9)
В данной работе
оценкой точности системы, связанной с
дисперсией воспроизводимости во всем
диапазоне измерения, служит максимальная
величина
![]() из всего ряда
из всего ряда![]() погрешностей
погрешностей![]() .
Эта оценка производится по выходному
сигналу, поэтому назовем еепределом
основной погрешности системы измерения,
приведенным к выходу системы (обычно
максимальную в диапазоне измерения
величину доверительной погрешности
называют пределом погрешности). Чаще
используются погрешности, приведенные
ко входу системы. Предел основной
погрешности системы измерения, приведенный
ко входу системы и обозначенный в
пп. 7.1.1 как
.
Эта оценка производится по выходному
сигналу, поэтому назовем еепределом
основной погрешности системы измерения,
приведенным к выходу системы (обычно
максимальную в диапазоне измерения
величину доверительной погрешности
называют пределом погрешности). Чаще
используются погрешности, приведенные
ко входу системы. Предел основной
погрешности системы измерения, приведенный
ко входу системы и обозначенный в
пп. 7.1.1 как
![]() ,
для строго или условно линейной
тарировочной характеристики определяется
по следующей формуле (для нелинейной
характеристики см. прилож. П 7.2):
,
для строго или условно линейной
тарировочной характеристики определяется
по следующей формуле (для нелинейной
характеристики см. прилож. П 7.2):
![]() .
(7.10)
.
(7.10)
В качестве
нормирующей величины для приведенных
погрешностей в данной работе используется
предел измерения
![]() .
Для приведенной
величину погрешности
.
Для приведенной
величину погрешности
![]() ,
которую обозначим через
,
которую обозначим через![]() ,
запишем:
,
запишем:
![]() .
(7.11)
.
(7.11)
Величина
![]() ,
которую следует назватьпределом
основной приведенной погрешности
системы измерения,
является наиболее удобной оценкой
точности системы как ее внутреннего
свойства, определяемого дисперсией
воспроизводимости выходного сигнала
в нормальных условиях измерения.
,
которую следует назватьпределом
основной приведенной погрешности
системы измерения,
является наиболее удобной оценкой
точности системы как ее внутреннего
свойства, определяемого дисперсией
воспроизводимости выходного сигнала
в нормальных условиях измерения.
7.1.4. Ниже
рассматривается доверительная погрешность
тарирования тензометрической измерительной
системы. Ее источниками являются
доверительные погрешности
![]() используемых эталонных воздействий
используемых эталонных воздействий![]() ,
а также доверительные погрешности
,
а также доверительные погрешности![]() определяемые по формулам (7.8), (7.9).
Данные погрешности являются погрешностями
определения точек
определяемые по формулам (7.8), (7.9).
Данные погрешности являются погрешностями
определения точек![]() исходной тарировочной характеристики
по соответствующим координатам. Суммарное
доверительное отклонение (
исходной тарировочной характеристики
по соответствующим координатам. Суммарное
доверительное отклонение (![]() )
от истинной характеристики по ее
координате
)
от истинной характеристики по ее
координате![]() в окрестности точки
в окрестности точки![]() в общем случае равно
в общем случае равно
 (7.12)
(7.12)
где
![]() — производная функции
— производная функции![]() в данной точке.
в данной точке.
Максимальное среди
всех значений
![]() отклонение является, приведенным ко
входу системы, пределом погрешности
тарировки. Обозначим его через
отклонение является, приведенным ко
входу системы, пределом погрешности
тарировки. Обозначим его через![]() .
Точность тарировки оценивается
соответствующимпределом
приведенной погрешности тарировки:
.
Точность тарировки оценивается
соответствующимпределом
приведенной погрешности тарировки:
![]() .
(7.13)
.
(7.13)
Обычно погрешность
эталонного воздействия
![]() мала
и ею можно пренебречь. Для строго и
условно линейных тарировочных
характеристик, приняв
мала
и ею можно пренебречь. Для строго и
условно линейных тарировочных
характеристик, приняв ,
из (7.12), (7.9), (7.10) и (7.11) получим
,
из (7.12), (7.9), (7.10) и (7.11) получим
![]() .
(7.14)
.
(7.14)
Для нелинейной
тарировочной характеристики расчет
значения
![]() следует
производить непосредственно по формулам
(7.12), (7.13) аналогично расчету, описанному
в прилож. П 7.2.
следует
производить непосредственно по формулам
(7.12), (7.13) аналогично расчету, описанному
в прилож. П 7.2.
7.1.5. Точность
измерений, производимых в нормальных
условиях, характеризуется пределом
основной приведенной погрешности
измерения.
В данной работе под ним понимается,
выраженная в процентах от предела
измерений, максимальная в диапазоне
измерений доверительная погрешность
измерения, выполняемого в нормальным
условиях (соответствующих условиям
тарировки). Обозначим через
![]() и
и![]() пределы основных приведенных погрешностей
измерений, выполняемых с использованием,
соответственно, исходной тарировочной
характеристики и ее линейной аппроксимации
(7.2). В первом случае для получения
результата измерения используются
выходной сигнал
пределы основных приведенных погрешностей
измерений, выполняемых с использованием,
соответственно, исходной тарировочной
характеристики и ее линейной аппроксимации
(7.2). В первом случае для получения
результата измерения используются
выходной сигнал![]() и тарировочная характеристика в табличной
или графической формах. Составляющими
погрешности
и тарировочная характеристика в табличной
или графической формах. Составляющими
погрешности![]() являются отклонение значения
являются отклонение значения![]() от его математического ожидания,
характеризуемое величиной γс, и
отклонение используемой тарировочной
характеристики от истинной, характеризуемое
величиной
от его математического ожидания,
характеризуемое величиной γс, и
отклонение используемой тарировочной
характеристики от истинной, характеризуемое
величиной ![]() .
Данные составляющие являются нормально
распределенными случайными величинами
и их доверительные значения, как
доказывается в теории вероятностей,
следует суммировать в квадратах под
корнем квадратным. Следуя этому, запишем:
.
Данные составляющие являются нормально
распределенными случайными величинами
и их доверительные значения, как
доказывается в теории вероятностей,
следует суммировать в квадратах под
корнем квадратным. Следуя этому, запишем:
![]() ,
(7.15)
,
(7.15)
где Kпр — коэффициент, учитывающий прогрессирующую погрешность, зависящую от допускаемого периода времени между тарировками.
В данной работе период времени между тарировками составляет один год и рекомендуется принять значение Kпр в интервале 1,2 ÷ 1,4.
Предел погрешности
![]() получим, если к величине
получим, если к величине![]() добавить максимальную нелинейность
тарировочной характеристики
добавить максимальную нелинейность
тарировочной характеристики![]() ,
рассмотренную в пп. 7.1.2. Причем, величину
,
рассмотренную в пп. 7.1.2. Причем, величину![]() следует рассматривать как известную
(детерминированную) систематическую
составляющую предела погрешности
следует рассматривать как известную
(детерминированную) систематическую
составляющую предела погрешности![]() .
Для определения последнего можно
записать следующее приближенное
выражение:
.
Для определения последнего можно
записать следующее приближенное
выражение:
![]() .
(7.16)
.
(7.16)
Данное выражение
завышает величину
![]() ,
так как не учитывается смещение
математического ожидания соответствующей
абсолютной погрешности от нуля на
величину нелинейности
,
так как не учитывается смещение
математического ожидания соответствующей
абсолютной погрешности от нуля на
величину нелинейности![]() .
Более точный способ приводится в прилож.
П 7.3. Отметим, что для строго линейной
тарировочной характеристики
.
Более точный способ приводится в прилож.
П 7.3. Отметим, что для строго линейной
тарировочной характеристики
![]() = 0
и
= 0
и
![]() = γос .
= γос .
7.1.6. При отличии
условий измерения от нормальных (от
условий тарировки) возникает дополнительная
погрешность.
Ее математическое ожидание, оценку
которого по выходному сигналу обозначим
через
![]() ,
является функцией измеряемого усилия
и контролируемых факторов, определяющих
условия работы измерительной системы
(прежде всего температуру и состав
среды, в которой находятся элементы
системы). Определить значения
,
является функцией измеряемого усилия
и контролируемых факторов, определяющих
условия работы измерительной системы
(прежде всего температуру и состав
среды, в которой находятся элементы
системы). Определить значения![]() можно как разность
можно как разность
![]() ,
(7.17)
,
(7.17)
где
![]() — оценки математического ожидания
выходного сигнала, полученные для ряда
эталонных воздействий
— оценки математического ожидания
выходного сигнала, полученные для ряда
эталонных воздействий![]() ,
соответственно, в нормальных условиях
и в условиях, существенно отличающихся
от нормальных, но возможных при
эксплуатации измерительной системы.
Известная функция
,
соответственно, в нормальных условиях
и в условиях, существенно отличающихся
от нормальных, но возможных при
эксплуатации измерительной системы.
Известная функция![]() часто используется как поправка к
результатам измерений, являясьсистематической
составляющей дополнительной погрешности
в контролируемых условиях измерения.
часто используется как поправка к
результатам измерений, являясьсистематической
составляющей дополнительной погрешности
в контролируемых условиях измерения.
Точность определения
величин
![]() зависит от точности контроля условий
тарировки и измерения. В зависимости
от этой точности образуетсяслучайная
составляющая дополнительной погрешности.
В данной работе рассматривается
дополнительная погрешность, связанная
с несовершенством процесса тарировки
(см. §7.4), когда принимается ускоренный
вариант последней. При этом случайная
составляющая дополнительной погрешности
проявляется в дисперсии воспроизводимости
при тарировке и учитывается пределом
основной погрешности
зависит от точности контроля условий
тарировки и измерения. В зависимости
от этой точности образуетсяслучайная
составляющая дополнительной погрешности.
В данной работе рассматривается
дополнительная погрешность, связанная
с несовершенством процесса тарировки
(см. §7.4), когда принимается ускоренный
вариант последней. При этом случайная
составляющая дополнительной погрешности
проявляется в дисперсии воспроизводимости
при тарировке и учитывается пределом
основной погрешности
![]() .
.
В настоящей работе
рассматривается также погрешность
округления младших разрядов цифровой
индикации выходного сигнала I.
Она является особым видом дополнительной
погрешности, связанной с возможной
нестабильностью этих разрядов при
измерении воздействий с ярко выраженной
стохастической природой, например, при
измерении в турбулентном потоке жидкости
(см. прилож. П 7.4). Максимум (предел)
данной погрешности достигается, как
правило, при измерении максимального
воздействия
![]() .
По погрешности округления цифрового
сигналаI
можно определить соответствующую
составляющую погрешности измерения
воздействия R,
которую будем называть просто погрешностью
округления.
Данная погрешность, как и любая другая
случайная величина, имеет случайную
составляющую с нулевым средним и
определенное математическое ожидание.
Оценку последнего можно считать
систематической составляющей погрешности
округления. Пределы
систематической и случайной составляющих
приведенной погрешности округления
обозначим через
.
По погрешности округления цифрового
сигналаI
можно определить соответствующую
составляющую погрешности измерения
воздействия R,
которую будем называть просто погрешностью
округления.
Данная погрешность, как и любая другая
случайная величина, имеет случайную
составляющую с нулевым средним и
определенное математическое ожидание.
Оценку последнего можно считать
систематической составляющей погрешности
округления. Пределы
систематической и случайной составляющих
приведенной погрешности округления
обозначим через
![]() и
и![]() .
.
Обозначим через
![]() предел
приведенной погрешности измерений
воздействия R
при
использовании тарировочной характеристики
в табличной форме. Все описанные выше
погрешности и их составляющие являются
источниками данной итоговой погрешности.
Для ее расчета можно записать следующую
приближенную формулу:
предел
приведенной погрешности измерений
воздействия R
при
использовании тарировочной характеристики
в табличной форме. Все описанные выше
погрешности и их составляющие являются
источниками данной итоговой погрешности.
Для ее расчета можно записать следующую
приближенную формулу:
![]() ,
(7.18)
,
(7.18)
где
![]() —предел
приведенной дополнительной погрешности
измерений,
—предел
приведенной дополнительной погрешности
измерений,
![]() — максимально возможное значение модуля
функции
— максимально возможное значение модуля
функции![]() .
.
Соответствующий предел абсолютной погрешности измерений равен
![]() .
(7.19)
.
(7.19)
Если используется
графическая форма тарировочной
характеристики, то возникает добавочная
графическая погрешность. Для предела
приведенной погрешности измерений,
который в данном случае обозначим через
![]() ,
можно записать следующую приближенную
формулу:
,
можно записать следующую приближенную
формулу:
![]() ,
(7.20)
,
(7.20)
где
![]() — предел
приведенной графической составляющей
погрешности измерений,
численное значение которого можно найти
в соответствии с указаниями прилож.
П 7.4.
— предел
приведенной графической составляющей
погрешности измерений,
численное значение которого можно найти
в соответствии с указаниями прилож.
П 7.4.
При использовании
линейной зависимости (7.2) для предела
приведенной погрешности измерений,
который в данном случае обозначим через
![]() ,
можно записать следующую приближенную
формулу:
,
можно записать следующую приближенную
формулу:
![]() .
(7.21)
.
(7.21)
Как отмечалось, в
данной работе погрешность
![]() образуется из-за несовершенства
ускоренного метода тарировки. Поэтому
соответствующую поправку
образуется из-за несовершенства
ускоренного метода тарировки. Поэтому
соответствующую поправку![]() целесообразно учесть непосредственно
в тарировочной характеристике путем
замены величин
целесообразно учесть непосредственно
в тарировочной характеристике путем
замены величин![]() на (
на (![]() +
+![]() ).
Если это произведено, то в (7.18), (7.20) и
(7.21) следует положить
).
Если это произведено, то в (7.18), (7.20) и
(7.21) следует положить![]() =
0.
=
0.
Систематические
погрешности, соответствующие пределам
![]() ,
,![]() ,
имеют постоянный знак во всем диапазоне
измерений рассматриваемой в данной
работе системы. Если этот знак для данных
погрешностей различен, то пределы
,
имеют постоянный знак во всем диапазоне
измерений рассматриваемой в данной
работе системы. Если этот знак для данных
погрешностей различен, то пределы![]() и
и![]() в (7.18), (7.20) и (7.21) вычитаются, если он
одинаков, то складываются. Систематическая
составляющая погрешности округления
выходного сигнала может быть учтена
как поправка при тарировке и измерениях.
Тогда в (7.18), (7.20) и (7.21) следует положить
в (7.18), (7.20) и (7.21) вычитаются, если он
одинаков, то складываются. Систематическая
составляющая погрешности округления
выходного сигнала может быть учтена
как поправка при тарировке и измерениях.
Тогда в (7.18), (7.20) и (7.21) следует положить![]() = 0.
= 0.
Формулы (7.18), (7.20),
(7.21) аналогично формуле (7.16) учитывают
систематические составляющие погрешности
![]() приближенно. Более точный их учет можно
произвести в соответствии с указаниями
прилож. П 7.3.
приближенно. Более точный их учет можно
произвести в соответствии с указаниями
прилож. П 7.3.
Цель и задачи работы
Целью работы являются приобретение навыков тарирования и определения основных метрологических характеристик тензометрических измерительных систем.
В задачи работы входят построение тарировочной характеристики тензометрической системы, определение ее нелинейности и масштаба линейной аппроксимации с обоснованием целесообразности использования этой аппроксимации, а также оценка пределов погрешности тарировки и основной погрешности измерений.
Дополнительными задачами работы, решаемыми по указанию преподавателя, являются оценки пределов цифровой погрешности округления выходного сигнала системы измерения, графической погрешности использования тарировочной характеристики и дополнительной погрешности измерений с расчетом предела погрешности измерений.
