68. Элементы релятивистской динамики. Релятивистский импульс и энергия.
Из принципа относительности следует, что математическая запись любого закона физики должна быть одинаковой во всех инерциальных системах отсчёта. Указанное условие называется условием ковариантности уравнений физических законов относительно преобразований Лоренца или, короче, условием лоренц-инвариантности.
В специальной теории относительности масса тела зависит от значения его скорости относительно инерциальной системы отсчёта
,
где m0 – масса рассматриваемого тела при υ=0. Её называют массой покоя тела, а m – массой движущегося тела или его релятивистской массой.
В релятивистской механике выполняется закон сохранения импульса: при любых процессах, происходящих в замкнутой системе, её импульс (т.е. геометрическая сумма произведений релятивистских масс всех частей этой системы на их скорости) не изменяется.
Сумма релятивистских масс соударяющихся тел до удара равна сумме их релятивистских масс после удара.
Основное уравнение релятивистской динамики имеет вид:
или
где
- импульс тела (материальной точки) в
релятивистской механике.
Скорость тела по отношению к любой инерциальной системе отсчёта не может быть равна скорости света в вакууме, а всегда меньше её.
Найдём выражение для кинетической энергии материальной точки в релятивистской механике. Приращение кинетической энергии материальной точки на элементарном перемещение dr равно работе, совершаемой на этом перемещение силой F, действующей на материальную точку: dWк=Fdr=FVdt, где V – скорость точки.
Из основного уравнения релятивистской динамики следует, что
поэтому
Так как VdV=υdυ и VV=υ2, то
С другой стороны
.
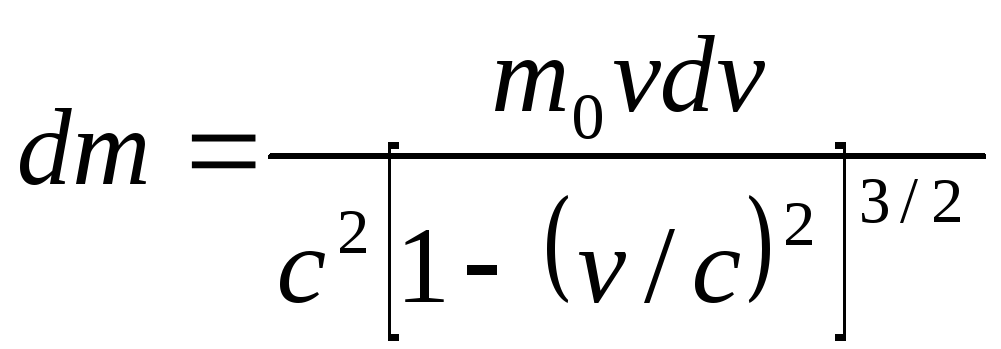Таким образом, при изменении скорости материальной точки приращения её кинетической энергии и релятивистской массы пропорциональны друг другу:
.
(68.1)
Кинетическая энергия покоящейся точки равна нулю, а её релятивистская масса равна m0. Поэтому, проинтегрировав уравнение (68.1) по m от m0 до m, получим следующее выражение для кинетической энергии материальной точки:
.