- •3.Киниматика абсолютно твердого тела. Поступательное движение твердого тела.
- •4. Принцип инерции (первый закон Ньютона). Инерциальные системы отсчета. Принцип относительности.
- •5. Преобразования Галилея.
- •6.Масса. Импульс. Сила. Второй закон Ньютона.
- •7. Сила взаимодействия. Третий закон Ньютона.
- •8.Понятие о системе тел. Внутренние и внешние силы. Вывод закона сохранения импульса. Центр инерции (центр масс) механической системы.
- •9. Работа и мощность. Работа переменной силы. Консервативные силы. Энергия кинетическая и потенциальная.
- •10Потенциальная энергия материальной точки во внешнем силовом поле. Ее связь с силой действующей на материальную точку. Понятие о градиенте скалярной функции координат.
- •Вопрос 9
- •11. Энергия кинетическая и потенциальная. Полная механическая энергия и закон ее сохранения. Примеры применения законов сохранения энергии.
- •12. Центральный удар абсолютно упругих шаров. Расчет скоростей шаров после соударения. Соударение 2х шаров с резко отличающимися массами.
- •13. Центральный удар абсолютно неупругих шаров. Расчет скоростей шаров после соударения. Соударение 2х шаров с резко отличающимися массами.
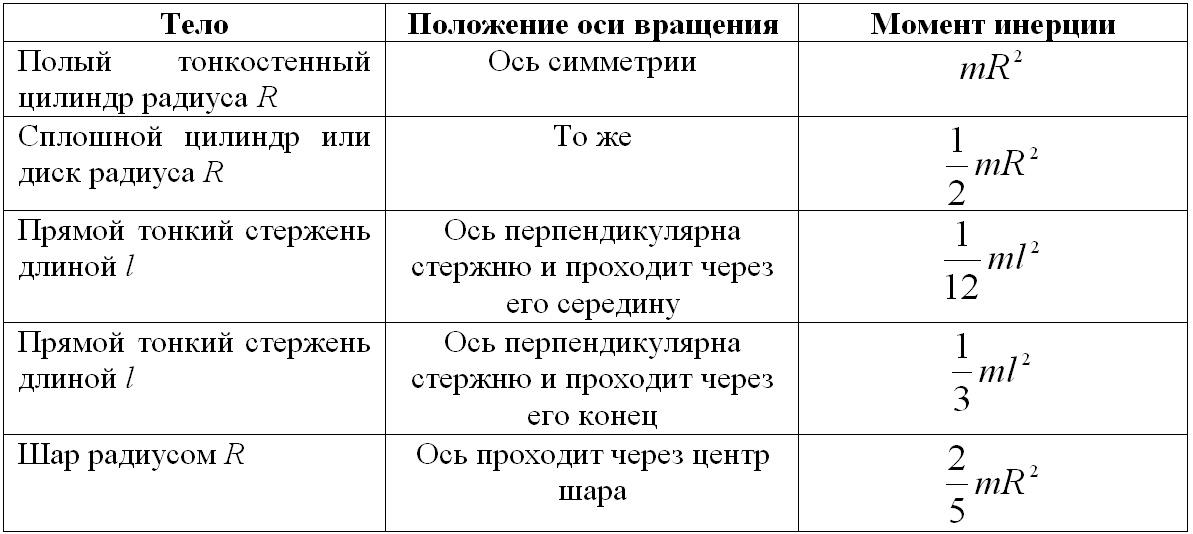
- •15.Кинетическая энергия абсолютно твердого тела, вращающегося вокруг относительно неподвижной оси. Момент инерции. Теорема Штейнера. Моменты инерции тел простейшей геометрической формы.
- •16. Вывод основного уравнения динамики вращательного движения абсолютно твердого тела. Момент импульса материальной точки и твердого тела. Закон сохранения момента импульса.
- •17. Элементы специальной теории относительности. Принцип относительности в классической механике. Преобразования Галилея. Постулаты специальной теории относительности. Преобразования Лоренца.
- •18. Релятивистская кинематика: длина тел в различных системах отсчета.
- •19.Релятивстская кинематика: длина тел и длительность событий в разных системах отсчета, релятивистский закон сложения скоростей.
- •20.Понятие о релятивистской механике. Закон взаимосвязи массы и энергии. Кинетическая энергия. Связь между полной энергией и импульсом частицы.
16. Вывод основного уравнения динамики вращательного движения абсолютно твердого тела. Момент импульса материальной точки и твердого тела. Закон сохранения момента импульса.
Момент
инерции материальной точки относительно
неподвижной оси
- скалярная физическая величина,
являющаяся мерой инертности этой точки
при вращательном движении и, равная
произведению её массы на квадрат
расстояния до оси, т.е.
![]() ,
а также
,
а также![]() ,
где
,
где![]() -
угловая скорость тела относительно
данной оси.
-
угловая скорость тела относительно
данной оси.
Теорема Штейнера: Момент инерции твердого тела относительно некоторой оси вращения равен сумме момента инерции этого тела относительно оси параллельной данной и проходящей через центр масс тел и произведению массы тела не квадрат расстояния между осями.
![]()
Обруч

Цилиндр

Круг

Стержень, ось посередине

Стержень, ось на конце
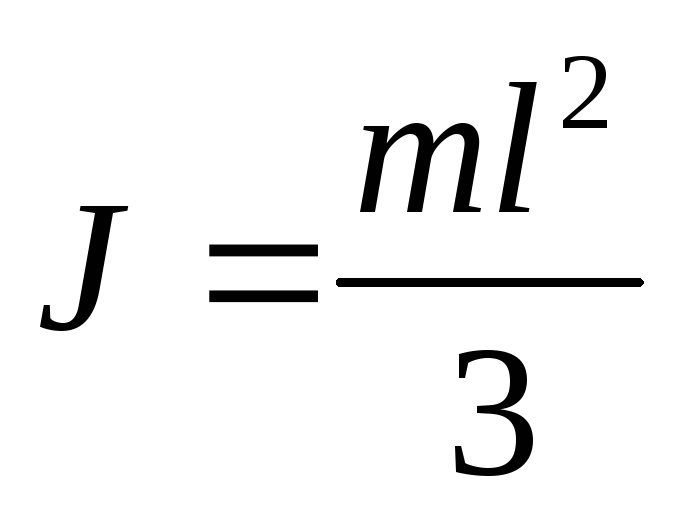
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z. При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью vi. Скорость vi и импульсmivi перпендикулярны этому радиусу, т.е. радиус является плечом вектора mivi. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:

Учитывая
связь между линейной и угловой скоростями
(vi =
ωri),
получим следующее выражение для момента
импульса тела относительно неподвижной
оси:
 (4.12)
т.е.
момент импульса твердого тела относительно
оси равен произведению момента инерции
тела относительно той же оси на угловую
скорость.
Продифференцировав
выражение (4.12) по времени,
получим:
(4.12)
т.е.
момент импульса твердого тела относительно
оси равен произведению момента инерции
тела относительно той же оси на угловую
скорость.
Продифференцировав
выражение (4.12) по времени,
получим:
 (4.13)
Это
еще одна форма уравнения динамики
вращательного движения твердого тела
относительно неподвижной оси: скорость
изменения момента импульса тела
относительно неподвижной оси вращения
равна результирующему моменту относительно
этой оси всех внешних сил, действующих
на тело.
Закон
сохранения момента импульса вытекает
из основного уравнения динамики
вращательного движения тела, закрепленного
в неподвижной точке (уравнение 4.8), и
состоит в следующем:
если
результирующий момент внешних сил
относительно неподвижной точки
тождественно равен нулю, то момент
импульса тела относительно этой точки
с течением времени не
изменяется.
Действительно,
если M =
0, то dL
/ dt =
0 ,
откуда
(4.13)
Это
еще одна форма уравнения динамики
вращательного движения твердого тела
относительно неподвижной оси: скорость
изменения момента импульса тела
относительно неподвижной оси вращения
равна результирующему моменту относительно
этой оси всех внешних сил, действующих
на тело.
Закон
сохранения момента импульса вытекает
из основного уравнения динамики
вращательного движения тела, закрепленного
в неподвижной точке (уравнение 4.8), и
состоит в следующем:
если
результирующий момент внешних сил
относительно неподвижной точки
тождественно равен нулю, то момент
импульса тела относительно этой точки
с течением времени не
изменяется.
Действительно,
если M =
0, то dL
/ dt =
0 ,
откуда
![]() (4.14)
Другими
словами, момент импульса замкнутой
системы с течением времени не
изменяется.
Из
основного закона динамики тела,
вращающегося вокруг неподвижной
оси z (уравнение
4.13), следует закон
сохранения момента импульса тела
относительно оси:
если
момент внешних сил относительно
неподвижной оси вращения тела тождественно
равен нулю, то момент импульса тела
относительно этой оси не изменяется в
процессе движения,
т.е. еслиMz =
0, то dLz /
dt =
0,
откуда
(4.14)
Другими
словами, момент импульса замкнутой
системы с течением времени не
изменяется.
Из
основного закона динамики тела,
вращающегося вокруг неподвижной
оси z (уравнение
4.13), следует закон
сохранения момента импульса тела
относительно оси:
если
момент внешних сил относительно
неподвижной оси вращения тела тождественно
равен нулю, то момент импульса тела
относительно этой оси не изменяется в
процессе движения,
т.е. еслиMz =
0, то dLz /
dt =
0,
откуда
![]() (4.15)
Закон
сохранения момента импульса является
фундаментальным законом природы.
Справедливость этого закона обусловливается
свойством симметрии пространства –
его изотропностью, т.е. с инвариантностью
физических законов относительно выбора
направления осей координат системы
отсчета.
Справедливость
закона сохранения момента импульса
относительно неподвижной оси вращения
можно продемонстрировать на опыте со
скамьей Жуковского. Скамьей Жуковского
называется горизонтальная площадка,
свободно вращающаяся без трения вокруг
неподвижной вертикальной оси ОО1.
Человек, стоящий или сидящий на скамье,
держит в вытянутых руках гимнастические
гантели и приводится во вращение вместе
со скамьей вокруг оси ОО1 с
угловой скоростью ω1.
Приближая гантели к себе, человек
уменьшает момент инерции системы, а так
как момент внешних сил равен нулю, момент
импульса системы сохраняется и угловая
скорость ее вращения ω2 возрастает.
Тогда по закону сохранения момента
импульса относительно оси ОО1 можно
записать:
(4.15)
Закон
сохранения момента импульса является
фундаментальным законом природы.
Справедливость этого закона обусловливается
свойством симметрии пространства –
его изотропностью, т.е. с инвариантностью
физических законов относительно выбора
направления осей координат системы
отсчета.
Справедливость
закона сохранения момента импульса
относительно неподвижной оси вращения
можно продемонстрировать на опыте со
скамьей Жуковского. Скамьей Жуковского
называется горизонтальная площадка,
свободно вращающаяся без трения вокруг
неподвижной вертикальной оси ОО1.
Человек, стоящий или сидящий на скамье,
держит в вытянутых руках гимнастические
гантели и приводится во вращение вместе
со скамьей вокруг оси ОО1 с
угловой скоростью ω1.
Приближая гантели к себе, человек
уменьшает момент инерции системы, а так
как момент внешних сил равен нулю, момент
импульса системы сохраняется и угловая
скорость ее вращения ω2 возрастает.
Тогда по закону сохранения момента
импульса относительно оси ОО1 можно
записать:
![]() (4.16)
где J0 -
момент инерции человека и скамьи; 2mr12 и
2mr22 -
моменты инерции гантелей в первом и
втором положениях; m –
масса одной гантели; r1, r2 –
расстояния от гантелей до оси
ОО1.
Изменение
момента инерции системы связано с
изменением ее кинетической энергии:
(4.16)
где J0 -
момент инерции человека и скамьи; 2mr12 и
2mr22 -
моменты инерции гантелей в первом и
втором положениях; m –
масса одной гантели; r1, r2 –
расстояния от гантелей до оси
ОО1.
Изменение
момента инерции системы связано с
изменением ее кинетической энергии:

Используя выражение для ω2, полученное из (4.16)

после преобразований получим:

Это изменение кинетической энергии системы численно равно работе, совершенной человеком при перемещении гантелей. В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.
Таблица 4.2