15.Кинетическая энергия абсолютно твердого тела, вращающегося вокруг относительно неподвижной оси. Момент инерции. Теорема Штейнера. Моменты инерции тел простейшей геометрической формы.

Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси.

Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m₁, m₂,…,m_n, находящиеся на расстоянии r₁, r₂,…, r_n, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусов r_i и имеют различные линейные скорости υ_i.

Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т₁, т₂ ,..., т_n , находящиеся на расстоянии r₁, r₂,..., r_n от оси.

При вращении твердого тела относительно неподвижной оси отдельные его элементар­ные объемы массами m_i опишут окружности различных радиусов r_i, и имеют различные линейные скорости v_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:

(17.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

или

Используя выражение (17.1), получаем

где J_z — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела

(17.2)

Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv²/2), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси.

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

где m — масса катящегося тела; v_c — скорость центра масс тела; Jc — момент инер­ции тела относительно оси, проходящей через его центр масс;  — угловая скорость тела.

Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов.

T_вр=∑ⁿ_i=1m_iυ_i²/2=∑ⁿ_i=1m_iω²r_i²/2=(ω²∑ⁿ_i=1m_ir_i²)/2=I_zω²/2, гдеI_z – момент инерции тела. Вращение твёрдого тела вокруг неподвижной оси:

Можно показать, что проекция момента импульса на ось “Z” может быть записана таким образом:

где R – расстояние до оси.

Момент инерции материальной точки относительно неподвижной оси - скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также, где- угловая скорость тела относительно данной оси.

Теорема Штейнера: Момент инерции твердого тела относительно некоторой оси вращения равен сумме момента инерции этого тела относительно оси параллельной данной и проходящей через центр масс тел и произведению массы тела не квадрат расстояния между осями.

• Обруч

• Цилиндр

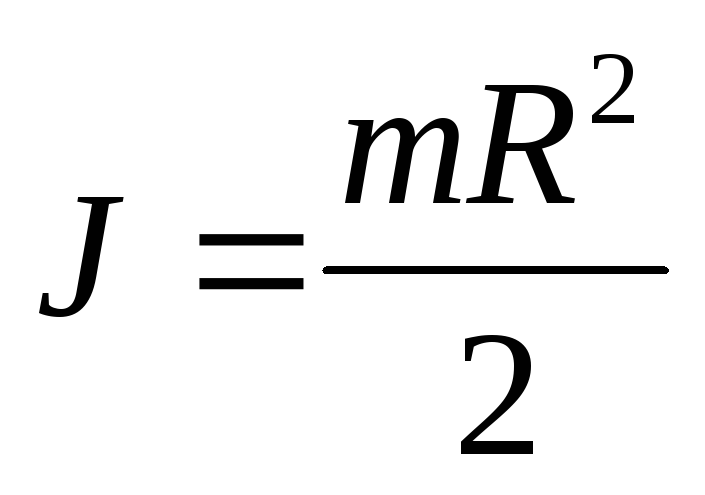
• Круг

• Стержень, ось посередине

• Стержень, ось на конце