7. Сила взаимодействия. Третий закон Ньютона.

В механике большое значение имеет принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач.

Если на материальную точку действуют одновременно несколько сил, то, согласно принципу независимости действия сил, под силой во втором законе Ньютона понимают результирующую силу.

Виды сил:

Гравитационные силы, электромагнитные силы, силы инерции, ядерные силы, силы межмолекулярного взаимодействия.

В физике существует 4 фундаментальных взаимодействия:

• Гравитационное

• Электромагнитное

• Сильное (ядерное)

• Слабое (распад элементарных частиц)

Воздействие тел (материальных точек) друг на друга всегда является взаимным и определяется третьим законом Ньютона (законом о равенстве действия и противодействия): действия двух тел друг на друга всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела:                                                                                                         (2.7) где F₁₂ - сила, действующая на первое тело со стороны второго; F₂₁ - сила, действующая на второе тело со стороны первого.       Необходимо помнить, что силы F₁₂ и F₂₁ приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.       Примеры, иллюстрирующие третий закон Ньютона:       1) Человек прыгает с лодки на берег. Он толкает лодку назад с силой F₁₂, а сам испытывает со стороны лодки силу F₂₁, направленную в сторону, противоположную направлению F₁₂. Поэтому человек и лодка движутся в прямо противоположных направлениях.       2) Камень массой m падает с обрыва на Землю с ускорением g. Он притягивается к Земле с такой же по величине силой, что и Земля к камню. Просто мы не замечаем движения Земли, т.к. ее масса Мво много раз превышает массу m камня, следовательно, ускорение a, с которым движется Земля, ничтожно мало по сравнению с ускорением g. В самом деле, с учетом второго закона Ньютона уравнение (2.7) запишется в виде:

• 

откуда

• 

      Заменим в уравнении (2.7) силы F₁₂ и F₂₁ согласно формуле (2.5):

• 

      Тогда

• 

• или                                                                                     (2.8)       Следовательно, при механическом взаимодействии двух тел изменения их импульсов численно равно и противоположны по направлению.       Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

8.Понятие о системе тел. Внутренние и внешние силы. Вывод закона сохранения импульса. Центр инерции (центр масс) механической системы.

Силы, действующие на тело (или систему тел), делятся на внешние и внутренние. Внутренние силы возникают в теле под действием внешних сил.

Совокупность сил, действующих на какое-либо тело, называют системой сил.

Эквивалентная система сил — система сил, действующая так же, как заданная.

Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.

Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.

Механической системой тел – называется совокупность материальных точек (тел), рассматриваемых как единое целое.

Внешние силы - это силы, действующие на систему со стороны внешних тел. Внешние тела - это тела не входящие в систему.

Внутренние силы - это силы, взаимодействующие между частями рассматриваемой системы.

Закон сохранения импульса: Вектор полного импульса замкнутой системы тел с течением времени не меняется.

Вывод закона:

Пусть система состоит из n материальных точек, массы которых m1, m2,…mn, а скорости V1,V2…Vn. Для них:

2ЗН (m1): (d/dt) m1V1 = F1,2 +F1,3 + … F1,n;

2ЗН (m2): (d/dt) m2V2 = F2,1 + F2,3 + …F2,n;

2ЗН (mn): (d/dt) mnVn = Fn1 + Fn2 + …Fn (n-1).

По третьему закону Ньютона: Fik = Fki (*)

Сложим уравнение (А) с учетом уравнения(*):

;

Из закона сохранения импульса следует, сто при любых процессах происходящих в замкнутой системе скорость её центра инерции – это постоянный вектор. Замкнутых механических систем не существует в природе, но, не смотря на это в ряде случаев законом сохранения импульса пользоваться можно:

1. Сумма всех внешних сил равна нулю.

2. Удаётся найти такое направление, на которое проекция всех внешних сил в сумме дают ноль. Тогда для этой оси можно использовать закон сохранения импульса.

3. Быстро текущие процессы: взрыв, удар, выстрел, …

Центр инерции (центром масс) системы – такая геометрическая точка, которую можно выделить в любой механической системе, движение которой определяется внешними силами, действующими на систему и массой всей механической системы.

Центром масс системы материальных точек называется точка С, радиус-вектор которой равен:

, где -масса и радиус-вектор «i-ой» точки

- масса всей системы.

 Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен

где 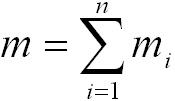 масса системы.       Скорость центра масс определяется выражением:

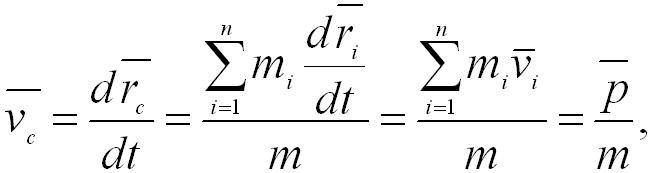
т.е.                                                                                                                (2.10)       Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции.       Подставив выражение (2.10) в (2.9), получим:

      т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно.       Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом:

или                                                                                                                (2.11) где  ускорение центра масс.       Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.