Вопрос 42. Физический и математический маятники. Периоды их колебаний. Приведенная длина физического маятника.

1. Математический маятник – модель состоит из материальной точки подвешенной не длине невесомой и нерастяжимой нити совершающей колебания в вертикальной плоскости под действием силы тяжести.

При движении материальной точки совершается вращательное

движение относительно оси проходящей через точку подвеса О.

Так как линия действующего натяжения нити проходит через ось

вращения то ее момент относительно оси равен 0.

На Ох: . При малых углах отклонения от вертикали,можно считать чтоsinα≈α.

Решением этого уравнения является функция вида: - математический маятник совершает колебания по гармоническому закону.-период колебания математического маятника не зависит от массы маятника, а зависит от его длины и ускорения свободного падения в том месте где подвешен маятник.

2. Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. Считая колебания малыми положим чтоsinφ=φ, тогда - дифференциальное уравнение гармонических колебаний решением которого является.Период физического маятника.Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.  или

Из этого соотношения определяем . Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

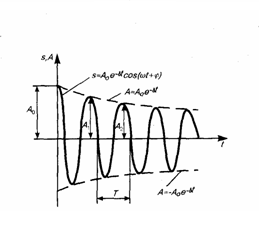
Вопрос 43. Затухающие колебания. Дифференциальное уравнение затух колеб и его решение. Логарифмический дискремент и коэффициет затухания. Затухающие колебания – это колебания, амплитуда которых из-за потерь энергии реальной колебательной системы с течением времени уменьшается. Дифференциальное уравнение свободно затухающих колебаний линейной системы задаётся в виде:

, где х – колеблющаяся величина, описывающая тот или иной физический процесс, β=b/2m=const – коэффициент затухания, ω₀ – циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при β =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение дифференциального уравнения затухающих элементов:

Сделаем

Подставляем найденное вместе с выражением для х и после сокращения на . 1)Еслито решение этого Д/У имеет вид. Начальная амплитуда колебаний А и начальная фаза φ зависит от способа возбуждения колебаний. Решением этого уравнения являются затухающие колебания. Периодом затухающих колебаний называется промежуток времени между двумя последними выражениями колебательной системы от положения равновесия. ЕслиA(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение: называется декрементом затухания, а его логарифм

- логарифмическим декрементом затухания; N_e – число колебаний, совершаемых за время уменьшения амплитуды в e раз. Логарифмический декремент затухания – постоянная для каждой колебательной системы величина. 2) если - в этом случае понятие периода теряет смысл- апериодический характер.